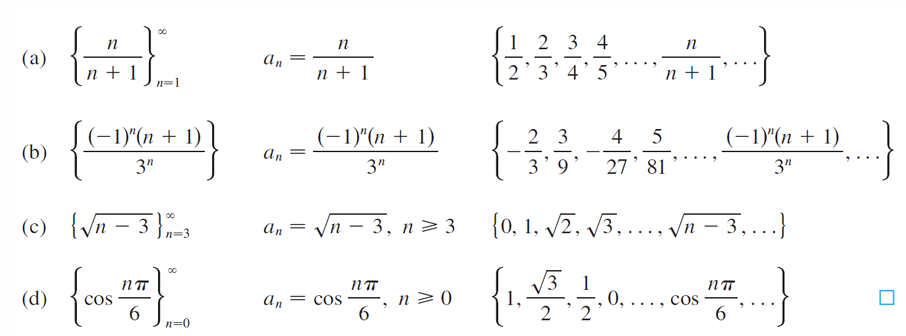应用

泰勒公式解决的问题：找到一个多项式函数(幂函数)在某个范围内等价复杂的函数

”某个范围“

要找到一个函数和原函数值在定义域内性质全部相同很困难，所以我们考虑找到一个函数在某个区间内性质能够完全与原函数相同就够了。其实包括之前的等价无穷小，那些找到用来近似(注意不是等价)原函数的函数也只是在x->0即0附近的区间才成立

”等价“

注意泰勒公式是一个等式，是用=而不是~连接的，泰勒（和麦克劳林公式）展开的项数越多，近似的精确度就越高，等价无穷小(近似)就是泰勒公式的阉割版,因为近似只做到一阶导(有限阶导）与原函数相同，而泰勒找到的这个函数在n阶导都与原函数相同，当然也带来了一个新的问题：等价原函数的函数需要精确到几阶导

”复杂的函数”

e^0.001这种奇怪的指数函数你肯定不好算，但如果转化成一个等价的多项式函数。由于它本身的运算仅是有限项加减法和乘法，所以在数值计算方面，多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。

• 近似在高次参数时比降次便捷

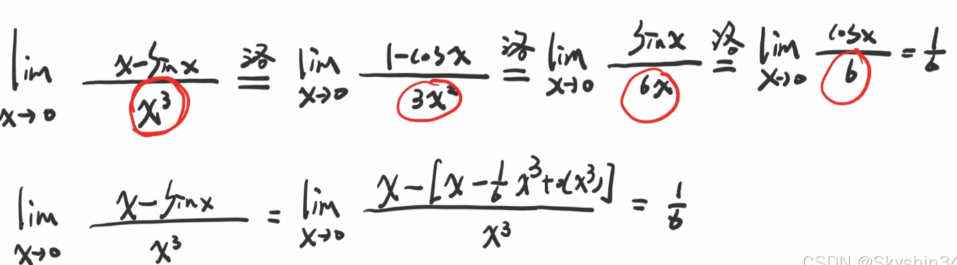
洛必达的本质是降阶，泰勒公式的本质是近似，等价无穷小是特殊的泰勒公式

公式

单元函数的泰勒展开式

称为f在\(x_0\)处的n次泰勒多项式

• 麦克劳林公式是泰勒公式的一种特殊情况，即当x0=0时的泰勒公式
• 余项：展开式与原函数的差

泰勒级数的表示

$$f ( x ) = \sum _ { n = 0 } ^ { \infty } \frac { f ^ { ( n ) } ( a ) } { n ! } ( x – a ) ^ { n }$$

多元函数的泰勒展开式

证明函数完全展开为麦克劳林级数和：

当函数 \( f(x) \) 的泰勒多项式 \( T_n(x) \) 的余项 \( R_n(x) \) 满足
\[
\lim_{n \to \infty} R_n(x) = 0
\]
（对于 \( |x – a| < R \)），则 \( f(x) \) 在该区间内等于其泰勒级数的和。

在尝试证明某个特定函数 \( f \) 满足 \(\lim_{n \to \infty} R_n(x) = 0\) 时，通常需要以下关键工具

泰勒不等式：若对于满足 \(|x – a| \leq d\) 的所有 \( x \)，有 \(|f^{(n+1)}(x)| \leq M\)，则泰勒级数的余项 \(R_n(x)\) 满足不等式
\[|R_n(x)| \leq \frac{M}{(n+1)!}|x – a|^{n+1}\]在区间 \(|x – a| \leq d\) 内成立。

在应用上2个定理时，以下结论非常有用：

\[\lim_{n \to \infty} \frac{x^n}{n!} = 0\]

对任意实数 \( x \) 成立。因为已知级数 \(\sum \frac{x^n}{n!}\) 对所有 \( x \) 收敛（参考例1），因此其第 \( n \) 项必然趋近于零。

e^x

收敛半径即看敛散性，看到阶乘直接用比较法判断敛散性

要证明一个函数能完全等价泰勒级数，需要函数单调 / 有上下限 ，比如/(e^x/)和正余弦函数，否则无法满足泰勒不等式的条件（见上）

sin cos

\[
\sin x = x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!} + \cdots = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!} \quad \text{for all } x
\]\[
\cos x = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \frac{x^6}{6!} + \cdots= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!} \quad \text{for all } x
\]

(1+x)^x

泰勒级数与二项式系数

传统二项式系数是广义二项式系数在 k为正整数时的特例。前者仅用于有限展开，后者支持无限级数展开，适用于更广泛的数学分析。阶乘只能用于正整数

利用泰勒级数计算反常积分的导数

评估泰勒级数近似函数时的误差

在泰勒多项式中，余项 \( R_n(x) \) 的下标 \( n \) 表示对应的泰勒多项式 \( T_n(x) \) 的阶数（即最高次项为 \((x-a)^n\)）。对于二阶泰勒多项式 \( T_2(x) \)，其误差余项为 \( R_2(x) \)，因此泰勒不等式中的余项符号为 \( R_2 \)。公式中涉及的三阶导数（\( n+1=3 \)）是因为泰勒不等式需要用到更高一阶的导数来估计余项的界。

推导思路（不严格）

我们发现多项式幂函数 三阶导 在0附近的结果只与对应的幂的项有关，比该幂小的项在求导的过程中被导为0，而高阶导因为代入X0=0后所以为0。同理我们能发现该例子中四阶导的结果为7 4！,这很好理解，首先7作为常数项在求导过程中一直不变，而x^4在经历次求导的结果即为4！

所以我们发现一个性质，多项式幂函数，n次幂项决定n阶导的结果

e^x求导结果不变又因为设定区间在0附近，因此n阶导的结果都是1，所以得到

PS：我发现利用e^xN阶导数不变的性质能推导很多重要的性质，欧拉公式中也是利用e^x求导不变性得到的复平面单位圆。

首先0次项决定的是图像整体的上下偏移，e^x(0) =1所以a=1。

但如果设定区间规定为x=a附近而不是0的话，多项式的高次项不在因为x0=0而消去，因此我们添加一个（x-x0），这样就使这个多项式幂函数在X0≠0时也能具有“n次幂项决定n阶导的结果”的性质

根据该性质我们写出原函数导函数与多项式各项系数的关系，然后将其代入到多项式中，就能得到泰勒公式了

题目

用下面一个例题来解释上述三点

1.乘除位置使用等价无穷小，任意位置可用泰勒展开式。

AEF左右都是乘法可以用等价无穷小，B和cd是减法，需要考虑展开只取前两项（等价无穷小）是否足够精确

2.上面是1阶，下面是3阶，不能只取前一项近似（不能用等价无穷小近似）所以必须要展开到同阶才能近似，忽略高阶量因为太小忽略不影响近似