用于统计计算和图形的编程语言和环境。广泛用于数据分析和统计建模，R是DS最流行的一种解释语言，开源，有很多免费的包可以添加。

语法

运算符

# R中的基本算术运算
a <- 5

sum_result <- a + b  # 加法
diff_result <- a - b  # 减法
prod_result <- a * b  # 乘法
quot_result <- a / b  # 除法
# 这些操作的结果存储在变量sum_result、diff_result、prod_result和quot_result中

%in%运算符用于检查元素是否存在于向量中。它返回TRUE或FALSE
x <- c(1, 2, 3, 4, 5)
result <- 3 %in% x  # 检查3是否在x中

向量和赋值

# 使用c()函数创建向量
v <- c(1, 2, 3, 4, 5)  # 数值向量
names(v) <- c("a", "b", "c", "d", "e")  # 为元素分配名称

# 通过索引或名称访问单个元素
v[1] 
v["c"] 

数据类型

# R中的数据类型
num_var <- 42  # 数值型变量
char_var <- "Hello R"  # 字符型变量
logical_var <- TRUE  # 逻辑型变量
# 数据框：数据表，通常用于存储数据集

常用内置函数

x <- c(1, 2, 3, 4, 5)
y <- matrix(1:9, nrow = 3, ncol = 3)
df <- data.frame(A = 1:5, B = 6:10)

# 均值、中位数和标准差
mean(x)  # 计算x的均值
median(x)  # 计算x的中位数
sd(x)  # 计算x的标准差

# 和与积
sum(x)  # x中元素的和
prod(x)  # x中元素的积

# 对象的大小和维度
length(x)  # x中元素的数量
dim(y)  # 返回矩阵的维度
nrow(df)  # 返回数据框或矩阵的行数
ncol(df)  # 返回数据框或矩阵的列数

# 使用which()查找索引
which(x %% 2 == 0)  # x中偶数的索引

# 对向量进行排序
sort(x)  # 按递增顺序排序x
order(x)  # 获取排序x的索引

# 频率表
x <- c("apple", "banana", "apple", "orange", "banana", "banana")
table(x)  # 创建一个频率表，用于计算向量中每个唯一值的出现次数

# 重复和序列
rep(1:3, times = 2)  # 重复向量的元素,重复向量1:3，两次 //[1] 1 2 3 1 2 3
seq(1, 10, by = 2)  # 生成数字序列,生成从1到10的序列，步长为2

# 使用setdiff()查找两个集合的差异
A <- c(1, 2, 3, 4)
B <- c(3, 4, 5, 6)

setdiff(A, B)  # 在A中但不在B中的元素
union(A, B)  # A和B的并集
intersect(A, B)  # A和B的交集

#从给定向量或一组数字中随机抽取样本。您可以有放回或无放回地抽样
sample(1:10, 5)  # 从1到10中抽取5个数字
sample(1:10, 5, replace = TRUE)  # 有放回抽样

# 使用hist()绘制直方图
data <- c(1, 2, 2, 3, 4, 4, 4, 5, 6, 6)
hist(data, breaks=6, col="lightblue", main="Histogram Example", xlab="Value")
// data输入数据，通常是一个数值向量；breaks 参数用于指定直方图的区间（bin）数量或区间边界
//col 参数用于设置直方图的填充颜色；main 参数用于设置图表的标题；xlab 参数用于设置 x 轴的标签
//ylab 参数用于设置 y 轴的标签；border 参数用于设置直方图条形的边框颜色

文件操作

不建议通过RStudio中的页面按钮导入数据文件(.csv)，而是通过编码的方式导入，这样会更容易配置，并且整个过程是自动完成的

#读取文件
my_data <- read.csv("文件名")

#安装package
install.packages("packageName") //只需要安装一次

#引用包
library("packageName") //可以访问包内扩展的命令
#引用数据集
data("dataSeriesName")

# 查看数据
head(my_data) //输出前6行数据
tail(my_data) //控制台输出最后6行数据
view(my_data) //查看所有数据，也可通过点击环境面板中的存储数据的变量查看

#提取特定数据
my_data[1,3] //引用[行，列]中的数据
my_data[ ,3] //引用第3列所有行中的数据
my_data$variableName //引用该名称指向的所有数据

应用

事件概率计算

# 定义六面骰子的样本空间
omega <- c(1, 2, 3, 4, 5, 6)
# 定义得到奇数的事件
A <- c(1, 3, 5)

# 每个结果的概率为1/6
probability <- rep(1/6, 6)

# 为概率值分配名称,names接受一个向量
names(probability) <- omega

# 计算事件A（奇数）的概率
# 奇数结果的概率之和
P_A <- sum(probability[omega %in% A])
# omega %in% A 会返回一个逻辑向量:TRUE,FALSE,TRUE,FALSE,TRUE,FALSE表示 A 中的每个元素是否在 omega中
#probability[omega %in% A] 会提取 probability 中对应 TRUE 的元素，即 1/6,1/6,1/6。
#sum(probability[omega %in% A]) 会计算这些概率的和，即 3×1/6 = 1/2。
最终，P_A 被赋值为0.5

# A的补集：不在A中的结果
Ac <- setdiff(omega, A) //[1] 2 4 6

# 定义事件B：掷出小于3的数
B <- c(1, 2)

# A和B的并集
union_A_B <- union(A, B) //[1] 1 2 3 5

# A和B的交集
intersection_A_B <- intersect(A, B) //[1] 1

模拟掷骰子

# 模拟掷两个骰子1000次
set.seed(123)  # 为了可重复性
dice_rolls <- sample(1:6, 1000, replace=TRUE) + sample(1:6, 1000, replace=TRUE)

# 绘制和的分布
hist(dice_rolls, breaks=11, col="lightblue", main="Distribution of Sums of Two Dice Rolls", xlab="Sum", ylab="Frequency", border="black")

ggplot2

用于创建优雅且可自定义的可视化，提供了一种结构化的方式来用最少的代码创建复杂的图形。ggplot2可视化的基本结构如下：

ggplot(data)+aes(x, y)+geom()+theme()

• ggplot(data)：指定用于绘图的数据集
• aes(x, y)：将数据集中的变量与图形的视觉属性关联起来，x 和 y表示映射到x轴和y轴的变量。可以在aes中包含其他美学映射color, fill, size, shape, and alpha (transparency)
• geom()：指定用于可视化的几何对象类型：geom_point() – scatter plot散点图；geom_line() – line plot折线图；geom.histogram() – histograms直方图；geom_boxplot() – box plot箱线图；geom_density() – density plot密度图
• theme()：控制图形的外观：theme_classic() – 简洁的背景和干净的线条；theme_bw() – 黑白主题，带有网格线；theme_minimal() – 移除背景元素
• labs()：用于为图形添加标签和标题

 labs(title="Plot Title", x="X-Axis Label", y="Y-Axis Label")

• scale_color_manual() 和 scale_fill_manual()：允许为离散变量自定义颜色
• facet_wrap() 和 facet_grid()：用于基于分类变量创建多个子图

直方图 Histograms

将数据范围划分为kk个区间并计算每个区间内的观测数量来近似数据集的分布

上面的模拟抛骰子用R的Base库实现，这里用ggplot2包实现

 library(ggplot2)
 # Create a histogram with ggplot2
 ggplot(data = mtcars, aes(x = mpg)) +
 geom_histogram(bins=10, fill="lightblue", color="black") +labs(title="Distribution of Miles Per Gallon", x="Miles PerGallon", y="Frequency") +theme_classic()

箱线图Box Plot

总结了中位数、四分位数和潜在异常值等关键统计量。箱线图特别适用于比较不同类别的分布

箱线图由以下部分组成：

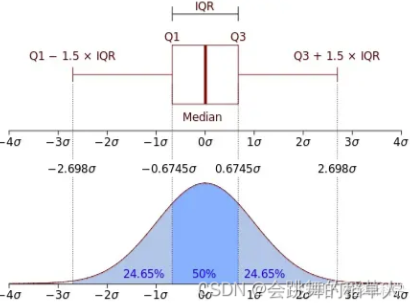
• 四分位数：共有三个，从小到大分别用Q1、Q2、Q3表示
• 箱体Box：表示Q1与Q3的差距又称四分位距（IQR），涵盖数据的中间50%。\( IQR = Q_3 – Q_1 \)
• 中位数median：数据集中间的值即Q2，显示为箱体内部的一条线
• 须线（Whiskers）：从箱体延伸出去的线，通常延伸到四分位数的1.5倍IQR范围内的最小和最大观测值。下须线 \( = Q_1 – 1.5 \times IQR\) \(上须线 ( = Q_3 + 1.5 \times IQR )\)
• 异常值（Outliers）：超出须线的单个数据点。

分位数是将总体的全部数据按大小顺序排列后，处于各等分位置的变量值。如果将全部数据分成相等的两部分，它就是中位数；如果分成四等分，其中每部分包括25%的数据，就是四分位数；八等分就是八分位数等，四分位数的数学表示

\[ Q_1 = X_{\left\lfloor \frac{n+1}{4} \right\rfloor}, \quad Q_3 = X_{\left\lfloor \frac{3(n+1)}{4} \right\rfloor} \]

• \(X_i\) 表示有序数据集中的第 i个最小值。
• \(i \)是排序数据集中元素的索引。
• \(n\) 是数据集中的总观测数。
• \(\lfloor \cdot \rfloor\) 表示向下取整函数，将数字向下舍入到最接近的整数。

 # Load dataset
 data(mtcars)
 
 # Create a box plot of mpg grouped by number of cylinders
 boxplot(mpg ~ as.factor(cyl), data = mtcars, col="lightblue",main="Miles Per Gallon by Number of Cylinders",xlab="Number of Cylinders", ylab="Miles Per Gallon")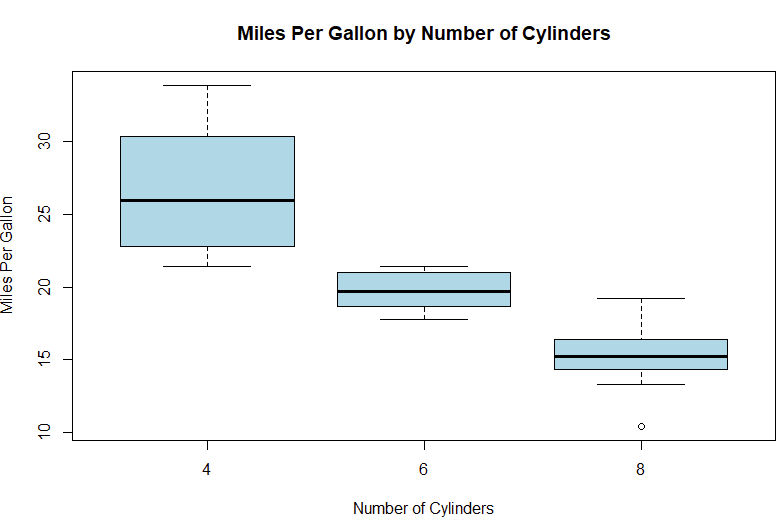

library(ggplot2)

# Create a box plot using ggplot2
ggplot(data = mtcars, aes(x = as.factor(cyl), y = mpg, fill = as.
factor(cyl))) +
geom_boxplot() +
labs(title=”Miles Per Gallon by Number of Cylinders”,x=”Number of Cylinders”, y=”Miles Per Gallon”) +
theme_classic() +
scale_fill_manual(values=c(“lightblue”, “lightgreen”, “lightcoral”))

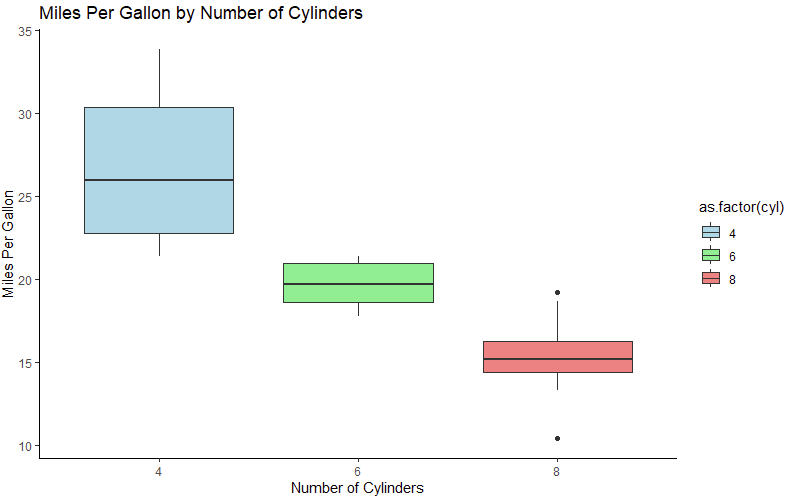
密度图 Density Plot

密度图是直方图的平滑版本，表示连续随机变量的概率密度函数（PDF）。与使用离散区间的直方图不同，密度图使用核密度估计（KDE）来估计分布，提供一条连续的曲线。

$$ P(a \leq X \leq b) = \int_a^b f(x) \, dx $$

其中 ( f(x) ) 是满足以下条件的密度函数：

$$ \int_{-\infty}^{\infty} f(x) \, dx = 1 $$

密度图提供了 ( f(x) ) 的非参数估计，通常使用核密度估计（KDE），它使用核函数 ( K ) 和带宽参数 ( h ) 来平滑数据。点 ( x ) 处的估计密度为：

$$ \hat{f}(x) = \frac{1}{nh} \sum_{i=1}^n K \left( \frac{x – X_i}{h} \right) $$

其中：

• f^(x)：符号 ^（读作“hat”）通常用来表示估计量或估计值，对密度函数 f(x) 的估计
• \(X_i \) 表示第 i 个样本数据点
• n 是总观测数。增加 n 会导致更可靠的密度估计，减少变异性
• \( K(\cdot) \) 是核函数（例如高斯核）。核函数通过对每个数据点进行加权，生成一个平滑的密度估计，不同的核函数会影响密度估计的平滑度，其影响通常比带宽小
• h是带宽 bandwidth，控制估计的平滑度：较小的 h 会导致更敏感的估计，捕捉更精细的细节，但可能导致过拟合（高方差、锯齿状外观）。较大的 h 通过减少波动产生更平滑的估计，但可能会过度平滑数据并掩盖重要特征（高偏差）

# Load dataset
data(mtcars)

# Compute and plot the density of Miles Per Gallon (mpg)
plot(density(mtcars$mpg), col="blue", lwd=2,
main="Density Plot of Miles Per Gallon",
xlab="Miles Per Gallon", ylab="Density")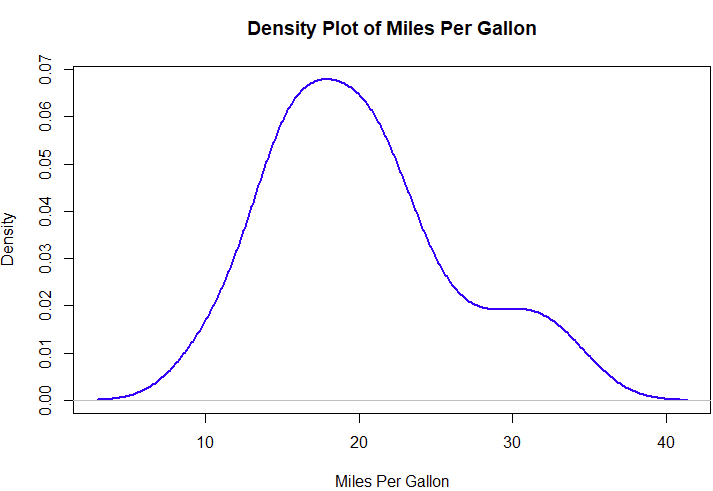

library(ggplot2)

# Create a density plot using ggplot2
ggplot(data = mtcars, aes(x = mpg)) +
geom_density(fill="lightblue", color="black", alpha=0.5) +
labs(title="Kernel Density Estimate of Miles Per Gallon", x="Miles Per Gallon", y="Density") + theme_classic()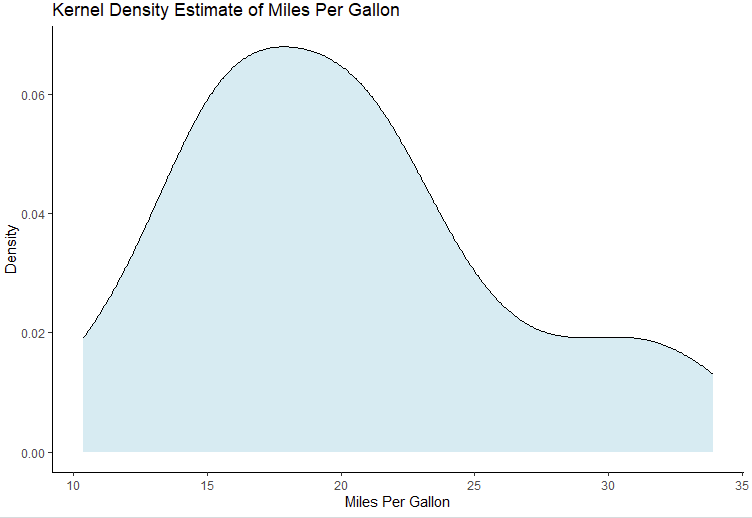

Stem-and-LeafPlots 茎叶图

一种显示数值数据同时保留原始值的方法。对于以下方面非常有用：识别集中趋势（值集中的位置），检测分布的偏斜或对称性，识别数据中的异常值或间隙

茎叶图将每个数据值分为：茎表示前导数字（例如，十位）。叶表示尾随数字（例如，个位）

例如，给定数字23,25,27,32,35茎叶图将为：2 | 357 3 | 25

在R中创建茎叶图，使用内置的stem()函数：

# Sample dataset
data <- c(23, 25, 27, 32, 35, 40, 42, 45, 47, 50, 53, 55)
 
# Create a stem-and-leaf plot
cat("Stem-and-Leaf Plot:\n")
stem(data)
 
# Create a histogram for comparison
hist(data, col="lightblue", breaks=5,
main="Histogram of Data", xlab="Value", ylab="Frequency",border="black")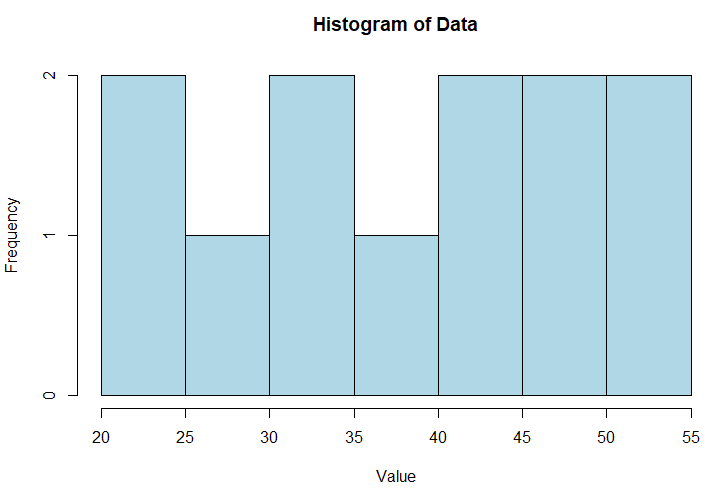

2 | 357
3 | 25
4 | 0257
5 | 035

Faceting:Multiple Subplots 分面 多个子视图

library(ggplot2)

# Faceted histogram of mpg by cylinder count
ggplot(data = mtcars, aes(x = mpg)) +
geom_histogram(bins=10, fill="lightblue", color="black") +
facet_wrap(~ cyl) +labs(title="Histogram of MPG by Number of Cylinders",x="Miles Per Gallon", y="Frequency") +theme_classic()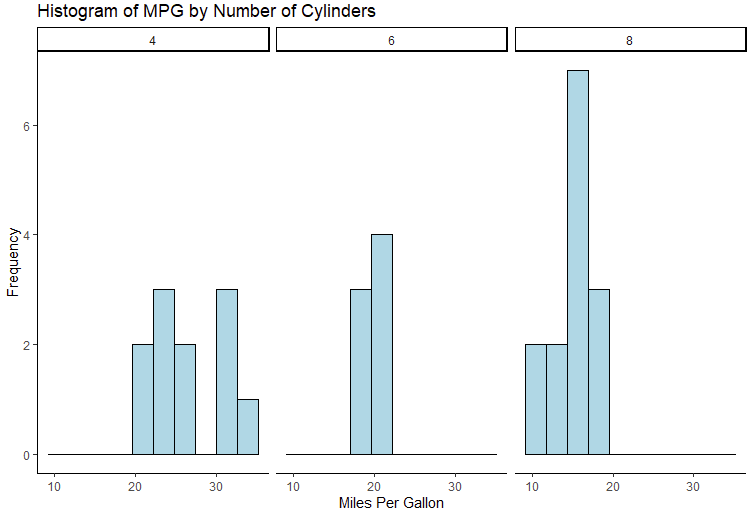

library(ggplot2)

# Faceted density plot of mpg by cylinders and transmission type
ggplot(data = mtcars, aes(x = mpg, fill = as.factor(cyl))) +
geom_density(alpha=0.5) +
facet_grid(am ~ cyl) +
labs(title="Density Plot of MPG by Cylinders and Transmission
Type",x="Miles Per Gallon", y="Density") +theme_classic()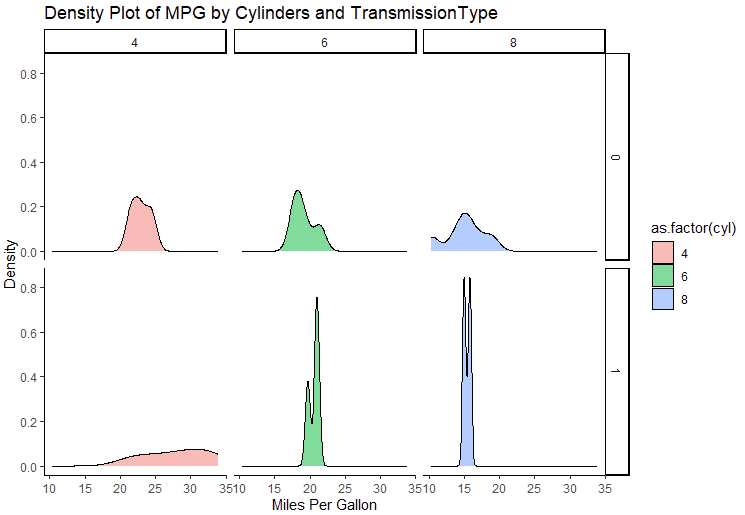

facet_grid(am ~ cyl) 表示根据 am 和 cyl 两个变量来分面：会生成一个网格，其中行表示不同的变速箱类型，列表示不同的气缸数。每个单元格中的子图将显示对应组合的 mpg（每加仑英里数）的密度图。

Population vs. Sample 总体与样本

population 总体：所有样本

Sample 样本：通过抽样方法从总体挑选的子集

抽样Sampling方法的类型

根据研究目标使用不同的抽样技术。常见方法包括：

• *简单随机抽样Simple Random Sampling（SRS）：总体中的每个元素都有相同的被选中机会。
• *分层抽样Stratified Sampling：将总体划分为子组（层），并从每个子组中按比例抽取样本。
• *整群抽样Cluster Sampling：将总体划分为群组，并随机选择整个群组。
• *系统抽样Systematic Sampling：在随机起点后每隔 kk 个元素选择一个。
• *便利抽样Convenience Sampling：一种非随机技术，基于易于访问选择元素。

# Create a population of 100 numbers
population <- 1:100
# Draw a random sample of size 10 without replacement
sample_data <- sample(population, size = 10, replace = FALSE)
# Print the sampled data
print(sample_data)

Expectation and Linearity 期望E 和 线性性

就是理论平均值。注意其计算是可能的事件值与其发生概率的乘积之和，而不仅仅是概率之和。

对于具有概率质量函数（PMF）( P(X = x_i) ) 的离散随机变量 ( X )，期望（或期望值）由下式给出：

$$
E[X] = \sum_i x_i P(X = x_i)
$$

对于具有概率密度函数（PDF）( f(x) ) 的连续随机变量，期望定义为：

$$
E[X] = \int_{-\infty}^{\infty} x f(x) \, dx
$$

期望具有线性性，它指出对于任何两个随机变量 X 和 Y ，以及任何常数 a 和 b ：$$
E[aX + bY] = aE[X] + bE[Y]
$$无论 ( X ) 和 ( Y ) 是否独立，此性质都成立。

//计算离散随机变量期望值
# Define a discrete random variable X with values and probabilities
values <- c(1, 2, 3, 4, 5)
probabilities <- c(0.1, 0.2, 0.3, 0.2, 0.2)

# Compute the expected value E[X]
expected_value <- sum(values * probabilities)

# Print result
print(expected_value)

//对于连续随机变量，使用蒙特卡洛模拟
# 模拟 X 的期望，其中 X ~ Uniform(0,1)
set.seed(42) # 设置种子以确保可重复性
samples <- runif(10000) # 从 U(0,1) 生成 10,000 个随机值

# 计算样本均值作为期望的近似值
expected_value_simulated <- mean(samples)

# 打印结果
print(expected_value_simulated)

蒙特卡洛模拟 ：通过从随机采样来估计随机变量X的期望（目标量），根据大数定律，当样本数量 N 足够大时，样本均值会趋近于期望值：

$$
E[X] \approx \frac{1}{N} \sum_{i=1}^{N} X_i
$$$$
\lim_{n \to \infty} \frac{1}{n} \sum_{i=1}^{n} X_i = \mu \quad (\text{几乎必然})
$$

大数定律为蒙特卡洛模拟提供了理论基础，确保大样本量能够产生可靠的期望值近似。

Variance 方差

衡量离散度的基本指标，度量随机变量和其数学期望（即均值）之间的偏离程度。计算公式为随机变量 X 与它的期望值之差的平方的期望

$$\text{Var}(X) = E\left[(X – E[X])^2\right]$$For a discrete random variable with probability mass function (PMF)$$\text{Var}(X) = \sum_{i}(x_i – E[X])^2P(X = x_i) $$For a continuous random variable with probability density function (PDF)$$\text{Var}(X) = \int_{-\infty}^{\infty}(x – E[X])^2f(x)\,dx$$

一个等价但在计算上更方便的方差公式，计算均值和平方值比计算与均值的偏差更容易

$$\text{Var}(X) = E[X^{2}] – (E[X])^{2}$$

从定义出发推导常用计算公式
展开平方项：
\[
(X – \mathbb{E}(X))^2 = X^2 – 2X \cdot \mathbb{E}(X) + [\mathbb{E}(X)]^2
\]取期望\[
\mathbb{E}\left[(X – \mathbb{E}(X))^2\right] = \mathbb{E}(X^2) – 2\mathbb{E}(X) \cdot \mathbb{E}(X) + [\mathbb{E}(X)]^2
\]
这里用到了期望的线性性质：
\[
\circ \quad \mathbb{E}(aX + b) = a\mathbb{E}(X) + b
\]
\(\mathbb{E}(X)\) 是一个常数（因为它是 \(X\) 的期望值，已固定），因此可以提到期望外面：
\[
\mathbb{E}\left[2X \cdot \mathbb{E}(X)\right] = 2\mathbb{E}(X) \cdot \mathbb{E}(X).
\]\[
\mathbb{E}(X^2) – 2[\mathbb{E}(X)]^2 + [\mathbb{E}(X)]^2 = \mathbb{E}(X^2) – [\mathbb{E}(X)]^2
\]

与期望不同，方差并不完全遵循线性规则。然而，对于两个随机变量 X 和 Y，它们的线性组合的方差满足：$$\text{Var}(aX + bY + c) = a^2\text{Var}(X) + b^2\text{Var}(Y) + 2ab \text{Cov}(X,Y)$$其中 Cov(X,Y) 是 X 和 Y 的协方差

Covarience 协方差

$$\text{Cov}(X,Y) = E[(X – E[X])(Y – E[Y])]$$

衡量两个随机变量之间线性关系的统计量，即两个变量的变化趋势是否一致

• 如果协方差为正，两个随机变量都大于/小于自身的期望值。表示两个变量倾向于同时增加或减少，即它们之间存在正相关关系。
• 如果协方差为负，表示一个变量增加时另一个变量倾向于减少，即它们之间存在负相关关系。
• 如果协方差为零，表示两个变量之间没有线性关系。这将方差公式简化为：\({Cov}(X,Y) = E[(X – E[X])(Y – E[Y])]\)

假设有两个独立的随机变量 X 和 Y，其方差分别为 Var(X)=4 和 Var(Y)=9。我们想算 Z=2X+3Y 的方差。

由于 X 和 Y 是独立的，协方差为零，因此：Var(Z)=Var(2X+3Y)=22⋅Var(X)+32⋅Var(Y)=4⋅4+9⋅9=16+81=97

Standard Deviation 标准差

虽然方差很好的描述数据与均值的偏离程度，但方差与我们要处理的数据的量纲是不一致导致处理结果是不符合我们的直观思维的

举个例子：一个班级里有60个学生，平均成绩是70分，标准差是9，方差是81，假设成绩服从正态分布，那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分，通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为68%，即约等于下图中的34.2%*2

标准差，记作 \((\sigma_X)\)，是方差的平方根 $$\sigma_X = \sqrt{\text{Var}(X)}$$

Variance can be computed in R using the var() function

# Generate a sample dataset
data <- c(5, 7, 10, 15, 20)

# Compute variance
variance_value <- var(data)

# Compute standard deviation
std_dev <- sd(data)

# Print results
print(variance_value)
print(std_dev)

期望Expected Value，方差Variance，标准差standard deviation例题

我们有一个离散随机变量 \( X \)，其概率分布如下：\[
\mathbb{P}(X = x) =
\begin{cases}
0.37 & \text{当 } x = 0 \\
0.39 & \text{当 } x = 1 \\
0.19 & \text{当 } x = 2 \\
0.04 & \text{当 } x = 3 \\
0.01 & \text{当 } x = 4
\end{cases}
\]需要计算 \( X \) 的期望值（Expected Value）、方差（Variance）和标准差（Standard Deviation）。
期望值 \( E(X) \) 的计算公式为：
\[E(X) = \sum x \cdot P(X = x)\]\[\begin{aligned}
E(X) &= 0 \times 0.37 + 1 \times 0.39 + 2 \times 0.19 + 3 \times 0.04 + 4 \times 0.01 \\
&= 0 + 0.39 + 0.38 + 0.12 + 0.04 \\
&= 0.93\end{aligned}
\]方差的计算公式为：\[
\begin{aligned}
\text{Var}(X) &= E(X^2) – [E(X)]^2 \\
&= 1.67 – (0.93)^2 \\
&= 1.67 – 0.8649 \\
&= 0.8051
\end{aligned}
\]标准差是方差的平方根：\[
\sigma = \sqrt{\text{Var}(X)} = \sqrt{0.8051} \approx 0.8973
\]

样本方差

对于样本数据集，样本方差使用以下公式计算： \[ S^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i – \bar{X})^2 \]

对于具有 \( n \) 个观测值 \( x_1, x_2, \ldots, x_n \) 的样本数据集，样本均值计算为： \[ \bar{X} = \frac{1}{n} \sum_{i=1}^n x_i \]

\( S^2 \) 是样本方差，使用 \((n-1)\) 作为分母（贝塞尔校正）以考虑估计总体方差时的偏差

# 总体期望和方差
x <- c(1, 2, 3, 4, 5)
p <- c(0.1, 0.2, 0.3, 0.2, 0.2) # 概率

EX <- sum(x * p) # 总体期望
VarX <- sum((x^2) * p) - EX^2 # 总体方差

# 样本均值和样本方差
sample_mean <- mean(x) # 样本均值
sample_variance <- var(x) # 样本方差（使用n-1）
# 手动计算样本方差

# 计算与均值的平方偏差
squared_deviations <- (x - sample_mean)^2

# 平方偏差的总和
sum_squared_deviations <- sum(squared_deviations)

# 计算样本方差（使用n-1作为分母）
n <- length(x) # 样本大小
sample_variance_by_hand <- sum_squared_deviations / (n - 1)

Binomial Distribution 二项分布

条件：

1. 某个事件发生的次数（或者实验次数）有限且固定
2. 事件的结果有且只有两种（成功或失败）
3. 事件的结果的概率相等。比如每次抛硬币相同面朝上的概率是一样的

公式：假设试验成功的概率为 \( p \)，所以失败的概率为 \( 1 – p \)，设为 \( q \)。现在进行这个试验，假设这个试验进行了 \( n \) 次，有 \( r \) 次获得了成功。用二项分布的概率质量函数表示为： \[ P(X = r) = C_n^r \ p^r \ q^{n-r} \]

计算 r次成功的概率，必须同时考虑 n−r 次失败的概率，因为试验的所有结果都需要被考虑。乘以组合数因为成功和失败的顺序可以不同。例如，在 n=3次试验中，恰好 k=2次成功可能是失败、成功、成功；成功、成功、失败；成功、失败、成功

符号 X∼B(n,p)表示随机变量 X服从参数为 n 和 p 的二项分布。n表示试验的次数。p表示每次试验成功的概率。

例：沿着某条赛道行驶的山地自行车骑手爆胎的概率为 0.05。求在 17 名骑手中：

(a) 恰好有一人爆胎

(b) 最多三人爆胎

P(X=0)+P(X=1)+P(X=2)+P(X=3)\[
\mathbb{P}(X \leq 3) \approx 0.4181 + 0.3741 + 0.1575 + 0.0415 \approx 0.9912
\]

(c) 两人或更多人爆胎

需要计算 P(X≥2)，即 1−P(X<2)=1−P(X=0)−P(X=1)\[
\mathbb{P}(X \geq 2) = 1 – 0.4181 – 0.3741 \approx 0.2078
\]

解. 设 X为爆胎的骑手数量，则 X∼B(17,0.05)，表示试验次数17次，每次爆胎的概率为0.05

\[
\mathbb{P}(X = 0) = C(17, 0) \cdot (0.05)^0 \cdot (0.95)^{17} = 1 \cdot 1 \cdot (0.95)^{17} \approx 0.4181
\]\[
\mathbb{P}(X=1) = C(17,1) \cdot (0.05)^1 \cdot (0.95)^{16}
\]\[
\mathbb{P}(X = 2) = C(17, 2) \cdot (0.05)^2 \cdot (0.95)^{15} = 136 \cdot 0.0025 \cdot (0.95)^{15} \approx 136 \cdot 0.0025 \cdot 0.4633 \approx 0.1575
\]\[
\mathbb{P}(X = 3) = C(17, 3) \cdot (0.05)^3 \cdot (0.95)^{14} = 680 \cdot 0.000125 \cdot (0.95)^{14} \approx 680 \cdot 0.000125 \cdot 0.4877 \approx 0.0415
\]

# Binomial probability distribution
n <- 10 # Number of trials
p <- 0.5 # Probability of success
x <- 0:n # Possible values of X
prob <- dbinom(x, size=n, prob=p)
 
# Plotting
barplot(prob, names.arg=x, col="blue",main="Binomial Distribution (n=10, p=0.5)",
xlab="Number of Successes", ylab="Probability")

Geometric Distribution 几何分布

与二项分布的“n次实验k次成功的概率”不同，几何分布关心的是，试验k次才得到第一次成功的机率。用几何分布的概率质量函数表示为：
\[
P\left( X = k \right) = \left( 1 – p \right)^{k – 1} p, \quad k = 1, 2, \ldots
\]

记作Y∼Geometric(p)，P表示成功的概率，注意与二项分布相同，每次事件发生(成功)的概率是相同的

期望推导：

几何分布的期望定义为：
\[
E(Y) = \sum_{m=1}^{\infty} m \cdot P(Y=m)
\]根据几何分布的概率质量函数 \( P(Y=m) = p(1-p)^{m-1} \)，代入上式：
\[
E(Y) = \sum_{m=1}^{\infty} m \cdot p(1-p)^{m-1}
\]将 \( p \) 提出求和符号：\[
E(Y) = p \sum_{m=1}^{\infty} m(1-p)^{m-1}
\]我们知道，对于 \( |x| < 1 \)，有：\[
\sum_{m=1}^{\infty} mx^{m-1} = \frac{1}{(1-x)^2}
\]令 \( x = 1 – p \)，则：\[
\sum_{m=1}^{\infty} m(1-p)^{m-1} = \frac{1}{(1-(1-p))^2} = \frac{1}{p^2}
\]因此：\[
E(Y) = p \cdot \frac{1}{p^2} = \frac{1}{p}
\]

Poisson Distribution 泊松分布

如果二项分布有非常大的 n 值/非常小的p值时，或者题目给出了平均发生率/(lambda/)时，可以简化计算，在满足np=λ（常数）时，我们可以在以下条件下简化二项概率公式：

np=λ 的常数性保证了模型在近似时的稳定性。例如，在单位时间内电话呼叫次数、放射性衰变事件等场景中，尽管事件概率 pp 极低，但大量独立试验下事件的平均发生率 λ 是固定的。

$$
\begin{align*}
\mathbb{P}(X=k) \approx e^{-\lambda} \tfrac{\lambda^k}{k!}.
\end{align*}
$$定义了参数为 λ 的泊松分布 Z。我们将假设它给出了X∼B(n,p)的有效近似，

• K也与二项分布一样表示某事件成功(发生)的次数。且 n≥100 和 p≤0.05 时成立，记为Z∼Poisson(λ)
• λ = np，根据题目给出的条件计算(n表示试验的次数。p表示每次试验成功的概率)。

E(Z)=Var(Z)=λ

例：批量生产的针以每盒 10001000 支包装。据信，平均每 20002000 支针中有 11 支不合格。求一盒中有 22 支或更多不合格针的概率

由于 n较大且 p较小，可以使用泊松分布来近似二项分布。泊松分布的参数 λ为：λ=n⋅p=1000⋅0.0005=0.5

我们需要计算 \(\mathbb{P}(X \geq 2)\), 即:
\[
\mathbb{P}(X \geq 2) = 1 – \mathbb{P}(X = 0) – \mathbb{P}(X = 1)
\]
计算 \(\mathbb{P}(X = 0)\) 和 \(\mathbb{P}(X = 1)\):
\[
\mathbb{P}(X = 0) = e^{-0.5} \frac{0.5^0}{0!} = e^{-0.5} \approx 0.6065
\]
\[
\mathbb{P}(X = 1) = e^{-0.5} \frac{0.5^1}{1!} = 0.5 \cdot e^{-0.5} \approx 0.3033
\]
因此:
\[
\mathbb{P}(X \geq 2) = 1 – 0.6065 – 0.3033 = 0.0902
\]

例2：

Continuous Random Variables

通过类比离散情况，我们的概率分布将是一个函数\(f_X : \mathbb{R} \to [0; 1]\)

在概率论中，概率质量函数（probability mass function，简写为 pmf）是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数不同之处在于：概率质量函数是对离散随机变量定义的，本身代表该值的概率；概率密度函数是对连续随机变量定义的，本身不是概率，讨论连续型随机变量取某个具体值的概率没有意义，只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率

用于描述与随机变量相关的连续概率分布的函数称为\textbf{概率密度函数}。根据概率密度函数的定义，对于实数值 \( a < b \)，\( X \) 在 \( a \) 和 \( b \) 之间取值的概率为：

各种概率分布对应了不同的f(x)，上面的二项、几何、泊松都是离散变量的概率分布分别带入不同的公式。还有常见的连续变量的概率分布，有均匀分布、指数分布、正态分布。

Uniform Distribution 均匀分布

均匀分布既可以是离散型的，也可以是连续型的

若随机变量 X 在连续区间 [a,b]上取值，且任意子区间的概率密度相同，则服从连续均匀分布。

例题：

Exponential Distribution 指数分布

例题：

例2：

Normal Distribution正态分布 / Gaussian Distribution 高斯分布

二项分布的条件和几何分布相同，泊松分布是对二项分布在一定条件下的近似，但这些都是离散变量的分布，接下来是连续变量的分布，正态分布描述了由均值 \(\mu\) 和标准差 \(\sigma\) 表征的连续概率分布,通常记作 \(X \sim N(\mu, \sigma^2)\)。概率密度函数（PDF）为：

– \(\mu\)（均值）：分布的中心位置。
– \(\sigma\)（标准差）：衡量分布的扩散程度。
– \(\sigma^2\)（方差）：量化值的离散程度。
– 归一化因子 \(\frac{1}{\sigma\sqrt{2\pi}}\)：确保总概率积分为1。
– 指数项 \(e^{-\frac{(x – \mu)^2}{2\sigma^2}}\)：控制钟形形状，随着 \(x\) 远离 \(\mu\)，概率减小。

正态分布的概率密度函数显示为典型的钟形曲线，这一形状类似于寺庙中的大钟，因此也常被称为钟形曲线。作为一种连续分布，正态分布拥有完备的概率密度函数(上)、累积分布函数(下)、矩生成函数(拉普拉斯变换)和特征函数等表达形式，并且具备明确的期望（即均值）、方差、偏度和峰度等数值特征

累积分布函数（CDF） – F

表示随机变量X取值小于或等于给定值x的概率，离散型随机变量的累积分布函数 \( F(x) \) 定义为：\[
F(x) = \sum_{x_i \leq x} f(x_i).
\]对于连续型随机变量 \( X \)，其累积分布函数 \( F_X(x) \) 定义为：
\[
F_X(x) = \mathbb{P}(X \leq x) = \int_{-\infty}^{x} f_X(t) \, dt,
\]其中 \( f_X(x) \) 是概率密度函数（PDF）。根据微积分基本定理，对 \( F_X(x) \) 求导即可恢复 PDF：\[
f_X(x) = \frac{d}{dx} F_X(x).
\]对累积分布函数（CDF）求导可以得到概率密度函数（PDF）

为什么不需要乘以自变量：CDF 的目的是计算 X落在某个区间内的概率（如 P(X≤x)。在计算某些期望值或矩时，会用到 x 与概率的乘积

# CDF using empirical distribution function
library(ggplot2)
 
ggplot(data.frame(x=mtcars$mpg), aes(x)) +
stat_ecdf(geom="step", color="blue") +
labs(title="Cumulative Distribution Function of MPG",x="Miles Per Gallon", y="Cumulative Probability")

ECDF是一种直接从数据中得出的累积分布函数，适用于非参数统计，能够在不假设数据分布的情况下提供经验概率估计。这使得它在数据分析和统计推断中非常实用。

例1. 某公司为顾客生产了七台大型机器，其中三台不符合顾客的规格要求。质检员随机抽取两台机器进行检查。设离散型随机变量 X表示被检查的机器中符合顾客规格的数量。

随机变量变换

无论是单调递增还是单调递减，公式的形式是一样的，因为导数取绝对值已经包含了方向的信息。

其他例题：