Partial derivatives 偏导数 – Skyshin34的博客

本文最后更新于39 天前，其中的信息可能已经过时，如有错误请留言

定义

$z = f(x, y)$，f在点$(x_0, y_0)$处关于x的偏导数是当$y = y_0$保持不变，x变化时所得函数在$x_0$处的导数。记为$f_x(x_0, y_0)$，其表达式为： $$f_x(x_0, y_0)=\left.\frac{d}{dx}[f(x, y_0)]\right|_{x = x_0}=\lim_{\Delta x \to 0}\frac{f(x_0 + \Delta x, y_0)-f(x_0, y_0)}{\Delta x}$$

类似地，f在点$(x_0, y_0)$处关于y的偏导数（也称为z在点$(x_0, y_0)$处关于y的偏导数）是当$x = x_0$保持不变，y变化时所得函数在$y_0$处的导数。记为$f_y(x_0, y_0)$，其表达式为： $$f_y(x_0, y_0)=\left.\frac{d}{dy}[f(x_0, y)]\right|_{y = y_0}=\lim_{\Delta y \to 0}\frac{f(x_0, y_0 + \Delta y)-f(x_0, y_0)}{\Delta y}$$

例 1：$f(x, y)=2x^3y^2 + 2y + 4x$，求$f_x(1, 3)$和$f_y(1, 3)$
$f_x(x, 3)=\frac{d}{dx}[f(x, 3)]=\frac{d}{dx}[18x^3 + 4x + 6]=54x^2 + 4$
所以$f_x(1, 3)=54 + 4 = 58$。又因为
$f_y(1, y)=\frac{d}{dy}[f(1, y)]=\frac{d}{dy}[2y^2 + 2y + 4]=4y + 2$
所以$f_y(1, 3)=4×3 + 2 = 14$

然而，通常我们希望省略下标，将偏导数看作变量x和y的函数。这些函数为：
$f_x(x, y)=\lim_{\Delta x \to 0}\frac{f(x + \Delta x, y)-f(x, y)}{\Delta x}$
$f_y(x, y)=\lim_{\Delta y \to 0}\frac{f(x, y + \Delta y)-f(x, y)}{\Delta y}$

同样对于$f(x, y)=2x^3y^2 + 2y + 4x$，求$f_x(x, y)$和$f_y(x, y)$，并用这些偏导数计算$f_x(1, 3)$和$f_y(1, 3)$。
解：对谁求偏导谁就变，其他视为常数

保持y不变，对x求导可得：
$f_x(x, y)=\frac{d}{dx}[2x^3y^2 + 2y + 4x]=6x^2y^2 + 4$
保持x不变，对y求导可得：
$f_y(x, y)=\frac{d}{dy}[2x^3y^2 + 2y + 4x]=4x^3y + 2$
因此，
$f_x(1, 3)=6×1^2×3^2 + 4 = 58$
$f_y(1, 3)=4×1^3×3 + 2 = 14$这与例 1 的结果一致。

若$z = f(x, y)$，那么偏导数$f_x$和$f_y$也可以用符号$\frac{\partial f}{\partial x}$、$\frac{\partial z}{\partial x}$以及$\frac{\partial f}{\partial y}$、$\frac{\partial z}{\partial y}$来表示。

对于$z = f(x, y)$在点$(x_0, y_0)$处的偏导数，一些常见的符号表示有： $\left.\frac{\partial f}{\partial x}\right|_{x = x_0, y = y_0},\left.\frac{\partial z}{\partial x}\right|_{(x_0, y_0)},\left.\frac{\partial f}{\partial x}\right|_{(x_0, y_0)},\frac{\partial f}{\partial x}(x_0, y_0),\frac{\partial z}{\partial x}(x_0, y_0)$

例3 复合函数求偏导：若$z = x^4\sin(xy^3)$，求$\frac{\partial z}{\partial x}$和$\frac{\partial z}{\partial y}$。

$\begin{align*} \frac{\partial z}{\partial x}&=\frac{\partial}{\partial x}[x^4\sin(xy^3)]\\ &=x^4\frac{\partial}{\partial x}[\sin(xy^3)]+\sin(xy^3)\cdot\frac{\partial}{\partial x}(x^4)\\ &=x^4\cos(xy^3)\cdot y^3+\sin(xy^3)\cdot4x^3\\ &=x^4y^3\cos(xy^3)+4x^3\sin(xy^3) \end{align*}$ $\begin{align*} \frac{\partial z}{\partial y}&=\frac{\partial}{\partial y}[x^4\sin(xy^3)]\\ &=x^4\frac{\partial}{\partial y}[\sin(xy^3)]+\sin(xy^3)\cdot\frac{\partial}{\partial y}(x^4)\\ &=x^4\cos(xy^3)\cdot3xy^2+\sin(xy^3)\cdot0\\ &=3x^5y^2\cos(xy^3) \end{align*}$

复合函数的偏导数为下面隐函数求偏导的基础

例4 复合函数求偏导：偏导数定义法，

偏导数的几何含义

设$f(x, y)=x^2y + 5y^3$。
（a）求曲面$z = f(x, y)$在点$(1, -2)$处x方向的斜率。
（b）求曲面$z = f(x, y)$在点$(1, -2)$处y方向的斜率。
解（a）：保持y不变，对x求导可得$f_x(x, y)=2xy$。因此，x方向的斜率为$f_x(1, -2)= – 4$，即x每增加一个单位，z以4个单位的速率减少。
解（b）：保持x不变，对y求导可得$f_y(x, y)=x^2 + 15y^2$。因此，y方向的斜率为$f_y(1, -2)=61$，即y每增加一个单位，z以6个单位的速率增加。

Implicit Partial Differentiation 隐函数求偏导数

隐函数和函数的区别在于是否将因变量显式写成自变量的函数形式。例如 $ y = f(x) $；而隐函数中变量关系隐藏在一个方程中，如 $ x^2 + y^2 = 1 $。在求导时，隐函数比显函数更复杂，往往涉及链式法则与复合函数的导数。虽然显函数中也可能出现复合函数

例1求球面$x^{2}+y^{2}+z^{2}=1$在点$(\frac{2}{3},\frac{1}{3},\frac{2}{3})$和$(\frac{2}{3},\frac{1}{3},-\frac{2}{3})$处y方向的斜率 Slope

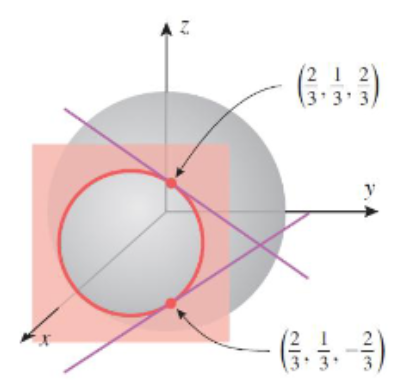
解：

可以分别对z的每个表达式关于y求导，然后在$x = \frac{2}{3}$和$y = \frac{1}{3}$处计算导数来得到斜率。

然而，对给定方程$x^{2}+y^{2}+z^{2}=1$关于y隐式求导会更高效，因为这样一次求导就能得到两个斜率。进行隐式求导时，把z看作x和y的函数(保留完整)，对等式两边关于y求导，同时把x看作常量：
$\frac{\partial}{\partial y}(x^{2}+y^{2}+z^{2})=\frac{\partial}{\partial y}(1)$
$0 + 2y + 2z\frac{\partial z}{\partial y}=0$
$\frac{\partial z}{\partial y}=-\frac{y}{z}$
将点$(\frac{2}{3},\frac{1}{3},\frac{2}{3})$和$(\frac{2}{3},\frac{1}{3},-\frac{2}{3})$的y坐标和z坐标代入这个表达式，得到点$(\frac{2}{3},\frac{1}{3},\frac{2}{3})$处的斜率为$-\frac{1}{2}$，点$(\frac{2}{3},\frac{1}{3},-\frac{2}{3})$处的斜率为$\frac{1}{2}$

例2：假设$D = \sqrt{x^{2}+y^{2}}$是一个矩形对角线的长度，该矩形的边长x和y是可以变化的。求当y保持不变x变化时D关于x的变化率公式，并使用这个公式求在$x = 3$，$y = 4$这一点D关于x的变化率。
解：对等式$D^{2}=x^{2}+y^{2}$两边关于x求导可得(对x求偏导，y为常数，z为复合函数—一次函数）
$2D\frac{\partial D}{\partial x}=2x$，因此$D\frac{\partial D}{\partial x}=x$
当$x = 3$，$y = 4$时，$D = 5$，由此可得：
$\left.5\frac{\partial D}{\partial x}\right|_{x = 3,y = 4}=3$，即$\left.\frac{\partial D}{\partial x}\right|_{x = 3,y = 4}=\frac{3}{5}$
所以，在点$(3,4)$处，x每增加一个单位，D以$\frac{3}{5}$个单位的速率增加。

快速计算公式：

偏导数与连续性

与单变量函数的情况不同，多变量函数偏导数的存在并不能保证函数是连续的。下面的例子说明了这一事实

例：设
$f(x,y)=\begin{cases}-\frac{xy}{x^{2}+y^{2}},(x,y)\neq(0,0)\\0,(x,y)=(0,0)\end{cases}$
（a）证明$f_{x}(x,y)$和$f_{y}(x,y)$在所有点$(x,y)$处都存在。
（b）解释为什么f在点$(0,0)$处不连续。
解（a）：
$f_{x}(x,y)=-\frac{(x^{2}+y^{2})y – xy(2x)}{(x^{2}+y^{2})^{2}}=\frac{x^{2}y – y^{3}}{(x^{2}+y^{2})^{2}}$
$f_{y}(x,y)=-\frac{(x^{2}+y^{2})x – xy(2y)}{(x^{2}+y^{2})^{2}}=\frac{xy^{2}-x^{3}}{(x^{2}+y^{2})^{2}}$
f在点$(0,0)$处是否有偏导数并不明显，如果有，这些导数的值是多少也不清楚。为了回答这个问题，我们需要使用偏导数的定义：
$f_{x}(0,0)=\lim_{\Delta x \to 0}\frac{f(\Delta x,0)-f(0,0)}{\Delta x}=\lim_{\Delta x \to 0}\frac{0 – 0}{\Delta x}=0$
$f_{y}(0,0)=\lim_{\Delta y \to 0}\frac{f(0,\Delta y)-f(0,0)}{\Delta y}=\lim_{\Delta y \to 0}\frac{0 – 0}{\Delta y}=0$
这表明f在点$(0,0)$处有偏导数，并且这两个偏导数在该点的值都为0。
解（b）：
$\lim_{(x,y)\to(0,0)}-\frac{xy}{x^{2}+y^{2}}$不存在。因此，f在点$(0,0)$处不连续。

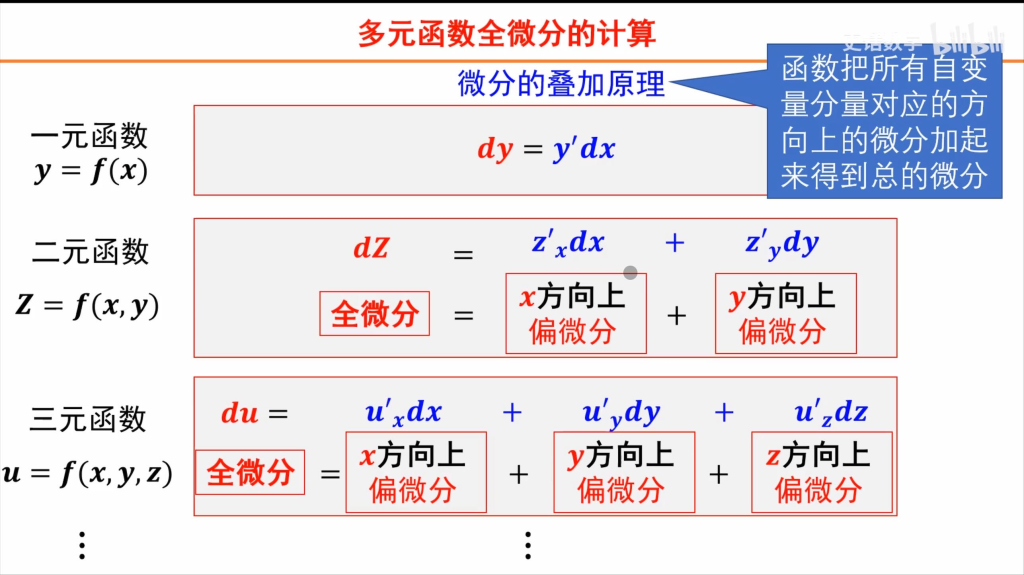
多元函数的偏导数 – 全微分

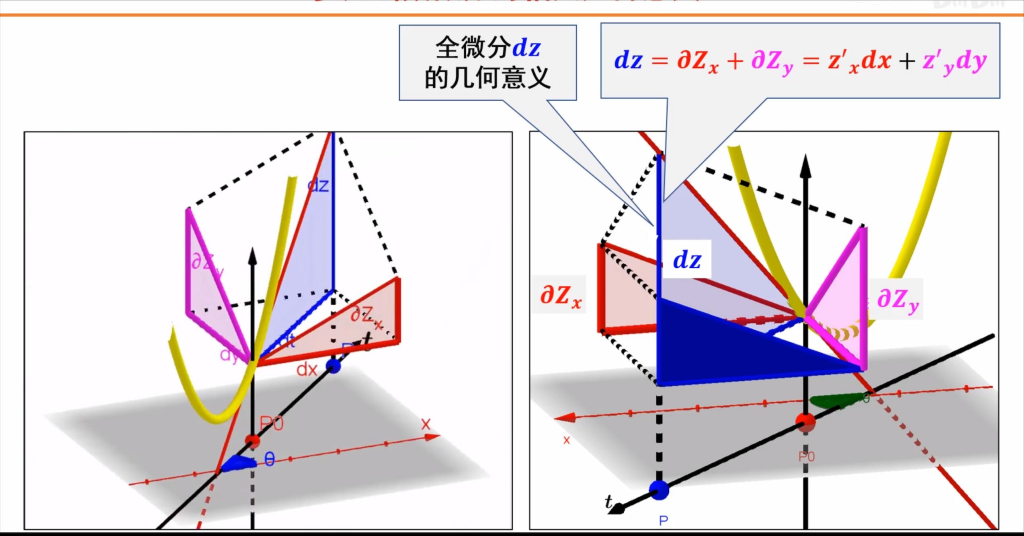
如果$f(x,y,z)=x^{3}y^{2}z^{4}+2xy + z$，那么
$f_{x}(x,y,z)=3x^{2}y^{2}z^{4}+2y$
$f_{y}(x,y,z)=2x^{3}yz^{4}+2x$
$f_{z}(x,y,z)=4x^{3}y^{2}z^{3}+1$
$f_{z}(-1,1,2)=4\times(-1)^{3}\times(1)^{2}\times(2)^{3}+1=-31$

高阶偏导数

多元函数的全微分 total differential

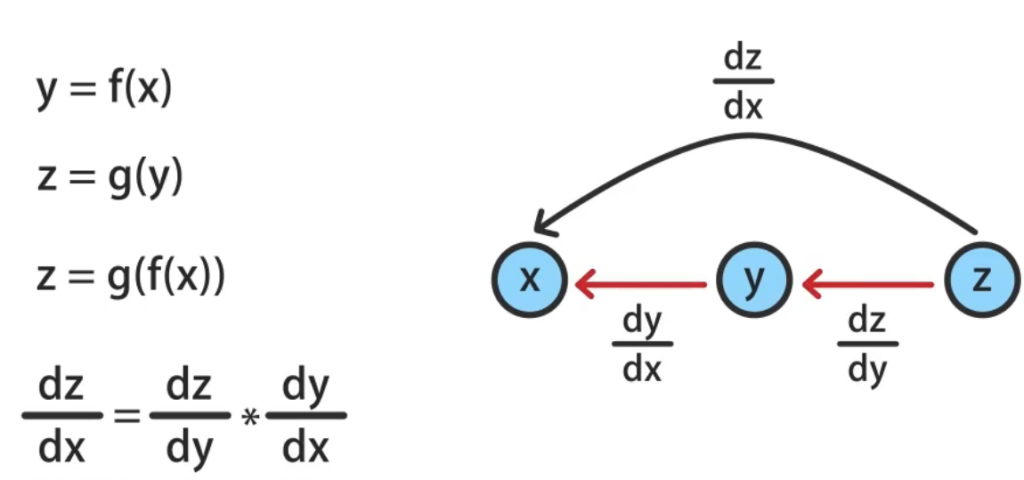
复合函数求偏导 – 链式法则

x+y 和 u = x+y

把 x + y 抽象成“中间变量，用于分层分析变量依赖；而 x + y 是一个具体表达式，无法表示结构关系。

设: $u = x + y$$H = \ln(u)$

链式法则$\frac{dH}{dx} = \frac{dH}{du} \cdot \frac{du}{dx} = \frac{1}{u} \cdot 1 = \frac{1}{x + y}$

直接代入展开$H = \ln(x + y) \Rightarrow \frac{dH}{dx} = \frac{1}{x + y}$

可以发现其实求偏导数来说两者没有区别

链式法则

连线相乘，分线相加

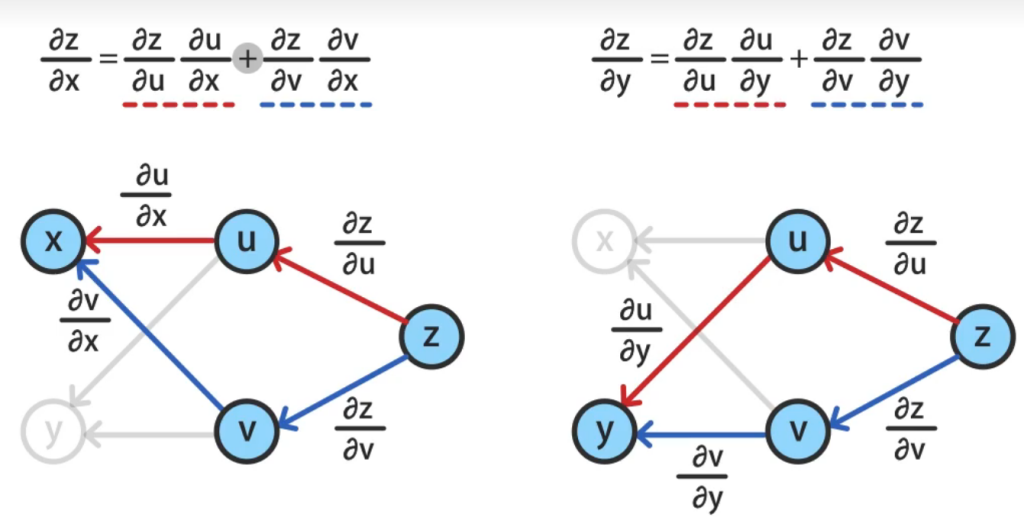
例1：链式法则中，x同时直接和间接影响 H

$u = x^2 + y$； $v = \sin(y)$； $w = \ln(x)$； $H(u, v, w, x, y) = u + v \cdot w + x^3 y$

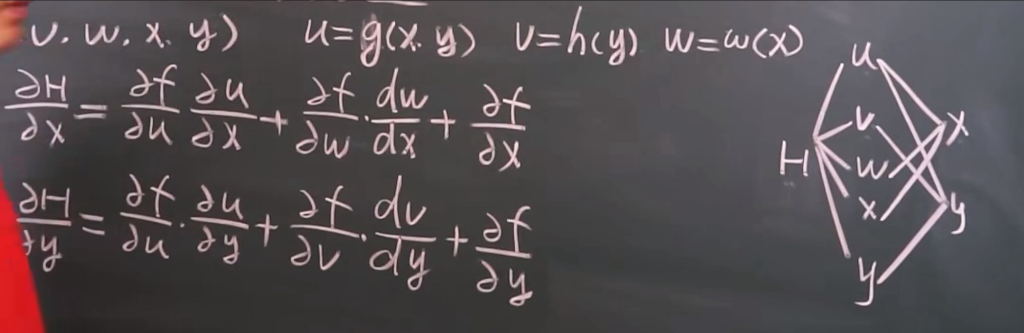
\[ \frac{\partial H}{\partial x} = \frac{\partial H}{\partial u} \cdot \frac{\partial u}{\partial x} + \frac{\partial H}{\partial w} \cdot \frac{\partial w}{\partial x} + \frac{\partial H}{\partial x} \cdot \frac{\partial x}{\partial x} \]

\[ \frac{\partial H}{\partial x} = 1 \cdot 2x + v \cdot \frac{1}{x} + 3x^2 y = 2x + \frac{\sin(y)}{x} + 3x^2 y \]

例2：多元复合函数求导

如果有

高阶偏导数 Higher-Order Partial Derivatives

注意，混合二阶偏导数的两种表示法在顺序上有相反的约定
$\frac{\partial^{2} f}{\partial y \partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)$
从右到左。先对括号内的部分求导。
$f_{x y}=\left(f_{x}\right)_{y}$
从左到右。先对括号内的部分求导。

求$f(x, y)=x^{2} y^{3}+x^{4} y$的二阶偏导数。
解：我们有
$\frac{\partial f}{\partial x}=2 x y^{3}+4 x^{3} y$和$\frac{\partial f}{\partial y}=3 x^{2} y^{2}+x^{4}$
因此
$\frac{\partial^{2} f}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial}{\partial x}\left(2 x y^{3}+4 x^{3} y\right)=2 y^{3}+12 x^{2} y$
$\frac{\partial^{2} f}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial}{\partial y}\left(3 x^{2} y^{2}+x^{4}\right)=6 x^{2} y$
$\frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial}{\partial x}\left(3 x^{2} y^{2}+x^{4}\right)=6 x y^{2}+4 x^{3}$
$\frac{\partial^{2} f}{\partial y \partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial}{\partial y}\left(2 x y^{3}+4 x^{3} y\right)=6 x y^{2}+4 x^{3} \triangleleft$
三阶、四阶和更高阶的偏导数可以通过逐次求导得到。一些可能的情况是
$\frac{\partial^{3} f}{\partial x^{3}}=\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial x^{2}}\right)=f_{x x x}$ $\frac{\partial^{4} f}{\partial y^{4}}=\frac{\partial}{\partial y}\left(\frac{\partial^{3} f}{\partial y^{3}}\right)=f_{y y y y}$
$\frac{\partial^{3} f}{\partial y^{2} \partial x}=\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial y \partial x}\right)=f_{x y y}$ $\frac{\partial^{4} f}{\partial y^{2} \partial x^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial^{3} f}{\partial y \partial x^{2}}\right)=f_{x x y y}$

函数在某点得连续保证了函数的局部变化率与路径无关，可以想象如果一个函数在某点连续，即函数可以在该点找到一个切平面，那无论是什么顺序求该点的切线，最后组合出来的都是同一个切平面，所以

多元函数的可微性 Differentiability

可微要指定在某个X或某个点处，不能说整个函数是可微的

所有偏导数存在只保证函数在每个坐标方向都有切线，但并不能保证这些切线能组合成一个真正的/切线切平面，求极限保证沿着所有偏导数方向逐渐逼近某个点时，真实变化量和线性估计量的误差项远小于步长长度本身。

回想一下，一元函数 f 在$x_{0}$处可微，是指它在$x_{0}$处有导数，即极限
$f’\left(x_{0}\right)=\lim _{\Delta x \to 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} (1)$存在

$y=f(x)$的图像在点$(x_{0}, f(x_{0}))$处有非垂直的切线；
f 在$x_{0}$附近可以用线性函数很好地近似；
f 在$x_{0}$处连续。

将可微性的概念推广到二元或三元函数，先直观理解多元函数可微的含义：若二元函数$f(x, y)$在点$(x_{0}, y_{0})$处可微，曲面$z=f(x, y)$在点$(x_{0}, y_{0}, f(x_{0}, y_{0}))$处有非垂直的切平面；那么就能看懂定义了

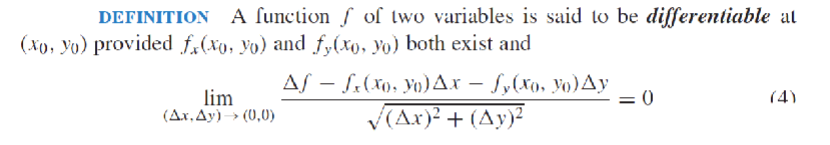
偏导数等于什么时可以看出偏导数不存在：

1.极限不存在或震荡你使用偏导定义: $f_x(x_0,y_0)=\lim_{h \to 0}\frac{f(x_0 + h,y_0)-f(x_0,y_0)}{h}$ 出现以下状况:

极限值依赖 $h \to 0^+$ 与 $h \to 0^-$，左右极限不一致；
极限值震荡，如含 $\sin(1/h)$、$\tan(1/h)$ 等；
极限发散（趋于正负无穷）；

2.表达式在该点未定义你化简后发现:

出现 $\sqrt{-1}$、$\ln(0)$、除 0 等非法项；
偏导表达式分母为 0；

证明见：连续,可微,可导,可偏微,全微分,可偏导 – Skyshin34的博客

多元函数的连续性

定义