词汇对照：

• Redidual 残差
• 在简单线性回归中，因变量也被称为响应变量，自变量也被称为预测变量
  • 因变量dependent variable – 响应变量response variable
  • 自变量 independent variable – 预测变量predictor variable(自变量的用途就是拿来预测因变量)
• Fit 拟合 Fitted value 拟合值
• Least Squares 最小二乘法
• coefficient of determination 决定系数 R2

含连续协变量的线性回归模型，残差是每个点的预测偏差 et = yt − Ŷt，Error 指的是把所有残差平方后加起来（残差平方和，SSE），这些被用进最小二乘法Least Squares

1.2 Correlation 相关性 – 皮尔逊相关系数 Pearson’s r

当一个变量的取值与另一个变量的取值相关联时，我们称这两个变量具有相关性

相关系数的取值范围在 – 1（完全负相关） 到 + 1 （完全正相关）之间。当r=0时，变量之间不存在相关性

1.3 简单线性回归模型 Simple linear regression model

简单线性回归是回归分析的一种特殊形式，在此模型中，仅有一个自变量影响因变量，且假设两个变量之间呈直线关系

我们将该模型表示为：

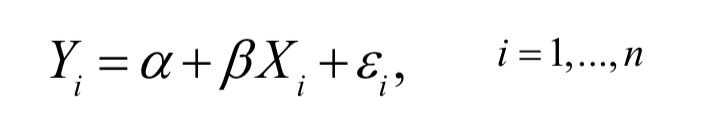
• Yi​是第i个个体的因变量
• Xi​是第i个个体的自变量
• 模型中的参数α被称为截距
• 模型中的参数β被称为回归系数
• εi​是第i个个体的残差

1.4 简单线性回归模型的拟合
Fitting the Simple linear regression model – 最小二乘法

我们可采用最小二乘法来估计线性回归模型中的α和β，为了找到最能代表数据总体趋势的回归直线，我们需要确定参数 $\alpha$ 和 $\beta$的取值，因此引入最小二乘法

残差平方和，即数据点到直线的垂直偏差（称为残差）的平方和，可表示为：

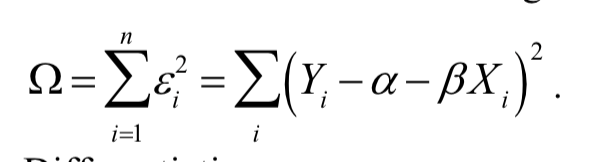
\((X_i,Y_i)\)：第i个数据点，\(X_i\)是自变量，\(Y_i\)是真实观测值。
\(\alpha,\beta\)：回归直线的参数\(\alpha\)：截距（intercept）
\(\beta\)：斜率（slope）
\(\hat{Y}_i = \alpha + \beta X_i\)：模型对第i个样本的预测值（回归直线在\(X_i\)处的高度）。
\(\varepsilon_i = Y_i – \hat{Y}_i = Y_i – (\alpha + \beta X_i)\)：第i个点的残差，也就是该点到回归直线的竖直方向差距（在一元线性回归里默认用竖直差）

为什么要平方再相加？

• 平方保证不出现正负抵消；
• 平方会对偏差大的点惩罚更重；
• 数学上也更容易求出最优的 $\alpha,\beta$α,β。

最小二乘法的核心就是：选择α,β，让 Ω（残差平方和）最小，从而得到最佳拟合直线

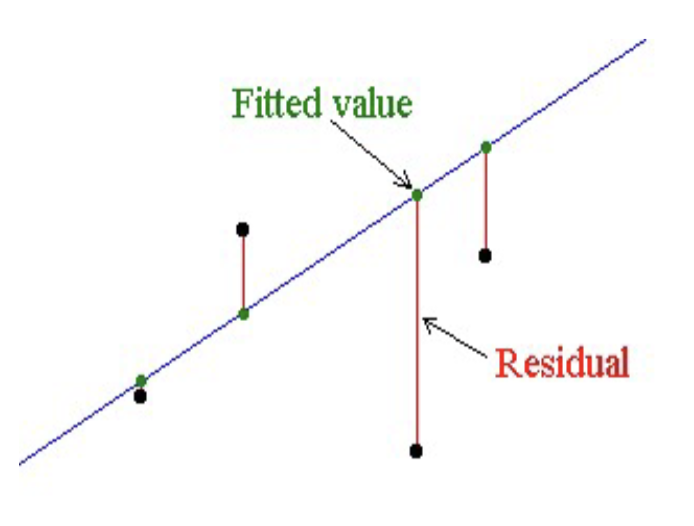
因此，我们需要通过对α和β求偏导并令其等于 0，来最小化上述函数，从而得到正规方程组，进而求出截距和回归系数的 “最佳拟合” 值

推导过程

Problem sheet – Weeks 8-9 例题1（已复习0次）

1.5 Fitted values and residuals, residual variance 拟合值、残差与残差方差

拟合值Fitted value：与观测自变量\(X_i\)相对应的最佳拟合直线上的点。

残差：真实值与拟合值之间的差值\(Y_i – \hat{Y}_i\)

可以利用残差来估计模型方差\(\sigma^2\)：

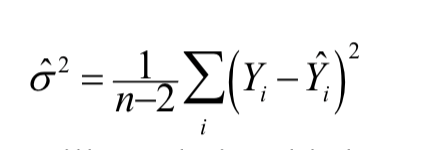
Problem sheet – Weeks 8-9 例题3（已复习0次）

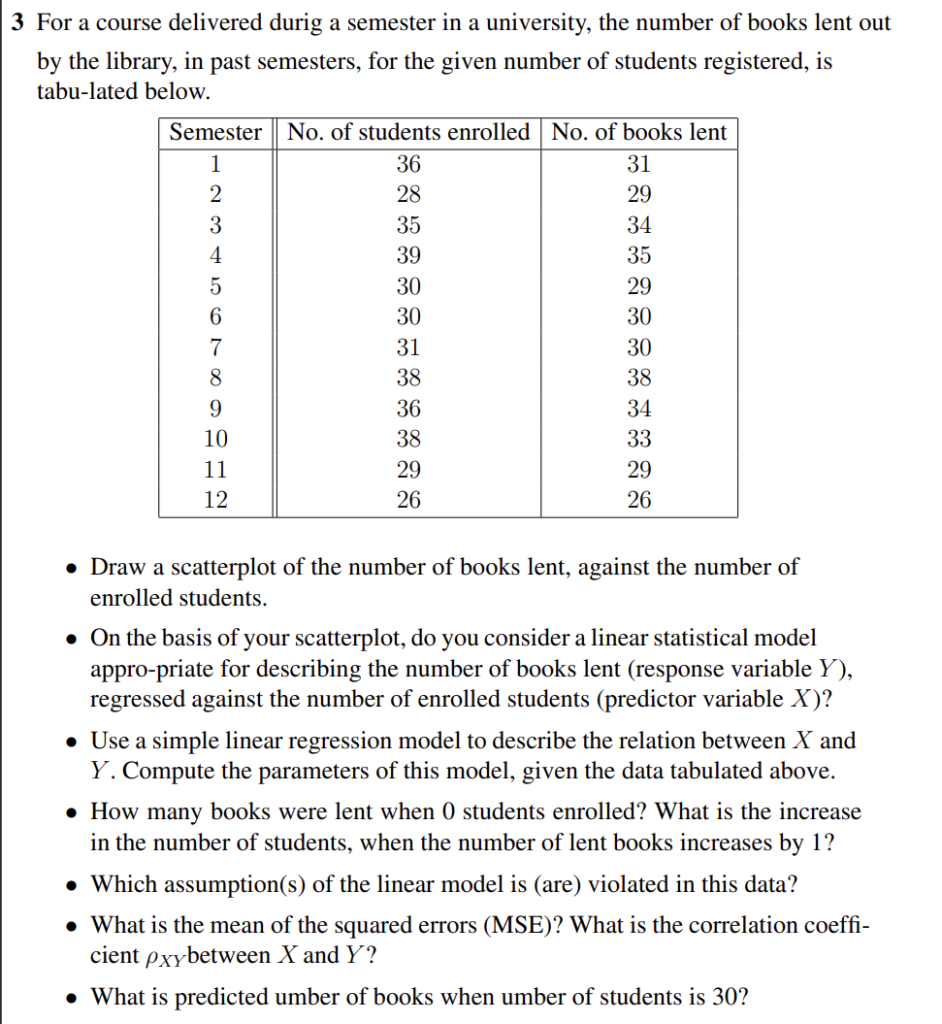
1.6 实例分析

研究问题为：会计学成绩（以测试分数衡量）是否会影响统计学成绩？
在本分析中，我们将会计学成绩视为固定变量（自变量），将统计学成绩视为因变量（或待预测的结果），首先确定描述会计学成绩与统计学成绩之间关系的模型，进而对统计学成绩进行预测

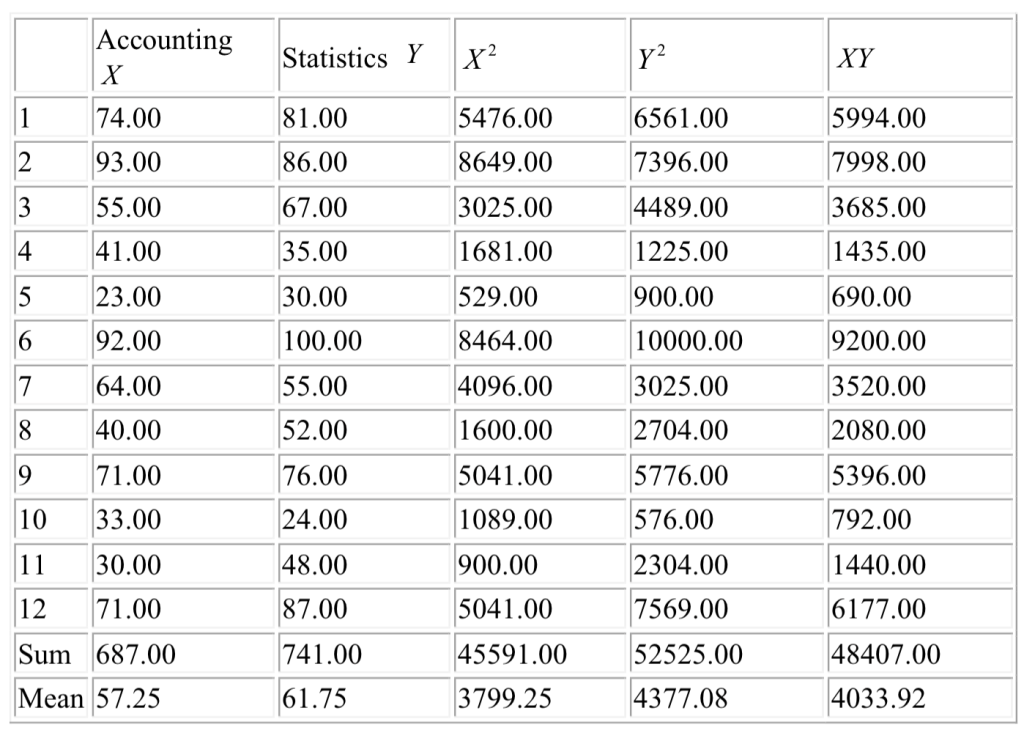
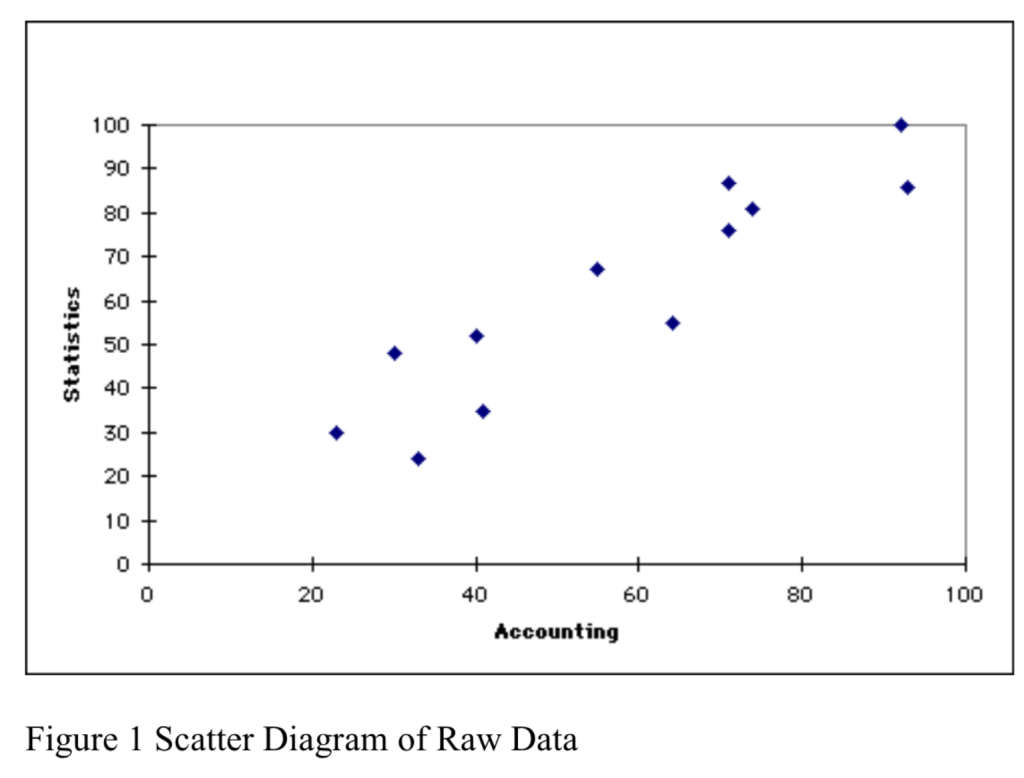
系数说明了什么：7.0194 是当会计（Accounting）的成绩为 0 时，统计学（Statistics）成绩的估计平均值，当会计成绩每增加 1 个单位时，统计学成绩会增加大约 0.956 个单位

\(\hat{Y}\)代表什么：\(\hat{Y}\)是在给定会计成绩X的条件下，用来估计统计学成绩Y的均值\(E(Y)\)的一个估计量（预测值 / 估计值）

代码实现：

# 数据框accdata的结构与内容：包含自变量X和因变量Y两列，共12行观测数据
accdata
## X  Y
## 1  74 81
## 2  93 86
## 3  55 67
## 4  41 35
## 5  23 30
## 6  92 100
## 7  64 55
## 8  40 52
## 9  71 76
## 10 33 24
## 11 30 48
## 12 71 87

# 计算拟合值Yhat：根据回归方程 Yhat = 截距 + 斜率*X 计算
# 其中截距为7.019，斜率为0.956，自变量X取自数据框accdata的X列
fitted.Y <- 7.019 + 0.956 * accdata$X  
# 显示拟合值结果
fitted.Y  

# 计算残差：残差 = 因变量观测值(Y) - 拟合值(Yhat)
resid <- accdata$Y - fitted.Y  
# 显示残差结果
resid  
0.9935.029-13.203  # 此处为数据显示格式残留，无实际代码意义
## [1] 3.237 -9.927 7.401 -11.215 0.993 5.029 -13.203 6.74   6.74  
## [9] 1.105 -14.567 12.301 12.105 

# 绘制观测值散点图：横轴为自变量X，纵轴为因变量Y的实际观测值
plot(accdata$X, accdata$Y)  
# 在散点图上叠加拟合值点，用"X"符号标记拟合值位置
points(accdata$X, fitted.Y, pch="X")  
# 添加回归直线：参数分别为截距7.019和斜率0.956，直观展示回归趋势
abline(7.019, 0.956)  

1.7 拟合优度与决定系数 Goodness of fit and Coefficient of Determination

决定系数，通常称为\(R^2\) ，其含义是衡量 “模型解释了多少 Y 的波动”

总方差 / 总变异：度量围绕均值 \(\bar{y}\) 的总波动”（总离差平方和）

\(\text{SST} = \sum_{i=1}^n (y_i – \bar{y})^2\)

简单线性模型用预测值解释相对均值的波动（回归平方和）

\(\text{SSR} = \sum_{i=1}^n (\hat{y}_i – \bar{y})^2\)

3）“解释不了的部分” 是什么？

真实值和预测值之间还有差距（残差），这就是模型没解释到的波动（残差平方和）。

\(\text{SSE} = \sum_{i=1}^n (y_i – \hat{y}_i)^2\)

并且有分解关系：

\(\text{SST} = \text{SSR} + \text{SSE}\)

4）所以 \(R^2\) 就是 “解释比例”

\(R^2 = \frac{\text{SSR}}{\text{SST}} = 1 – \frac{\text{SSE}}{\text{SST}}\)

• \(R^2 = 0.8\)：表示 Y 的总波动里，大约 80% 能用 “X 与 Y 的线性关系” 解释，剩下 20% 属于噪声、遗漏变量、非线性关系等。

其计算公式为：

需要注意的是，在简单线性回归（即仅含一个自变量）的情况下，决定系数等于相关系数的平方\(r^2\)

相关系数和决定系数的对称性说明：
回归系数和相关系数之间存在简单的数学关系。需要注意的是，相关系数在X和Y之间是对称的，而回归系数则不具有对称性（这是因为回归模型是在X取固定值的条件下对Y进行建模）但在简单线性回归模型中，决定系数R2（即方差解释百分比）在X和Y之间也是对称的。因此，在比较两个连续变量时，方差解释百分比并不受自变量和因变量选择的影响

# 计算残差平方和（SSresid）：将每个残差平方后求和，反映模型未解释的变异
SSresid <- sum( (resid)^2 )  
# 输出残差平方和结果
SSresid  
## [1] 1046.876 

# 计算因变量Y的均值（Ybar）
mean(accdata$Y)  
## [1] 61.75 

# 计算总平方和（SStotal）：Y的观测值与均值的差的平方和，反映Y的总变异
SStotal <- sum( (accdata$Y - 61.75)^2 )  # 注：原代码中“–”为全角符号，建议替换为半角“-”
# 输出总平方和结果
SStotal  
## [1] 6768.25 

# 计算回归平方和（SSexplained）：拟合值与Y均值的差的平方和，反映模型解释的变异
SSexplained <- sum( (fitted.Y - 61.75)^2 )  
# 输出回归平方和结果
SSexplained  
## [1] 5721.468 

# 验证平方和分解关系：回归平方和 + 残差平方和 应近似等于总平方和（微小差异由四舍五入导致）
SSexplained + SSresid  
## [1] 6768.344 

# 计算决定系数R²：模型解释的变异占总变异的比例，衡量拟合优度
SSexplained/SStotal  
## [1] 0.8453393 

1.8 回归系数的假设检验（ Wald 检验）

到目前为止，尚未提及回归模型中任何变量的分布假设，仅讨论了给定X的条件下Y的条件期望和条件方差

可以证明回归系数β的（证明过程略）
期望：\(E(\hat{\beta}) = \beta\)
方差：\(\text{Var}(\hat{\beta}) = \frac{\sigma^2}{S_{XX}}\)

需要注意的是，计算该检验统计量时，需使用 1.5 节中定义的模型方差估计值：

\(\hat{\sigma}^2 = \frac{1}{n-2}\sum_i(Y_i – \hat{Y}_i)^2\)

一些当时提出的困惑

我记得样本方差不是方差公式前面乘n-1/1嘛，这里是什么意思？
答：\(\text{Var}(\hat{\beta})\)是回归系数估计量\(\hat{\beta}\)的方差（不是 “样本方差”），它的推导是基于回归模型的统计性质，和 “样本方差（估计总体方差）” 是不同的概念。
两者的区别是：

\(s^2 = \frac{1}{n-1}\sum (y_i – \bar{y})^2\)：是 ** 用样本估计 “总体y的方差”** 的公式。

\(\text{Var}(\hat{\beta}) = \frac{\sigma^2}{S_{xx}}\)：是回归系数估计量\(\hat{\beta}\)的方差；

系数不是就这有一个嘛，怎么还会有方差？
答：回归系数的 “真实值\(\beta\)” 是固定的，但 **“估计值\(\hat{\beta}\)” 是随样本变化的（因为样本是随机选的）**，所以\(\hat{\beta}\)是随机变量，自然有方差

接下来，我们思考如何判断Y和X之间是否存在关联
Wald 检验：如果Y和X之间不存在关联，那么回归系数β应为 0。

我们使用检验统计量\(\frac{\hat{\beta}}{SE(\hat{\beta})}\)来衡量反对原假设的证据强度（原文中 “1” 为多余字符，已删除）。

SE 是 Standard Error（标准误）的缩写
\(SE(\hat{\beta}) = \sqrt{Var(\hat{\beta})}\)

因此，检验统计量的计算公式为：

\(\frac{\hat{\beta}}{SE(\hat{\beta})} = \frac{S_{XY}}{S_{XX}}\sqrt{\frac{S_{XX}}{\hat{\sigma}^2}} = \frac{S_{XY}}{\sqrt{\hat{\sigma}^2 S_{XX}}}\)

为了计算原假设下检验统计量的分布，我们需要对数据的分布做出假设。假设残差服从正态分布（均值为 0，方差为\(\sigma^2\)），那么该检验统计量服从自由度为\(n – 2\)的 t 分布

总结流程：

设假设：
\(H_0: \beta = 0\)（没线性关系），\(H_1: \beta \neq 0\)（有线性关系）。
算统计量：
\(t = \frac{\hat{\beta}}{SE(\hat{\beta})}\)
意思是看\(\hat{\beta}\)离 0 有多少个 “标准误”。
看分布求 p 值 / 临界值：
在误差近似正态下，\(t \sim t_{n-2}\)。
下结论：
p 小于显著性水平（如 0.05）→ 拒绝\(H_0\)→\(\beta\)显著不为 0（有关系）；否则不拒绝

1.9 Introduction to Multiple Linear Regression 多元线性回归简介

我们来考虑这样一类实验场景：观测到的响应变量Y依赖于p个非随机变量x0​,x1​,…,xp−1​，这些变量被称为自变量independent、解释变量explanatory或协变量covariates。我们假设响应变量的均值（即响应变量的期望）与这些协变量之间满足以下方程

\[ \mathrm{E}(Y \mid X)=\beta_0 x_0 + \beta_1 x_1 + \dots + \beta_{p-1} x_{p-1} \ , \]

且在协变量所有取值下，响应变量的方差均保持恒定

此处，X代表由p个协变量x0​,x1​,…,xp−1​组成的集合

通常会令协变量x0​=1，这样就能在模型中引入截距项

需要注意的是，我们所构建的模型描述的是响应变量Y在给定协变量X条件下的条件均值和条件方差

该模型被称为线性模型，原因是Y的期望被建模为解释变量x0​,x1​,…,xp−1​的线性函数

模型中的参数β0​,β1​,…,βp−1​被称为回归系数 regression coefficient

由于我们将预测变量视为固定变量，因此可以基于X的任意函数进行条件建模。我们可将其理解为定义一个对响应变量具有线性影响的新预测变量，例如设U=exp(−X2)，此时X与Y之间的关系模型可转化为：

\[ E(Y \mid U = u) = \beta_0 + \beta_1 \exp\left(-x(u)^2\right) = \beta_0 + \beta_1 u \]

1.10 Multiple Linear Regression Model with Data

假设我们对响应变量进行了n次独立观测，得到观测值\(Y_1,Y_2,\dots,Y_n\)，对应的协变量取值分别为\((x_{01},x_{11},\dots,x_{p-1,1})\)、\((x_{02},x_{12},\dots,x_{p-1,2})\)、…、\((x_{0n},x_{1n},\dots,x_{p-1,n})\)。

变量说明：

Fitted values 拟合值

residuals残差

反应模型的预测误差

RSS：Residual Sum of Squares 残差平方和

记巧：残差的平方和，肯定是残差的定义：真实值 – 预测值（没平均值的事情）

residual variance 残差方差

公式就是把所有点的残差加起来再取平均（要减去消耗的自由度）

TSS：Total Sum of Squares 总平方和 – 所有数据点偏离平均值的总乱度（离均值平方和）

数据的真实值 – 平均值

ESS：（课外）Explained sum of squares 回归平方和

数据的预测值 – 数据的平均值

Regression Coefficient 回归系数

Coefficient of determination 决定系数

在简单线性回归（即仅含一个自变量）的情况下，决定系数等于相关系数的平方r2。

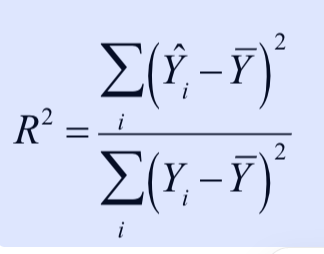
Correlation Coefficient相关系数（ r）

相关系数在X和Y之间是对称的，而回归系数则不具有对称性（这是因为回归模型是在X取固定值的条件下对Y进行建模）

Sample Standard Deviation of X 样本标准差 和样本协方差

Sum of Squares of X deviations 离差的平方和

离差 = 一个数据点 与 全体平均值 的差

\(S_{XX}\)	自变量 x 的离均差平方和	\(\sum (x_i – \bar{x})^2\)	衡量自变量 x 自身的变异（离散）程度
\(S_{XY}\)	自变量 x 与因变量 y 的离均差乘积和	\(\sum (x_i – \bar{x})(y_i – \bar{y})\)	衡量 x 与 y 之间的线性关联方向与程度
\(S_{YY}\)	因变量 y 的离均差平方和	\(\sum (y_i – \bar{y})^2\)	衡量因变量 y 自身的变异（离散）程度

“离均差平方和” 是统计学中衡量一组数据离散程度的指标，核心是先算每个数据与平均值的差（离均差），再平方，最后把这些平方值加起来

TSS ESS RSS 直观理解

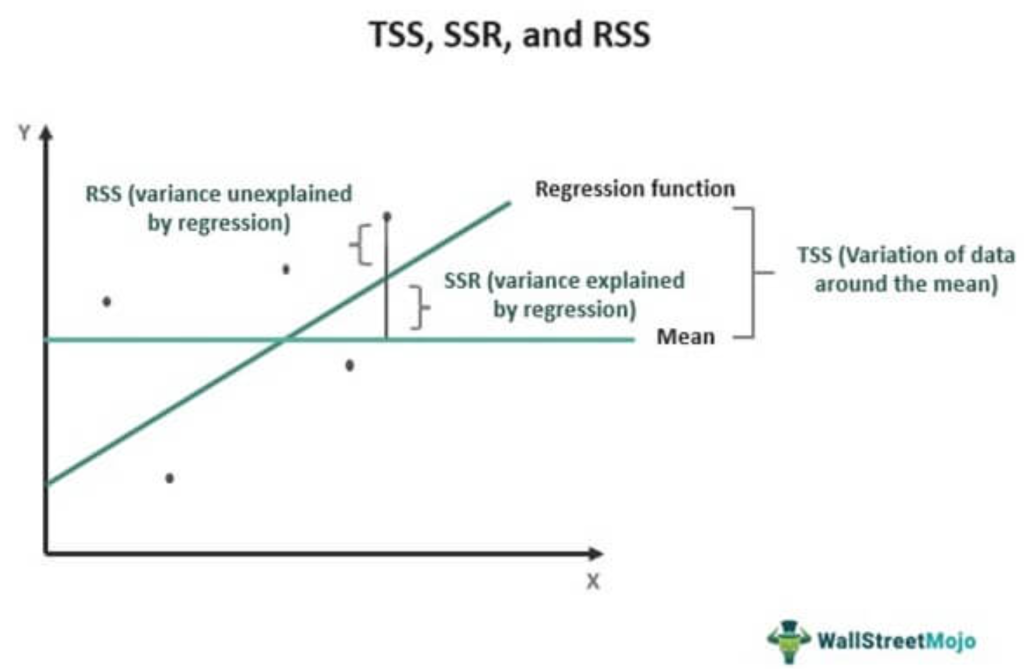
• TSS：每个点离均值的距离（数据本身的总变动）
• ESS：预测值（回归线）离均值的距离（模型解释部分）
• RSS：点离预测值的距离（模型未解释部分）