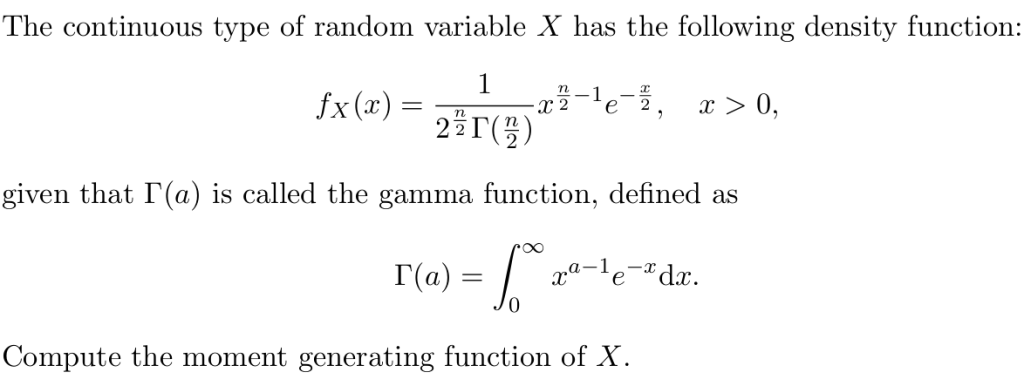Reference:
拉普拉斯变换与拉普拉斯逆变换的常用结论与经典公式-CSDN博客
拉普拉斯变换时傅里叶变换的泛化版本,傅里叶变换可用于
傅里叶变换除了处理信号外,还可以用于做很多其他事情,比如解微分方程,利用对函数n阶导的傅里叶变换等于其傅里叶变换乘以iw的n次方,能将微分方程变为简单的代数方程,再通过傅里叶逆变换就可以得到y(t)的解析式,微分方程得解。后来我才体会到变换求解微分方程的重要性,还记得解二阶常系数非齐次微分方程,当时规定右侧只能为P(X)e^rx和另一种共两种形式的公式,但如果当时学会拉普拉斯变换,右侧无论什么函数都可以求解。

但傅里叶变换要求函数满足狄利克雷条件,之前的习题通过限制范围或应用限制函数使其满足条件,因此可以在y轴上对其积分,得到特定频率下的幅值。但这肯定与真实结果不符。现实中的很多信号并不是有界的,许多基础函数比如指数函数、常函数、幂函数都是发散的,如果需要对这些发散信号/函数的频谱分析,
并且傅里叶变换能很好地告诉我们函数中存在哪些正弦曲线,但是不能表示其衰减的属性,而自然界中的信号都是符合指数衰减模型。
公式
注意积分下限变为0,可以理解为为了防止积分结果趋于无穷,在下面的例题中可以感受这一点

回顾时域->频域->复频域

常用拉普拉斯变换

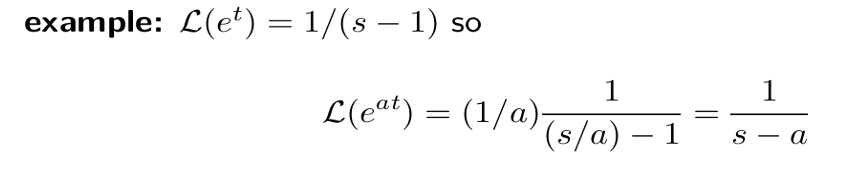
贴一个证明过程,如果忘了公式可以现场推导


性质

性质9:

注意区分线性性质和相似(放缩)性质:


n阶导的拉普拉斯变换有n+1项
常用结论的例题
性质9

性5:

性质1:
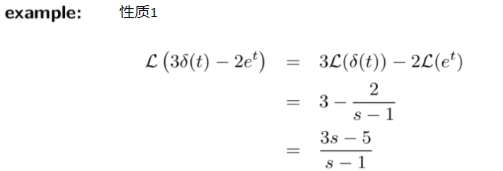
性质8:
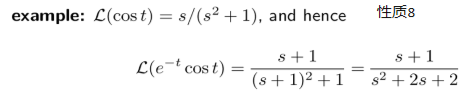

常用结论的例题

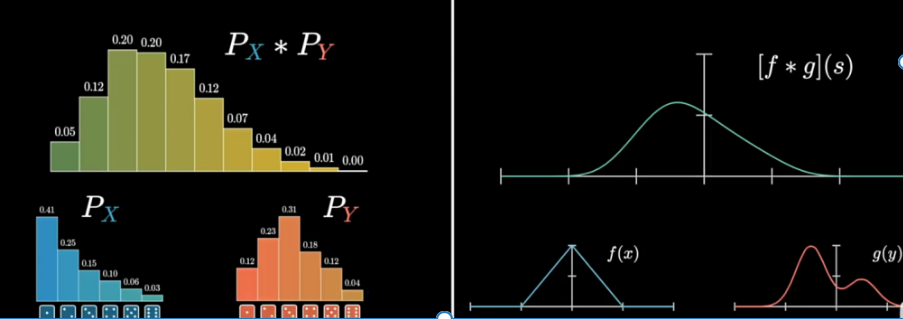
卷积
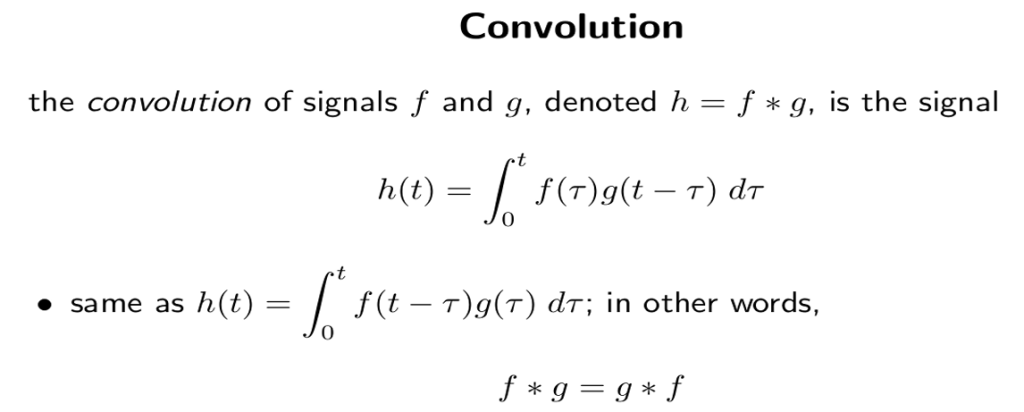

拉普拉斯变换解微分方程
拉普拉斯变换将微分运算转换为代数运算(乘以 s),对每一项单独应用拉普拉斯变换。因此我们最终得到了关于 Y(s)的简单代数方程。最后一步(通常也是最复杂的一步)是从 Y(s)还原 y(t)



伽马函数计算非整数阶乘
对于非整数 \( z \),在非负实数域上,阶乘计算用 Gamma function(亦称 \(\Gamma\) 函数)扩展:
\[
z! = \Gamma(z+1) = \int_0^\infty t^z e^{-t} \, dt
\]伽马函数满足递推公式:
\[
\Gamma(x+1) = x \Gamma(x)
\]

概率与统计中的拉普拉斯变换
期望 expectation
是试验中每次可能结果的概率乘以其结果的总和,反映随机变量平均取值的大小(与平均值含义相同)大数定律表明,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值
离散型随机变量 \( X \) 的期望:
\[
E(X) = \sum_i x_i \cdot P(X = x_i)
\]连续型随机变量 \( X \) 的期望:
\[
E(X) = \int_{-\infty}^{+\infty} x f(x) \, dx
\]
离散型随机变量:
\[
E(Y) = E[g(X)] = \sum_{k=1}^\infty g(x_k) p_k
\]
连续型随机变量:
\[
E(Y) = E[g(X)] = \int_{-\infty}^{+\infty} g(x) f(x) \, dx
\]
二元离散型随机变量 \( \mathbf{Z} = g(\mathbf{X}, \mathbf{Y}) \):
\[
E(Z) = E[g(X,Y)] = \sum_i \sum_j g(x_i, y_j) p_{ij}
\]
二元连续型随机变量:
\[
E(Z) = E[g(X,Y)] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x,y) f(x,y) \, dx \, dy
\]
常用分布的期望与方差

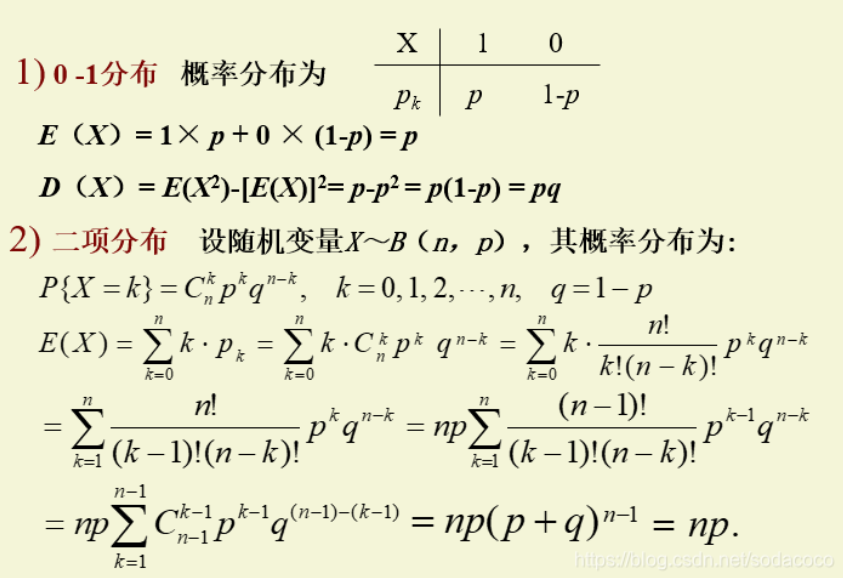



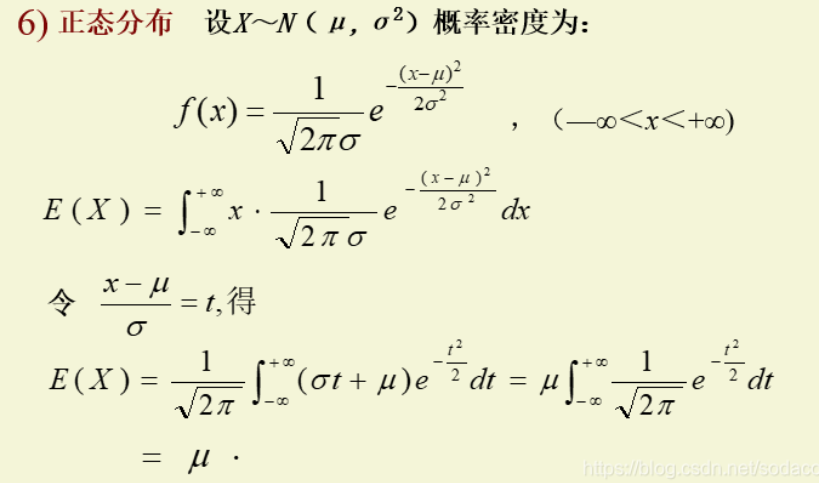

矩 Moment
矩(moment)是对变量分布和形态特点的一组度量。n阶矩通常用符号μn表示,n阶指的是随机变量X的多少次方。矩可以理解为距离的意思,一个随机变量的原点矩就是与所有样本与原点的距离之和的平均值,一个随机变量的中心矩为每个样本到样本平均值的距离之和的平均值
原点矩
设X为随机变量,k为正整数,则称 \(E(X^k)\)为随机变量X的k阶原点矩,记为 \(v_k\),\(k=1,2,\dots\)
离散型原点矩\[ v_k = \sum_{i=1}^n x_i^k p_i \]连续型原点矩\[ v_k = \int_{-\infty}^{+\infty} x^k f(x) \, dx \]
- 如果函数表示质量,则一阶原点矩为质心
- 如果函数是概率分布,那么一阶原点矩就是随机变量X全部取值的期望值(期望值 = 均值)。高阶原点矩的含义是对N阶的随机变量求均值
中心矩
设X为随机变量,k为正整数,则称 \(E[(X – EX)^k]\) 为随机变量X的k阶中心矩,\(k=1,2,\dots\)。显而易见:一阶中心矩等于0,二阶中心矩就是方差DX。
离散型中心矩\[ \mu_k = \sum_{i=1}^n (x_i – EX)^k p_i \]连续型中心矩\[ \mu_k = \int_{-\infty}^{+\infty} (x – EX)^k f(x) \, dx \]
EX表示随机变量 X 的期望值(Expectation),也称为均值,所以也可写做\(\bar{X}\)
- 任何随机变量的一阶中心矩为0
- 如果函数表示质量,二阶中心矩为转动惯量
- 如果函数是概率分布,二阶中心矩是方差variance,三阶中心矩是偏度skewness,四阶中心矩是峰度kurtosis。
- 对于二阶及更高阶的矩,通常使用中心矩,而不是原点矩,因为中心矩能更清楚的体现关于函数图像分布/图形形状的信息。
矩生成函数(MGF)Moment Generation Function
矩生成函数是用来寻找矩的函数的函数,实际上是一个 Laplace 变换。矩生成函数是随机变量概率分布的另一种描述方式。相较于直接使用概率质量函数/概率密度函数(两种概率函数的讲解见这里进行分析,它提供了一条替代路径来获得解析结果。
补充:
- 实值函数:函数输出值是实数的函数
- 实变函数:函数输入参数是实数的函数 复变函数:函数输入参数是复数的函数
- 生成函数:函数输出值是一个函数,对于Laplace变换,输入函数 x(t) 。 输出一个关于复数变量 s 的函数 X(s)
定义
设 \( X \) 为一个随机变量。矩生成函数}定义为:\[
M(t) = M_X(t) := E[e^{tX}]
\]
当 \( X \) 为离散型时,可表示为:\[
M(t) = \sum_{x} e^{tx} p_X(x)
\]因此,\( M(t) \) 是多个指数函数的加权平均。
当 \( X \) 为连续型时,可表示为:
\[
M(t) = \int_{-\infty}^{\infty} e^{tx} f(x) \, dx
\] 因此,\( M(t) \) 是连续指数函数的加权平均。
性质:
性质1:如果两个随机变量X具有相同的矩生成函数,则两个X具有相同的分布
性质2:\(M(0) = 1\)
性质3:矩与矩生成函数的关系
X 的N阶原点矩等于其矩生成函数 \( M_X(t) \) 在t = 0处的N阶导数值。
\[M _ { X } ^ { ( N ) } ( 0 ) = E [ X ^ { N } ]\]
验证:\[
M'(0) = \left[ \frac{d}{dt} \mathbb{E} e^{tX} \right]_{t=0}
= \mathbb{E} \left[ \frac{d}{dt} e^{tX} \right]_{t=0}
= \mathbb{E} \left[ X e^{tX} \right]_{t=0}
= \mathbb{E}(X)
\]实际上对于 \( k \) 阶导,\(M^{(k)}(0) = \mathbb{E}(X^k)\)利用这一性质,我们可以很方便地计算一个分布的任意阶矩。如果知道 \( M \) 在某一点的所有导数,即可得到所有整数 \( k \geq 0 \) 的矩 \( E[X^k] \)。
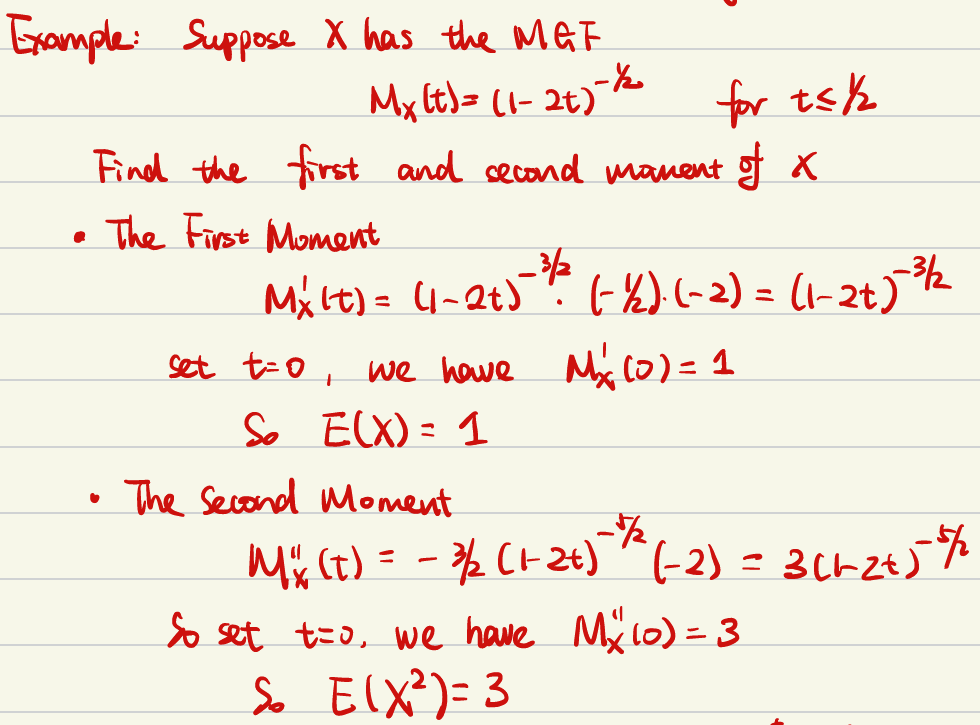
性质4:独立随机变量的和的矩生成函数,等于各自矩生成函数的乘积\[
M_{X_1 + X_2 + \cdots + X_n}(t) = M_{X_1}(t) \cdot M_{X_2}(t) \cdots M_{X_n}(t)
\]
验证:设 \( X \) 和 \( Y \) 为独立随机变量当Z = X + Y
矩生成函数分别为\[ M_X(t) = E[e^{tX}] \] \[ M_Y(t) = E[e^{tY}] \] \[ M_Z(t) = E[e^{tZ}] \]
由独立性可得
\[
M_Z(t) = E[e^{t(X+Y)}] = E[e^{tX}e^{tY}] = E[e^{tX}]E[e^{tY}] = M_X(t)M_Y(t)
\]
性质5:线性变换性质
若 \( Z = aX \),用 \( M_X \) 表示 \( M_Z \)
\[ M_Z(t) = E[e^{tZ}] = E[e^{taX}] = M_X(at) \]
若 \( Z = X + b \),用 \( M_X \) 表示 \( M_Z \)
\[ M_Z(t) = E[e^{tZ}] = E[e^{tX+bt}] = e^{bt} M_X(t) \]
以下几种典型分布时的矩生成函数:
二项分布的MGF公式证明
当 X 服从参数为 (p,n)的二项分布时,n:试验的总次数(正整数)。p:每次试验成功的概率(0≤p≤1)
矩生成函数为:
\[
M_X(t) = E[e^{tX}] = e^{t \cdot 1} \cdot P(X = 1) + e^{t \cdot 0} \cdot P(X = 0) = e^t \cdot p + e^0 \cdot (1 – p) = pe^t + (1 – p)
\]\[
M_X(t) = pe^t + 1 – p
\]
泊松分布的MGF公式证明
若 X 服从参数为 λ>0的泊松分布

\[ M_{X}(t) = E[e^{tX}] = \sum_{n=0}^{\infty} e^{tn} P(X = n) \]
将泊松分布的 PMF 代入 MGF 的定义: \[ M_X(t) = \sum_{n=0}^{\infty} e^{tn} \cdot \frac{e^{-\lambda}\lambda^n}{n!} \]
提取常数 \(e^{-\lambda}\): \[ M_X(t) = e^{-\lambda} \sum_{n=0}^{\infty} \frac{e^{tn}\lambda^n}{n!} \]
合并指数项 \(e^{tn}\lambda^n\):
\[
e^{tn}\lambda^n = (e^t\lambda)^n
\]\[
M_X(t) = e^{-\lambda} \sum_{n=0}^{\infty} \frac{(e^t\lambda)^n}{n!}
\]
识别泰勒级数(指数函数的展开式)\[
e^x = \sum_{n=0}^\infty \frac{x^n}{n!}
\]\[
\sum_{n=0}^\infty \frac{(e^t \lambda)^n}{n!} = e^{\lambda e^t}
\]\[
M_X(t) = e^{-\lambda} \cdot e^{\lambda e^t} = e^{\lambda e^t – \lambda} = \exp[\lambda(e^t – 1)]
\]
泊松分布的矩生成函数为:
\[
M_X(t) = \exp[\lambda(e^t – 1)]
\]


从上述示例可以看出,矩生成函数并不需要对所有t值都有定义。例如,指数型随机变量的矩生成函数仅当 t≤1/λ 时成立(后面的例1也有提到)

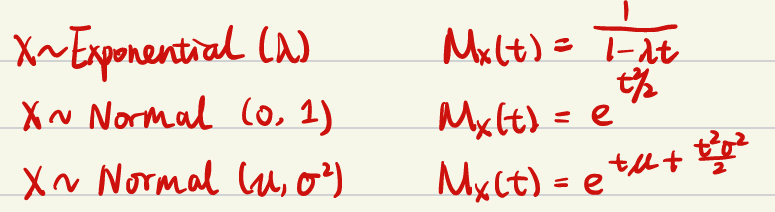
例题:
例1:需要对t进行限制保证积分结果是收敛

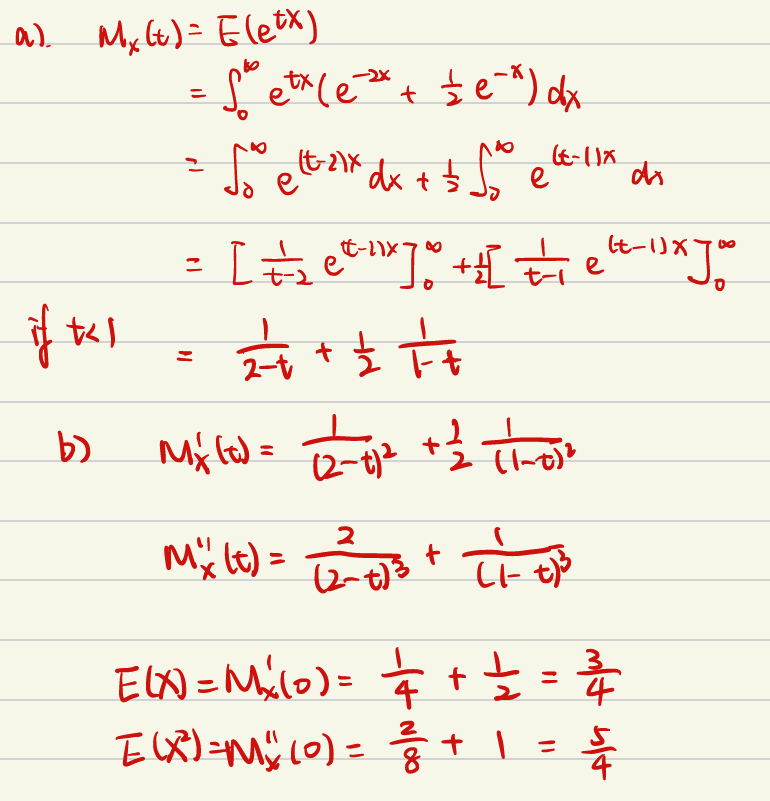
矩生成函数 MX(t)的计算结果仅在参数 t的特定范围内有效(即收敛域)。当 t超出该范围时,积分发散导致 MX(t)无意义(趋于无穷)
例2:

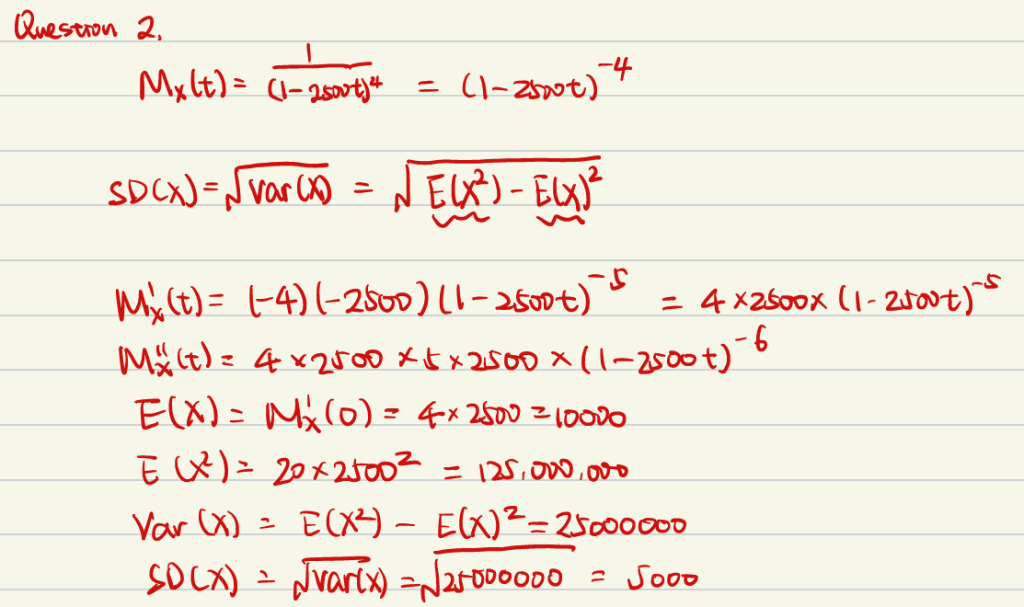
例3:矩生成函数性质
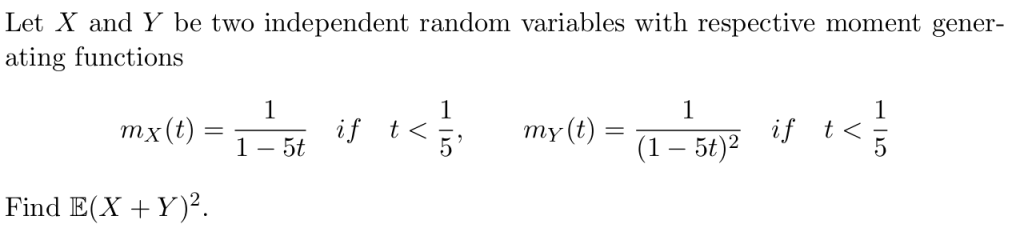
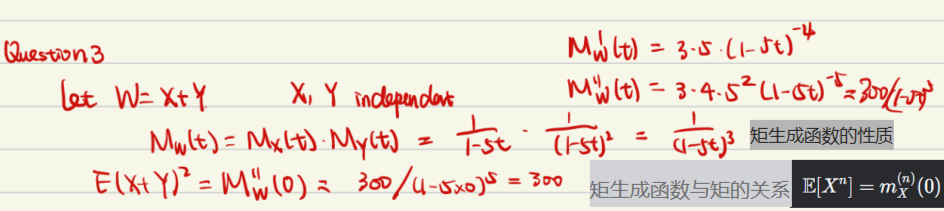
例4:

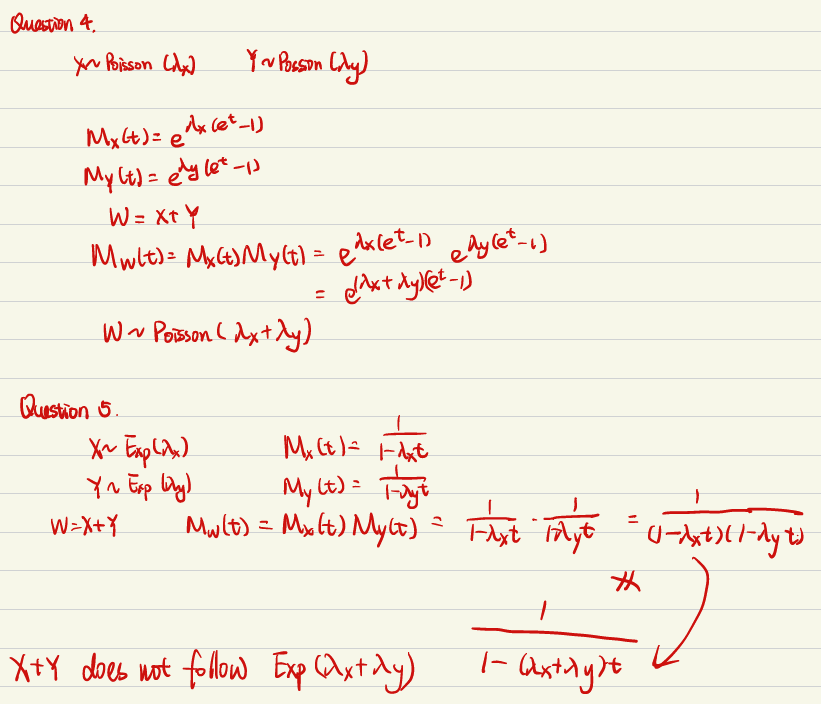
例5: