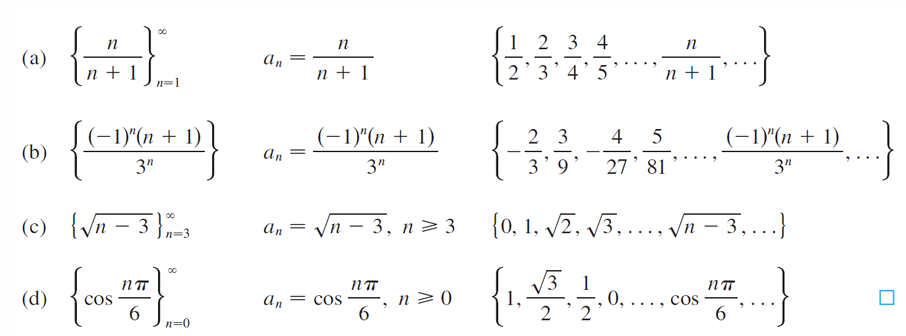在定义定积分时，我们处理的是在有限区间 [a,b]上定义的函数 f，并且假设f在该区间内没有无限间断点(瑕点)

Infinite Intervals 无穷限的反常积分

对于函数 \( f(x) \)，如果对于每一个 \( t \geq a \)，积分 \( \int_a^t f(x) \, dx \) 都存在，那么反常积分 \( \int_a^\infty f(x) \, dx \) 定义为极限 \[ \int_a^\infty f(x) \, dx = \lim_{t \to \infty} \int_a^t f(x) \, dx, \] 前提是该极限存在且为有限数。

类似地，如果对于每一个 \( t \leq b \)，积分 \( \int_t^b f(x) \, dx \) 都存在，那么反常积分 \( \int_{-\infty}^b f(x) \, dx \) 定义为极限
\[
\int_{-\infty}^b f(x) \, dx = \lim_{t \to -\infty} \int_t^b f(x) \, dx,
\]
前提是该极限存在且为有限数。

如果上述极限存在且为有限数，则称反常积分收敛；如果极限不存在，则称反常积分发散。从面积的角度就是如果函数图像下的面积是有限的，则积分收敛，反之则发散

如果 \( \int_a^\infty f(x) \, dx \) 和 \( \int_{-\infty}^a f(x) \, dx \) 都收敛，那么全区间反常积分 \( \int_{-\infty}^\infty f(x) \, dx \) 定义为这两个积分的和： \[ \int_{-\infty}^\infty f(x) \, dx = \int_{-\infty}^a f(x) \, dx + \int_a^\infty f(x) \, dx. \]

Discontinuous Integrals (无界函数的反常积分)瑕积分

对于类型1积分，区域在水平方向上无限延伸。这里区域在垂直方向上无限延伸

(a) 如果 \( f \) 在 \([a, b]\) 上连续，并且在 \( b \) 处间断，则
\[
\int_{a}^{b} f(x) \, dx = \lim_{t \to b^{-}} \int_{a}^{t} f(x) \, dx
\]
前提是该极限存在（为一个有限数）。

(b) 如果 \( f \) 在 \((a, b]\) 上连续，并且在 \( a \) 处间断，则
\[
\int_{a}^{b} f(x) \, dx = \lim_{t \to a^{+}} \int_{t}^{b} f(x) \, dx
\]
前提是该极限存在（为一个有限数）。

反常积分 \(\int_{a}^{b} f(x) \, dx\) 如果相应的极限存在，则称为收敛。如果极限不存在，则称为发散

(c) 如果 \( f \) 在 \( c \) 处有间断，其中 \( a < c < b \)，且 \(\int_{a}^{c} f(x) \, dx\) 和 \(\int_{c}^{b} f(x) \, dx\) 都收敛，则我们定义
\[
\int_{a}^{b} f(x) \, dx = \int_{a}^{c} f(x) \, dx + \int_{c}^{b} f(x) \, dx
\]

例题

example1 Evaluate \( \int_{0}^{3} \frac{dx}{x-1} \) if possible.

SOLUTION Observe that the line \( x = 1 \) is a vertical asymptote of the integrand. Since it occurs in the middle of the interval \([0, 3]\), we must use part (c) of Definition 3 with \( c = 1 \):
$$
\int_{0}^{3} \frac{dx}{x-1} = \int_{0}^{1} \frac{dx}{x-1} + \int_{1}^{3} \frac{dx}{x-1}
$$
where
$$
\int_{0}^{1} \frac{dx}{x-1} = \lim_{t \to 1^{-}} \int_{0}^{t} \frac{dx}{x-1} = \lim_{t \to 1^{-}} \ln |x-1| \bigg|_{0}^{t}
$$
$$
= \lim_{t \to 1^{-}} (\ln |t-1| – \ln |-1|)
$$
$$
= \lim_{t \to 1^{-}} \ln (1-t) = -\infty
$$
because \( 1-t \to 0^+ \) as \( t \to 1^- \). Thus \( \int_{0}^{1} \frac{dx}{x-1} \) is divergent. This implies that \( \int_{0}^{3} \frac{dx}{x-1} \) is divergent. [We do not need to evaluate \( \int_{1}^{3} \frac{dx}{x-1} \)

如果我们没有注意到渐近线 x=1x=1，而是将积分误认为是普通积分，那么我们可能会做出以下错误的计算：\[
\int_{0}^{3} \frac{dx}{x-1} = \ln |x-1| \bigg|_{0}^{3} = \ln 2 – \ln 1 = \ln 2
\]

这是错误的，因为积分是反常的，必须通过极限来计算。
从现在开始，每当你遇到符号 \( \int_a^b f(x) \, dx \) 时，必须通过观察函数 \( f \) 在 \([a, b]\) 上的情况来决定它是普通定积分还是反常积分。

example2：计算 \(\int_{0}^{1} \ln x \, dx\)。

解：我们知道函数 \(f(x) = \ln x\) 在0处有一个垂直渐近线，因为 \(\lim_{x \to 0^+} \ln x = -\infty\)。因此，给定的积分是反常的，我们有
\[
\int_{0}^{1} \ln x \, dx = \lim_{t \to 0^+} \int_{t}^{1} \ln x \, dx
\]

现在我们通过分部积分，设 \(u = \ln x, \, dv = dx, \, du = \frac{dx}{x}, \, v = x\)：
\[
\int_{t}^{1} \ln x \, dx = x \ln x \bigg|_{t}^{1} – \int_{t}^{1} dx = 1 \ln 1 – t \ln t – (1 – t) = -t \ln t – 1 + t
\]

为了找到第一项的极限，我们使用洛必达法则：
\[
\lim_{t \to 0^+} t \ln t = \lim_{t \to 0^+} \frac{\ln t}{1/t} = \lim_{t \to 0^+} \frac{1/t}{-1/t^2} = \lim_{t \to 0^+} (-t) = 0
\]

因此
\[
\int_{0}^{1} \ln x \, dx = \lim_{t \to 0^+} (-t \ln t – 1 + t) = -0 – 1 + 0 = -1
\]

反常积分的敛散检验

有时无法找到反常积分的精确值，但知道它是收敛还是发散仍然很重要。尽管我们针对类型1积分陈述了它，但对于类型2积分也有类似的定理。

比较定理 假设 \( f \) 和 \( g \) 是连续函数，且
\[
f(x) \geq g(x) \geq 0 \text{ 对于 } x \geq a.
\](a) 如果 \(\int_a^\infty f(x) \, dx\) 收敛，则 \(\int_a^\infty g(x) \, dx\) 收敛（收找大 证小）
(b) 如果 \(\int_a^\infty g(x) \, dx\) 发散，则 \(\int_a^\infty f(x) \, dx\) 发散。（散找小 证大）

例题：证明 \(\int_0^\infty e^{-x^2} \, dx\) 是收敛的。

解：如果我们尝试通过反常积分的极限定义来计算：
\[
\int_{0}^{\infty} e^{-x^2} \, dx = \lim_{b \to \infty} \int_{0}^{b} e^{-x^2} \, dx
\]但由于无法找到 \( e^{-x^2} \) 的反导数，因为 \(e^{-x^2}\) 的反导数(不定积分)不是初等函数，我们无法直接计算该积分。所以我们尝试证明其敛散性
\[
\int_0^\infty e^{-x^2} \, dx = \int_0^1 e^{-x^2} \, dx + \int_1^\infty e^{-x^2} \, dx
\]右边的第一个积分只是一个普通的定积分。在第二个积分中，我们利用对于 \(x \geq 1\) 有 \(x^2 \geq x\)，因此 \(-x^2 \leq -x\)，所以 \(e^{-x^2} \leq e^{-x}\)。（见图13。）\(e^{-x}\) 的积分很容易计算：
\[
\int_1^\infty e^{-x} \, dx = \lim_{t \to \infty} \int_1^t e^{-x} \, dx = \lim_{t \to \infty} (e^{-1} – e^{-t}) = e^{-1}
\]

因此，在比较定理中取 \(f(x) = e^{-x}\) 和 \(g(x) = e^{-x^2}\)，我们看到 \(\int_1^\infty e^{-x^2} \, dx\) 是收敛的。因此，\(\int_0^\infty e^{-x^2} \, dx\) 是收敛的。