核心思想： 假设检验是检验某个关于总体参数（比如均值、比例等）是否成立的方法。

统计假设： 是关于总体的一个猜测，比如“某产品的平均寿命是75小时”。

两种假设：

H₀（原假设）： 默认成立的假设。

Hₐ（备择假设）： 我们希望提供证据支持的假设。

例 1：假设我们希望评估一种新灯泡的平均寿命是否比当前型号更长，当前型号的平均寿命为 a。那么我们可能会检验：
\(H_{0}: \mu=a\quad \text{vs.}\quad H_{a}: \mu>a\)
这是一个单侧备择假设。相反，检验平均值是否在任一方向上与 a 不同：
\(H_{0}: \mu=a\quad \text{vs.}\quad H_{a}: \mu \neq a\)

决策过程与逻辑

假设检验是一种使用样本数据来决定是否拒绝 \(H_{0}\) 的程序，其逻辑如下：

1. 假设 \(H_{0}\) 为真。
2. 确定观察到与实际所见一样极端（或更极端）的数据的可能性有多大。
3. 如果这个概率很小，我们就拒绝 \(H_{0}\) 而支持 \(H_{a}\)。

定义 2：P 值是在假设零假设 \(H_{0}\) 为真的情况下，获得一个与观察到的检验统计量一样极端或更极端的概率。

解释：

• P 值越小，反对 \(H_{0}\) 并支持备择假设 \(H_{a}\) 的证据就越强。
• P 值量化了观察数据与 \(H_{0}\) 为真这一假设之间的不一致程度。

备注 1：需要注意的是，P 值不是 \(H_{0}\) 为真的概率，也不是从检验中得出的结论不正确的概率。相反，它是在 \(H_{0}\) 成立的假设下，数据极端程度的一种度量。

背景： 比较两个品牌酸奶 C 和 D，100人盲测选择喜好。

• 原假设 H₀：p = 0.5（没偏好）
• 观察到 37 人喜欢 C → 计算 P(X ≤ 37)，得出 P值 ≈ 0.006（非常小）
• 结论：拒绝 H₀，D 更受欢迎可能性大。

反例：如果 45 人喜欢 C，P值 ≈ 0.184（太大，不能拒绝 H₀）

显著性水平与检验规则

基于 P 值的决策规则

设 α 表示检验的显著性水平，这是我们愿意容忍的犯第一类错误（即当 \(H_{0}\) 为真时拒绝它）的最大概率。

决策规则：

• 如果 \(P \text{-value} \leq \alpha\)，拒绝 \(H_{0}\)。
• 如果 \(P \text{-value} > \alpha\)，不拒绝 \(H_{0}\)。

备注 5：α 的常见选择包括 0.05、0.01 和 0.001。α 的值越小，检验越严格。

假设我们计算出 \(P \text{-value}=0.0032\)，那么：

• 在 α=0.05 时：0.0032 < 0.05 ⇒ 拒绝 \(H_{0}\)。
• 在 α=0.01 时：0.0032 < 0.01 ⇒ 拒绝 \(H_{0}\)。
• 在 α=0.001 时：0.0032 > 0.001 ⇒ 不拒绝 \(H_{0}\)。

备注 6：P 值允许灵活的决策制定。较小的 P 值表示反对零假设的证据更强。

检验逻辑总结

1. 从明确的假设开始：\(H_{0}\) 和 \(H_{a}\)。
2. 选择适合数据类型和假设的检验统计量。
3. 从数据中计算统计量的观察值。
4. 确定检验统计量在 \(H_{0}\) 下的分布。
5. 计算相应的 P 值。
6. 将 P 值与显著性水平 α 进行比较，并决定：
   • 如果 P 值足够小（\(\leq \alpha\)），拒绝 \(H_{0}\)。
   • 否则，不拒绝 \(H_{0}\)。

这个框架构成了经典（频率论）假设检验的核心。

假设检验中的错误类型

进行假设检验时，可能会出现两种错误的结论：

• 第一类错误（α）：当 \(H_{0}\) 实际上为真时拒绝它。
• 第二类错误（β）：当 \(H_{0}\) 实际上为假时未能拒绝它。

例 3：一家谷物制造商声称其一种产品的一份含有 100 卡路里。由于生产可变性，每份的实际卡路里含量可能会有所不同。

我们希望检验消费者平均摄入的卡路里是否比声称的更多： \(H_{0}: \mu=100\quad \text{vs.}\quad H_{a}: \mu>100\)

背景中的错误类型：

• 第一类错误：得出平均卡路里含量超过 100 的结论，而实际上并没有。
• 第二类错误：未能检测到平均卡路里含量确实超过 100 的情况。

备注 7：原则上，完全消除这两种错误的唯一方法是观察整个总体。实际上，这是不可行的，我们必须使用样本并管理这些风险。

案例研究：Web 服务器弹性测试

假设在当前基础设施下，只有 25% 的模拟网络攻击使公司的 Web 服务器完全运行（即没有停机时间）。已经提出了一种新的服务器架构，并通过 n=20 次独立的模拟攻击试验进行评估。

我们检验： \(H_{0}: p=0.25\quad \text{vs.}\quad H_{a}: p>0.25\)

设 X 表示服务器保持完全运行的试验次数。在零假设 \(H_{0}\) 下，我们假设： \(X \sim Bin(20, 0.25), \quad \text{with} \quad \mathbb{E}[X]=20 \cdot 0.25=5\)

我们的目标是评估新架构是否比当前基线显著提高了弹性。

显著性水平和拒绝域

假设我们选择显著性水平 α=0.10，我们寻找能够提供反对 \(H_{0}\) 有力证据的 x 值。使用二项分布： \(\mathbb{P}(X \geq 7) \approx 0.214\) \(\mathbb{P}(X \geq 8) \approx 0.102\) \(\mathbb{P}(X \geq 9) \approx 0.041\)

为了确保检验的显著性水平约为 0.10，当 X≥8 时，我们拒绝 \(H_{0}\)。

第一类错误概率

定义 4：第一类错误概率（也称为显著性水平 α）为： \(\alpha=\mathbb{P}\left(\text{拒绝} H_{0} | H_{0} \text{为真}\right)=\mathbb{P}(X \geq 8 | X \sim Bin(20, 0.25)) \approx 0.102\)

备注 8：这意味着在重复抽样中，如果 \(H_{0}\) 为真，我们大约会在 10.2% 的此类实验中错误地拒绝零假设。考虑到我们选择的 α=0.10，这是一个可接受的风险。

第二类错误和功效分析

与第一类错误不同，没有单一的第二类错误概率，因为 \(H_{0}\) 可能以多种方式为假（例如，p=0.3，p=0.5 等）。

设 β(p) 表示当 p 的真实值大于 0.25 时未能拒绝 \(H_{0}\) 的概率。

示例：p=0.30 \(\beta(0.3)=\mathbb{P}(X \leq 7 | X \sim Bin(20, 0.3)) \approx 0.772\) 这意味着当真实成功概率为 0.30 时，有 77.2% 的概率未能检测到改进。

备注 9：真实 p 越接近 0.25，越难检测到差异，尤其是在样本量较小时。随着真实 p 的增加，检验的功效（即 1−β(p)）增加，即 β(p) 减小。

复合零假设和边界错误

假设我们不再希望检验简单的零假设 \(H_{0}: p=0.25\)，而是检验一个更现实的复合假设，例如： \(H_{0}: p \leq 0.25\quad \text{vs.}\quad H_{a}: p>0.25\)

在这种情况下，零假设包含 p 的多个值，而不仅仅是一个点。

• 对于每个值 \(p_{0} \leq 0.25\)，我们计算相应的第一类错误概率 α(\(p_{0}\))。
• 最大的第一类错误率发生在边界 p=0.25 处。
• 因此，如果显著性水平针对边界值进行控制，即 α(0.25)=0.102，那么对于所有 \(p_{0}<0.25\)，α(\(p_{0}\))<0.102。

备注 10：这确保了检验在更广泛的零假设下仍然有效。最坏情况下的第一类错误仍然与简化的点假设一致。

定理 1（显著性水平）：任何检验程序，如果 P 值≤α 时拒绝 \(H_{0}\)，否则不拒绝，其显著性水平为 α： \(\mathbb{P}(\text{第一类错误})=\alpha\)

定理 2（错误权衡）：设抽样程序、样本量 n 和检验统计量固定。那么增加显著性水平 α（即允许更大的拒绝 \(H_{0}\) 的机会）会导致对于任何备择假设 \(p \in H_{a}\)，第二类错误概率 β 减小。

含义：较大的 α 增加了拒绝 \(H_{0}\) 的机会，因此减少了错过真实效应的可能性（β 降低）。

备注 11：这种权衡意味着一个限制：除非增加样本量 n，否则不可能使 α 和 β 都任意小。

单侧检验的临界比例阈值

假设我们将显著性水平固定为 α，并检验右尾备择假设 \(H_{a}: p>p_{0}\)。如果样本比例超过阈值，我们拒绝零假设： \(\hat{p}_{\text{crit}}=p_{0}+z_{\alpha} \cdot \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}\) 这是在零分布下导致在 α 水平上拒绝 \(H_{0}\) 的最小样本比例。

双侧检验阈值

对于双侧备择假设 \(H_{a}: p \neq p_{0}\)，临界区域分布在正态分布的两个尾部。如果样本比例落在区间之外，我们拒绝零假设： \(\hat{p}<p_{0}-z_{\alpha / 2} \cdot \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}} \quad \text{或} \quad \hat{p}>p_{0}+z_{\alpha / 2} \cdot \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}\)

等价地，如果检验统计量的绝对值超过临界值，我们拒绝 \(H_{0}\)： \(|z|>z_{\alpha / 2}\) 这使得检验比单侧情况更保守，需要更强的证据来拒绝 \(H_{0}\)。

检验的功效（大样本近似）

为了评估检验检测真实备择假设 \(p=p_{1}\) 的能力，我们计算功效 1−β，它表示当备择假设为真时正确拒绝零假设的概率。

右尾检验：\(H_{0}: p=p_{0}\) vs. \(H_{a}: p>p_{0}\) 如果 \(\hat{p}>\hat{p}_{\text{crit}}\)，则拒绝 \(H_{0}\)，其中 \(\hat{p}_{\text{crit}}=p_{0}+z_{\alpha} \cdot \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}\)

则功效为： \(1-\beta=\mathbb{P}\left(Z>\frac{\hat{p}_{\text{crit}}-p_{1}}{\sqrt{p_{1}\left(1-p_{1}\right) / n}}\right)\)

左尾检验：\(H_{0}: p=p_{0}\) vs. \(H_{a}: p<p_{0}\) 如果 \(\hat{p}<\hat{p}_{\text{crit}}\)，则拒绝 \(H_{0}\)，其中 \(\hat{p}_{\text{crit}}=p_{0}-z_{\alpha} \cdot \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}\)

则功效为： \(1-\beta=\mathbb{P}\left(Z<\frac{\hat{p}_{\text{crit}}-p_{1}}{\sqrt{p_{1}\left(1-p_{1}\right) / n}}\right)\)

备注 12：该公式表明，功效随着以下因素的增加而增加：

• 更大的样本量 n
• 更大的效应量 \(|p_{1}-p_{0}|\)
• 更宽松的显著性水平 α

在研究设计中，通常目标是功效≥0.80。

双侧备择假设的检验功效

对于双侧假设 \(H_{0}: p=p_{0}\) vs. \(H_{a}: p \neq p_{0}\)，功效计算必须考虑分布的两个尾部。如果检验统计量落在临界值 ±\(z_{\alpha/2}\) 之外，我们拒绝零假设。

在备择假设 \(p=p_{1}\) 下，近似功效为： \(1-\beta=\mathbb{P}\left(Z<-z_{\alpha / 2} | p=p_{1}\right)+\mathbb{P}\left(Z>z_{\alpha / 2} | p=p_{1}\right)\)

即： \(1-\beta=\mathbb{P}\left(Z<\frac{p_{0}-z_{\alpha / 2} \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}-p_{1}}{\sqrt{\frac{p_{1}\left(1-p_{1}\right)}{n}}}\right)+\mathbb{P}\left(Z>\frac{p_{0}+z_{\alpha / 2} \sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}-p_{1}}{\sqrt{\frac{p_{1}\left(1-p_{1}\right)}{n}}}\right)\)

这评估了在备择假设 \(p_{1}\) 下，样本比例导致 \(\hat{p}\) 值落在 \(p_{0}\) 下定义的双尾拒绝区域之外的可能性。

备注 13：对于检测特定方向的变化，双侧检验的功效通常低于单侧检验，因为显著性水平 α 分布在两个尾部。在收集数据之前，始终根据科学背景选择检验方向。

例1：

一家微电子制造商历史上报告其一条微芯片生产线的缺陷率为 7%。最近，由于供应链中断和人员短缺，有人担心缺陷率可能已经上升。

为了评估当前缺陷率是否超过历史基准，质量控制分析师随机选择了 n=500 个上周生产的微芯片样本，发现其中 x=50 个有缺陷。

步骤 1：定义假设 我们将总体比例 p 定义为微芯片有缺陷的真实概率。假设为： \(H_{0}: p=0.07\quad \text{（历史缺陷率）}\) \(H_{a}: p>0.07\quad \text{（怀疑缺陷率增加）}\) 这是一个右尾检验，因为我们正在检验缺陷率是否增加。

步骤 2：检查正态近似条件 我们验证使用比例的大样本 z 检验的假设： \(n p_{0}=500 \cdot 0.07=35>5, \quad n\left(1-p_{0}\right)=500 \cdot 0.93=465>5\) 两个条件都满足，因此 \(\hat{p}\) 的抽样分布近似正态。

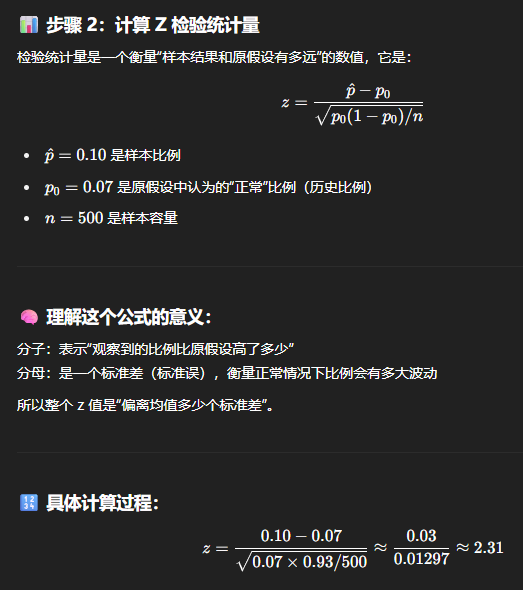
步骤 3：计算检验统计量

你有一个大样本（n = 500），观察到有 50 个“成功”事件（例如：50 个产品是坏的，或 50 人购买了商品等）。现在你想要检验观察到的比例（10%）是否显著大于历史比例（7%）。

步骤 4：计算 P 值 使用标准正态分布表或软件： \(P \text{-value} =\mathbb{P}(Z>2.31) \approx 0.0104\)

步骤 5：做出决策 将 P 值与显著性水平 α=0.05 进行比较：

• 由于 0.0104 < 0.05，我们拒绝零假设 \(H_{0}\)。

背景结论：在 5% 的水平上有统计显著的证据表明当前缺陷率超过了 7% 的历史水平。这表明制造过程可能正在经历质量下降，应调查纠正措施。

备注 14：尽管缺陷率从 7% 增加到 10% 可能看起来适中，但在高产量生产中可能具有重大的运营影响。例如，在一百万片微芯片的批次中，这种变化对应于额外的 30,000 个缺陷单元。这种变化可能需要立即调查过程质量、供应商绩效或机器校准

例2：

一位数字营销分析师正在评估新设计的电子商务登录页面的有效性。从历史上看，网站访问者的购买转化率约为 5%。推出重新设计后，分析师收集了 n=400 次网站访问的简单随机样本，观察到 x=30 位访问者完成了购买。

步骤 1：定义假设 设 p 为所有访问者中进行购买的真实比例。假设为： \(H_{0}: p=0.05\quad \text{（基线转化率）}\) \(H_{a}: p>0.05\quad \text{（由于新设计而增加）}\) 这是一个右尾检验，反映了检测改进的目标。

步骤 2：检查正态近似条件 我们验证应用 z 检验的大样本条件： \(n p_{0}=400 \cdot 0.05=20>5, \quad n\left(1-p_{0}\right)=400 \cdot 0.95=380>5\) 两个标准都满足，\(\hat{p}\) 的抽样分布可以用正态分布近似。

步骤 3：计算检验统计量 观察到的样本比例为： \(\hat{p}=\frac{30}{400}=0.075\)

检验统计量为： \(z=\frac{\hat{p}-p_{0}}{\sqrt{p_{0}\left(1-p_{0}\right) / n}}=\frac{0.075-0.05}{\sqrt{0.05 \cdot 0.95 / 400}} \approx \frac{0.025}{0.00883} \approx 2.83\)

步骤 4：计算 P 值 使用标准正态分布： \(P \text{-value} =\mathbb{P}(Z>2.83) \approx 0.0023\)

步骤 5：做出决策 在显著性水平 α=0.05 时：

• 由于 P 值 = 0.0023 < 0.05，我们拒绝零假设 \(H_{0}\)。

例3：

一家环境机构正在跟踪可持续消费者行为的变化，特别是可重复使用购物袋的使用情况。在之前的全国调查中，发现约 55% 的购物者在购物时定期携带可重复使用的袋子。在一个小型城市地区发起了一项新的外展活动，该机构希望评估这项工作是否导致了增长。在该地区随机调查了 n=80 名购物者，其中 x=50 人报告定期使用可重复使用的袋子。我们检验该比例是否超过了全国基准。

步骤 1：定义假设 设 p 表示该地区购物者中使用可重复使用袋子的真实比例。 \(H_{0}: p=0.55\quad \text{vs.}\quad H_{a}: p>0.55\)

步骤 2：检查 Z 检验条件 \(n p_{0}=80 \cdot 0.55=44>5, \quad n\left(1-p_{0}\right)=36>5\) 正态近似是合理的。

步骤 3：检验统计量和 P 值 \(\hat{p}=\frac{50}{80}=0.625, \quad z=\frac{0.625-0.55}{\sqrt{0.55(1-0.55) / 80}} \approx \frac{0.075}{0.0556} \approx 1.35\) \(P \text{-value} =\mathbb{P}(Z>1.35) \approx 0.0885\)

步骤 4：结论 由于 P 值 > 0.05，我们不拒绝 \(H_{0}\)。在 5% 的水平上，观察到的可重复使用袋子使用量的增加在统计上不显著。

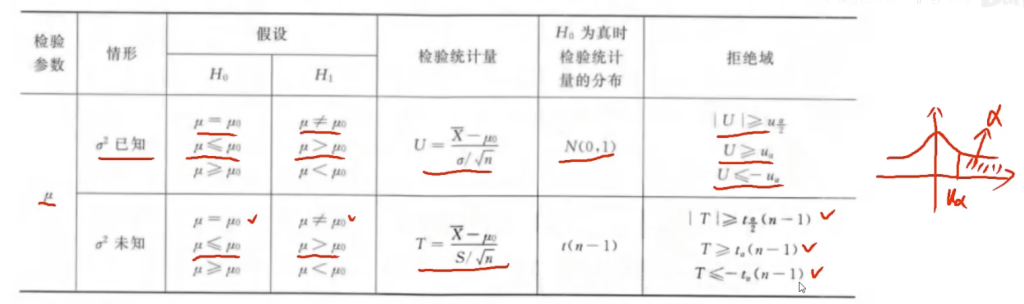
均值的检验统计量

• 均值的 Z 检验（当 σ 已知时）： \(z=\frac{\overline{x}-\mu_{0}}{\sigma / \sqrt{n}}\)
• 均值的 t 检验（当 σ 未知且使用样本标准差 s 时）： \(t=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}\)

使用 t 检验的情况：

• 总体近似正态，或
• 样本量足够大（n≥30），以便中心极限定理适用。

假设结构

我们检验：

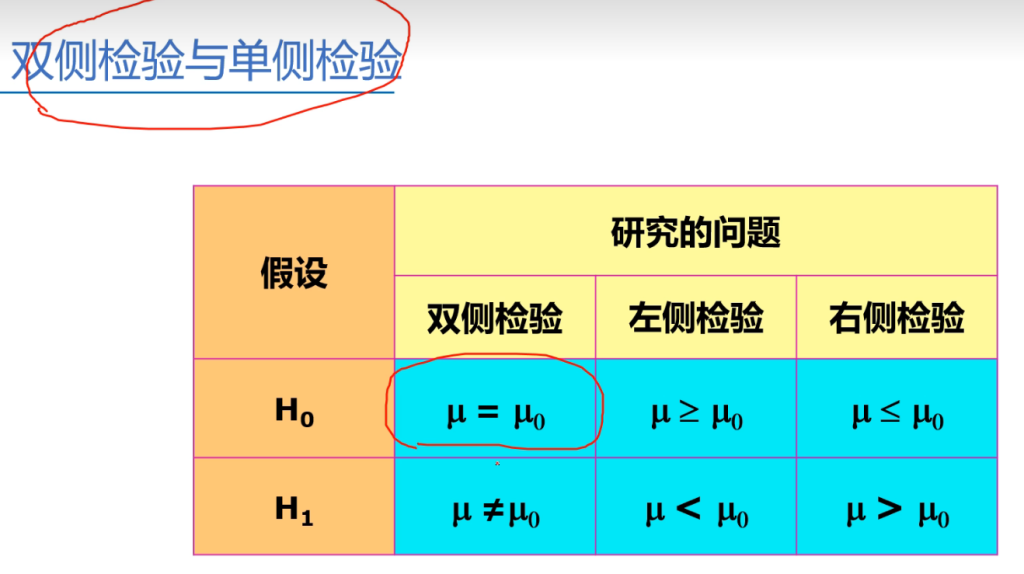
备择假设 \(H_{a}\) 的三种常见形式：

• 单侧上尾：\(H_{a}: \mu>\mu_{0}\)
• 单侧下尾：\(H_{a}: \mu<\mu_{0}\)
• 双侧：\(H_{a}: \mu \neq \mu_{0}\)

单侧检验的临界均值阈值

假设我们正在进行具有已知或估计标准误差和显著性水平 α 的单侧假设检验。

对于右尾检验 \(H_{a}: \mu>\mu_{0}\)，当以下情况时拒绝零假设： \(\overline{x}>\mu_{0}+z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}\quad \text{（Z检验）}\) \(\overline{x}>\mu_{0}+t_{\alpha, n-1} \cdot \frac{s}{\sqrt{n}}\quad \text{（t检验）}\)

同样，对于左尾检验 \(H_{a}: \mu<\mu_{0}\)，如果以下情况，我们拒绝 \(H_{0}\)： \(\overline{x}<\mu_{0}-z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}\quad \text{（Z检验）}\) \(\overline{x}<\mu_{0}-t_{\alpha, n-1} \cdot \frac{s}{\sqrt{n}}\quad \text{（t检验）}\)

双侧检验阈值

对于双尾检验 \(H_{a}: \mu \neq \mu_{0}\)，如果检验统计量落在中心 1−α 区域之外，我们拒绝零假设。这对应于： \(\left|\overline{x}-\mu_{0}\right|>z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}\quad \text{（Z检验）}\) \(\left|\overline{x}-\mu_{0}\right|>t_{\alpha / 2, n-1} \cdot \frac{s}{\sqrt{n}}\quad \text{（t检验）}\)

这也可以写成： \(\overline{x}<\mu_{0}-z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}} \quad \text{或} \quad \overline{x}>\mu_{0}+z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}\quad \text{（Z检验）}\) \(\overline{x}<\mu_{0}-t_{\alpha / 2, n-1} \cdot \frac{s}{\sqrt{n}} \quad \text{或} \quad \overline{x}>\mu_{0}+t_{\alpha / 2, n-1} \cdot \frac{s}{\sqrt{n}}\quad \text{（t检验）}\)

检验的功效（单侧备择假设）

为了评估检测真实均值 \(\mu=\mu_{1} \neq \mu_{0}\) 的功效，我们计算：

右尾（Z 检验）： \(1-\beta=\mathbb{P}\left(Z>\frac{\mu_{0}+z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}-\mu_{1}}{\sigma / \sqrt{n}}\right)=\mathbb{P}\left(Z>\frac{\mu_{0}-\mu_{1}+z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}}{\sigma / \sqrt{n}}\right)\)

右尾（t 检验）： \(1-\beta=\mathbb{P}\left(T_{n-1, \delta}>t_{\alpha, n-1}\right), \quad \delta=\frac{\mu_{1}-\mu_{0}}{s / \sqrt{n}}\)

这里，\(T_{n-1, \delta}\) 表示服从自由度为 n−1 且非中心参数为 δ 的非中心 t 分布的随机变量。与标准 t 分布（对称且以 0 为中心）不同，非中心 t 分布是不对称的，并根据 δ 的大小和方向移动。它用于在备择假设 \(\mu=\mu_{1}\) 下对检验统计量的抽样分布进行建模，从而在 σ 未知且使用 s 时实现精确的功效计算。

左尾（Z 检验）： \(1-\beta=\mathbb{P}\left(Z<\frac{\mu_{0}-z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}-\mu_{1}}{\sigma / \sqrt{n}}\right)=\mathbb{P}\left(Z<\frac{\mu_{0}-\mu_{1}-z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}}{\sigma / \sqrt{n}}\right)\)

左尾（t 检验）： \(1-\beta=\mathbb{P}\left(T_{n-1, \delta}<-t_{\alpha, n-1}\right)\)

双侧备择假设的检验功效

对于双侧情况 \(H_{a}: \mu \neq \mu_{0}\)， \(1-\beta=\mathbb{P}\left(T_{n-1, \delta}<-t_{\alpha / 2, n-1}\right)+\mathbb{P}\left(T_{n-1, \delta}>t_{\alpha / 2, n-1}\right), \quad \delta=\frac{\mu_{1}-\mu_{0}}{s / \sqrt{n}}\)

t 检验： \(1-\beta \approx \mathbb{P}\left(Z<\frac{\mu_{0}-z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}-\mu_{1}}{\sigma / \sqrt{n}}\right)+\mathbb{P}\left(Z>\frac{\mu_{0}+z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}-\mu_{1}}{\sigma / \sqrt{n}}\right)\)

Z 检验：

备注 18：对于小样本，使用自由度为 n−1 且非中心参数为 \(\delta=\frac{\mu_{1}-\mu_{0}}{s / \sqrt{n}}\) 的非中心 t 分布。对于大 n，基于正态近似的功效计算变得越来越准确。

例4：

城市发展当局担心日益严重的交通拥堵增加了居民的通勤时间。从历史上看，该市的平均通勤时间为 30 分钟。一位城市规划师希望确定这个平均值是否增加了。

为了调查，随机选择了 n=16 名居民的样本。该样本产生的平均通勤时间为 \(\bar{x}=32.4\) 分钟，样本标准差为 s=3.8 分钟。

步骤 1：定义假设 设 μ 表示所有城市居民的真实平均通勤时间。 \(H_{0}: \mu=30\quad \text{vs.}\quad H_{a}: \mu>30\) 这是一个右尾检验，适合检测平均通勤时间的增加。

步骤 2：假设

• 样本是从城市通勤者总体中随机抽取的。
• 样本量小（n=16），因此只有当通勤时间的分布近似正态时，t 检验才合适。
• 数据中没有报告重大异常值或强偏度。

步骤 3：检验统计量 我们使用单样本 t 检验公式： \(t=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{32.4-30}{3.8 / \sqrt{16}}=\frac{2.4}{0.95} \approx 2.526\)

自由度： \(d f=n-1=15\)

步骤 4：P 值方法 使用自由度为 15 的 t 分布： \(P \text{-value} =\mathbb{P}\left(T_{15}>2.526\right) \approx 0.012\)

决策：由于 P 值 = 0.012 < α=0.05，我们拒绝 \(H_{0}\)。

步骤 5：经典（临界值）方法 在 5% 显著性水平下，自由度为 15 的右尾 t 检验的临界值为： \(t_{0.05,15} \approx 1.753\) 由于 t=2.526 > 1.753，检验统计量落在拒绝域中。

结论：P 值和临界值方法都导致拒绝零假设。样本提供了统计显著的证据，表明平均通勤时间已超过 30 分钟的历史平均水平。

例5：

一家电信公司宣传客户通常等待不超过 10 分钟即可与代表通话。然而，最近的投诉引发了人们对平均等待时间可能与该标准不同的担忧。为了调查，一位主管选择了 n=25 个客户服务电话的简单随机样本。该样本产生的平均等待时间为 \(\bar{x}=9.4\) 分钟，样本标准差为 s=1.5 分钟。

我们旨在使用 α=0.05 显著性水平的双侧 t 检验，检验真实平均等待时间是否与广告中的 10 分钟不同。

假设： \(H_{0}: \mu=10\quad \text{vs.}\quad H_{a}: \mu \neq 10\)

检验统计量：由于总体标准差 σ 未知且样本量小（n<30），合适的检验是单样本 t 检验： \(t=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{9.4-10}{1.5 / \sqrt{25}}=\frac{-0.6}{0.3}=-2.0\)

自由度：\(d f=n-1=24\)

P 值方法：使用自由度为 24 的 t 分布： \(P \text{-value} =2 \cdot \mathbb{P}\left(T_{24}<-2.0\right) \approx 2 \cdot 0.029=0.058\)

结论：由于 P 值超过显著性水平（0.058 > 0.05），我们未能拒绝零假设。数据没有提供足够的统计证据来得出真实平均等待时间与 10 分钟不同的结论。

总结：错误、假设和程序

错误类型和功效

在假设检验中，三个关键概率决定了决策质量：

1. 第一类错误（α）：当 \(H_{0}\) 实际上为真时拒绝零假设的概率。例如，得出平均等待时间与 10 分钟不同的结论，而实际上并非如此。
2. 第二类错误（β）：当 \(H_{0}\) 为假时未能拒绝它的概率。这对应于忽略与声称的均值的真实偏差。
3. 功效（1−β）：正确拒绝错误零假设的概率。更高的功效表示检测真实效应的敏感性更高。

有效推断的假设

必须满足以下假设以确保推断程序的有效性：

• 样本必须是从总体中独立抽取的简单随机样本。
• 对于小样本（n<30），基础总体分布应近似正态。
• 对于大样本（n≥30），中心极限定理允许使用 t 或 z 检验，即使没有正态性。

五步假设检验程序

1. 陈述假设：清晰地制定零假设 \(H_{0}\) 和备择假设 \(H_{a}\)。
2. 检查假设：确定数据是否满足使用 z 检验或 t 检验的条件。
3. 计算检验统计量：使用适当的公式： \(z=\frac{\overline{x}-\mu_{0}}{\sigma / \sqrt{n}} \quad \text{或} \quad t=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}\)
4. 确定显著性：计算 P 值，或根据 α 将检验统计量与临界值进行比较。
5. 得出结论：根据证据决定是否拒绝 \(H_{0}\)，并在问题的背景下解释结果。

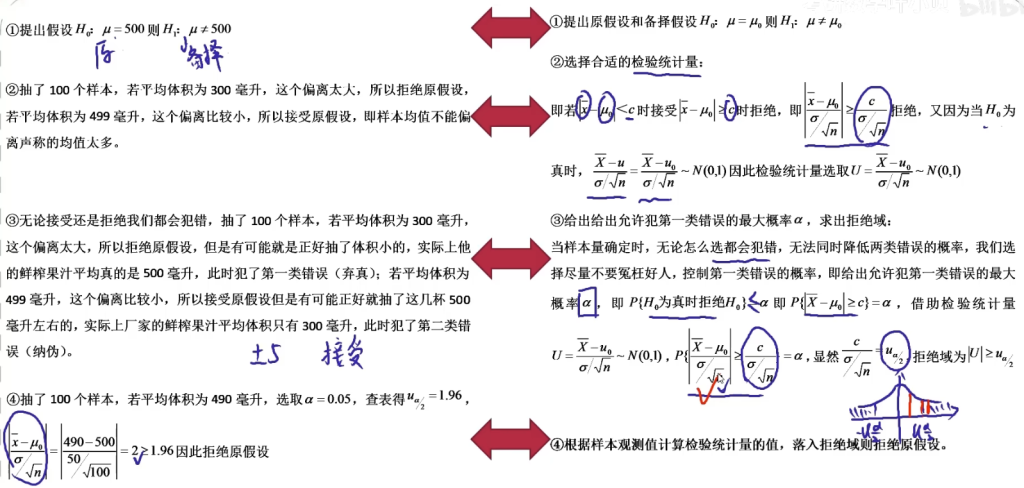
抽的样本均值和声称的均值差的大不大，如果很大，落入拒绝域(冤枉好人)，则拒绝原假设

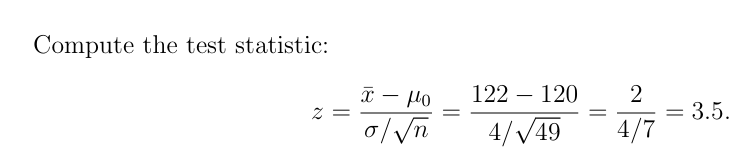
这步样本均值与原假设之间的差距大小，用标准差来衡量。z 值 = 3.5 表示：样本平均值比原假设的平均值大了 3.5 个标准差之多。

也就是说如果你画一条正态分布曲线：把右边最极端的 1% 留出来（也就是 0.01 的部分）那么这条边界线所在的 z 值就是 2.33，果你观察到的 z 值 超过了 2.33，那么就处于 非常罕见的右尾区域（只有 1% 的概率会落在那里）。如果你的 z 值大于 2.33，就说明你的观察结果太极端了，不太可能是巧合所以我们就会拒绝原假设

在原假设（null hypothesis）为真的前提下，观察到的统计量（或比它更极端的情况）出现的概率。