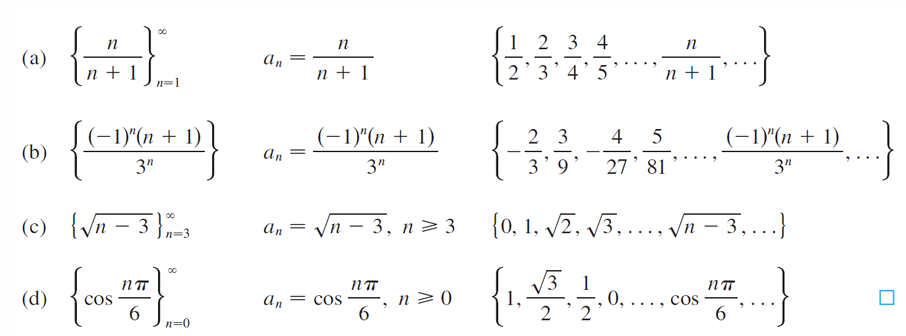二元函数

几何表达式求定义域

平面方程

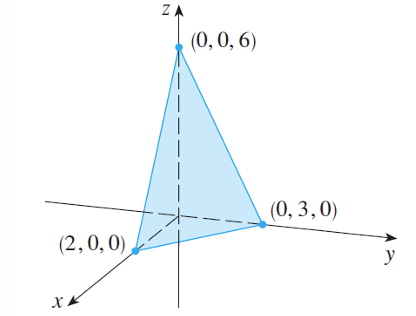
常见二次曲面方程(补充)

最高次数为2的三元方程

球体方程

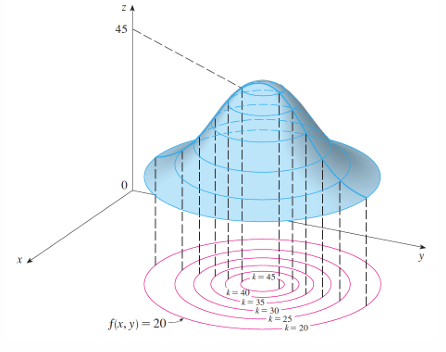
level Curves 等高线

二元函数 f 的等高线是方程 f(x,y)=k的曲线，其中 kk 为常数（属于 f的值域）。

等高线 f(x,y)=k 是定义域内所有使 f取值为 k的点的集合。换言之，它表示函数图像在高度 k 处的截面。

三元函数

level Surfaces 等值面

由于图像位于四维空间，三元函数 f的可视化非常困难。但通过观察其等值面(方程 f(x,y,z)=k的表面，k 为常数），我们可以获得一些理解。当点 (x,y,z)沿等值面移动时，函数值 f(x,y,z)保持不变

多元函数的极限

定义

做题思路：

即先尝试证极限不存在，如果发现无法证伪，在尝试证明极限存在

证明极限不存在

一元函数的极限，只有左/右逼近，二元及以上函数的极限可以从各个方向逼近，所以不能再用枚举法证明极限存在

例1：单路径法

降维成一元函数问题

例2：单路径法不能用于证明极限存在

如果\(f(x, y)=\frac{xy}{x^2 + y^2}\)，\(\lim_{(x, y)\rightarrow(0, 0)}f(x, y)\)是否存在？ 解：如果\(y = 0\)，那么\(f(x, 0)=\frac{0}{x^2}=0\)。因此，当\((x, y)\)沿着x轴趋近于\((0, 0)\)时，\(f(x, y)\rightarrow0\)。

如果\(x = 0\)，那么\(f(0, y)=\frac{0}{y^2}=0\)，所以当\((x, y)\)沿着y轴趋近于\((0, 0)\)时， \(f(x, y)\rightarrow0\)

尽管我们在坐标轴上得到了相同的极限，但这并不能说明所给极限就是0。现在让\((x, y)\)沿着另一条直线\(y = x\)趋近于\((0, 0)\)。对于所有\(x\neq0\)， \(f(x, x)=\frac{x^2}{x^2 + x^2}=\frac{1}{2}\)

所以当\((x, y)\)沿着\(y = x\)趋近于\((0, 0)\)时， \(f(x, y)\rightarrow\frac{1}{2}\)由于沿着不同路径得到了不同的极限，所以所给极限不存在

例3：y=kx^p路径法

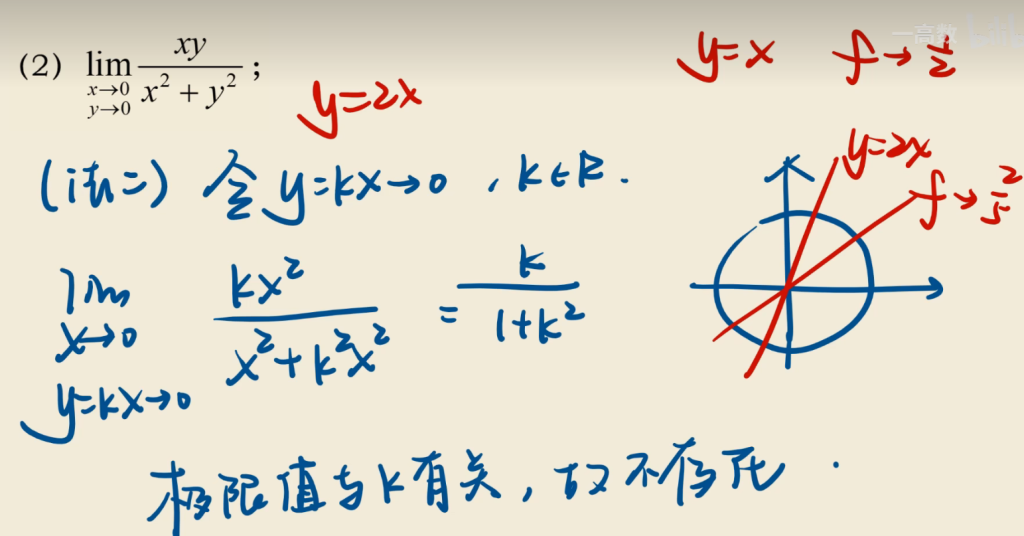
如果\(f(x, y)=\frac{xy^2}{x^2 + y^4}\)，当\((x, y)\)沿着过原点的任意非垂直直线趋近于\((0, 0)\)时，设\(y = mx\)（m为斜率），则 \(f(x, y)=f(x, mx)=\frac{x(mx)^2}{x^2+(mx)^4}=\frac{m^2x^3}{x^2 + m^4x^4}=\frac{m^2x}{1 + m^4x^2}\)

所以当\((x, y)\)沿着\(y = mx\)趋近于\((0, 0)\)时， \(f(x, y)\rightarrow0\)

因此，f在过原点的每一条非垂直直线上都有相同的极限值。但这并不能说明所给极限就是0，因为如果现在让\((x, y)\)沿着抛物线\(x = y^2\)趋近于\((0, 0)\)，则 \(f(x, y)=f(y^2, y)=\frac{y^2\cdot y^2}{(y^2)^2 + y^4}=\frac{y^4}{2y^4}=\frac{1}{2}\)

所以当\((x, y)\)沿着\(x = y^2\)趋近于\((0, 0)\)时， \(f(x, y)\rightarrow\frac{1}{2}\)

由于不同路径导致不同的极限值，所以所给极限不存在

如果存在极限

例1：连续点处直接代值

例2：无穷小代换求极限

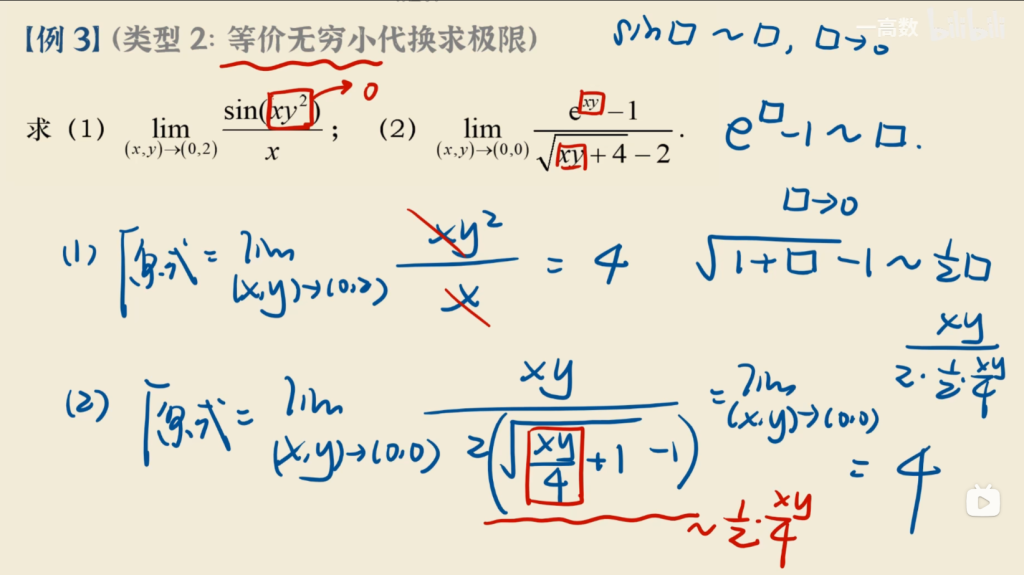
例3：无穷小量 × 有界值 -> 0

例4：夹逼定理 Squeeze theorem：套绝对值 ，就可以同时得到两侧的函数

此题也可在选择0 有限值的方法

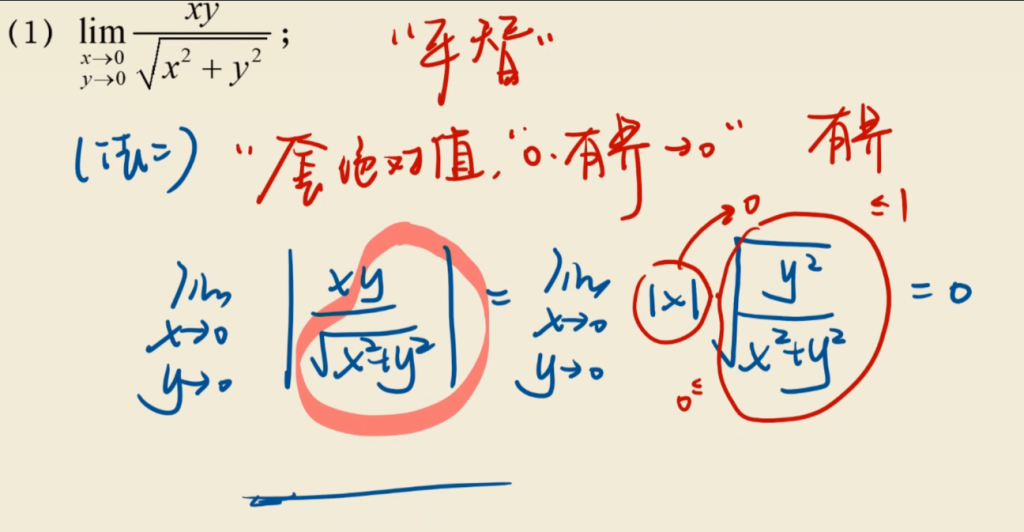
另一道夹逼的题：

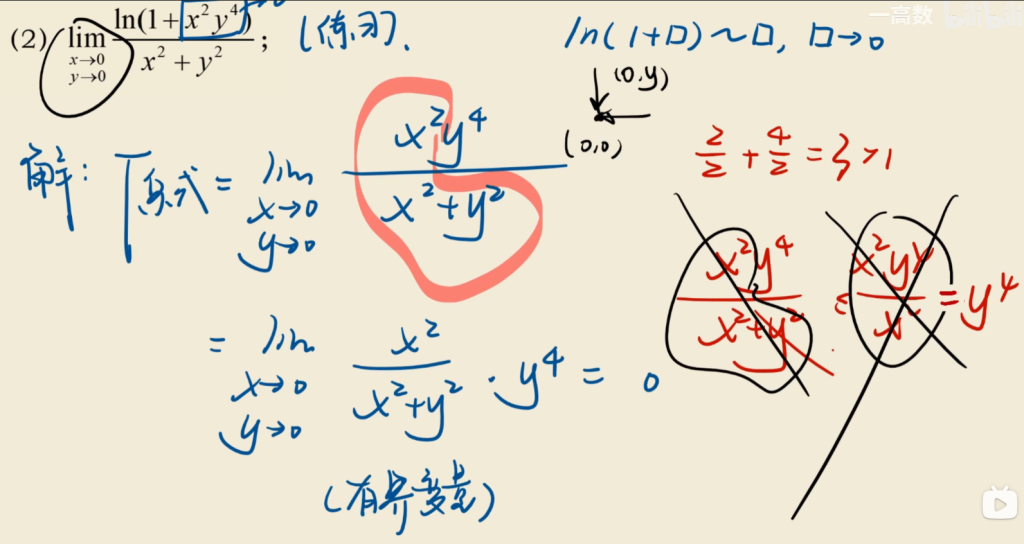
例5：等价无穷小 + 无穷小量 有限值

多元函数的连续性

定义

和一元相同，曲线某点连续的条件是极限与该点的函数值相同

解题思路

是否为一元初等函数的有限次四则 / 复合运算，如果点(a,b)是定义域的边界点(如分式分母等于0)，需额外定义f(a,b)的值，如果其值等于函数在(a,b)的极限则连续

例1：一元初等函数的有限次四则运算，在其定义域内都是连续的 – 多项式

计算\(\lim_{(x, y)\rightarrow(1, 2)}(x^2y^3 – x^3y^2 + 3x + 2y)\)。
解：由于\(f(x, y)=x^2y^3 – x^3y^2 + 3x + 2y\)是一个多项式，它在任何地方都连续，所以我们可以通过直接代入来求极限：
\(\lim_{(x, y)\rightarrow(1, 2)}(x^2y^3 – x^3y^2 + 3x + 2y)=1^2\cdot2^3 – 1^3\cdot2^2 + 3\cdot1 + 2\cdot2 = 11\)

例2：一元初等函数的有限次复合运算，在其定义域内都是连续的 – 有理函数

例3：无极值推得不连续

Vector Function 向量函数

定义域为一组实数，值域为一组向量的函数。我们最关注的是取值为三维向量的向量函数\(\mathbf{r}\)

• 这意味着对于\(\mathbf{r}\)定义域中的每一个数t，在三维向量空间\(V_3\)中都存在唯一的向量，记为\(\mathbf{r}(t)\)。
• 如果\(f(t)\)、\(g(t)\)和\(h(t)\)是向量\(\mathbf{r}(t)\)的分量，那么f、g和h是实值函数，称为\(\mathbf{r}\)的分量函数，我们可以写成： \(\mathbf{r}(t)=\langle f(t), g(t), h(t)\rangle = f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}\)

连续向量函数和空间曲线之间存在紧密联系，如果我们现在考虑向量函数\(\mathbf{r}(t)=\langle f(t), g(t), h(t)\rangle\)，那么\(\mathbf{r}(t)\)就是点\(P(f(t), g(t), h(t))\)在C上的位置向量。因此，任何连续向量函数\(\mathbf{r}\)都定义了一条空间曲线C，它由移动向量\(\mathbf{r}(t)\)的端点描绘出来

示例

描述由向量函数 \(\mathbf{r}(t)=\langle 1 + t, 2 + 5t, -1 + 6t\rangle\) 定义的曲线。 相应的参数方程为 \(x = 1 + t\quad y = 2 + 5t\quad z = -1 + 6t\) 这是一条过点\((1, 2, -1)\)且与向量\(\langle 1, 5, 6\rangle\)平行的直线的参数方程。或者，我们可以注意到该函数可以写成\(\mathbf{r}=\mathbf{r}_0 + t\mathbf{v}\)，其中\(\mathbf{r}_0=\langle 1, 2, -1\rangle\)，\(\mathbf{v}=\langle 1, 5, 6\rangle\)，这是直线的向量方程。

定义域

如果
\(\mathbf{r}(t)=\langle t^3,\ln(3 – t),\sqrt{t}\rangle\)
那么分量函数为
\(f(t)=t^3\quad g(t)=\ln(3 – t)\quad h(t)=\sqrt{t}\)
按照惯例，\(\mathbf{r}\)的定义域由所有使\(\mathbf{r}(t)\)表达式有意义的t值组成。表达式\(t^3\)、\(\ln(3 – t)\)和\(\sqrt{t}\)在\(3 – t > 0\)且\(t\geq0\)时均有意义。因此，\(\mathbf{r}\)的定义域是区间\([0, 3)\)。

极限

连续