发明初衷
泰勒级数是用多项式拟合一个函数,但用非周期函数去拟合一个周期函数,无法较好的体现周期函数的性质。因此使用最基本的周期函数即sin和cos去拟合周期为2Π(如果函数无周期或周期不是2Π的解决方案分别是展开和替换变量,见后)函数,因此引入三角级数又称傅里叶级数
公式
\(\cos(0\omega t)\)的结果是a0,为了形式的统一改写为 \(\frac{a_0}{2}\)
$$f(t) = \frac{a_0}{2} + a_1 \cos(\omega t) + b_1 \sin(\omega t) + a_2 \cos(2\omega t) + b_2 \sin(2\omega t) + \cdots$$$$ = \frac{a_0}{2} + \sum_{n=1}^{\infty} [a_n \cos(n\omega t) + b_n \sin(n\omega t)] $$
其中$$a_n = \frac{2}{T} \int_{t_0}^{t_0+T} f(t) \cos(n\omega t) \, dt $$$$ b_n = \frac{2}{T} \int_{t_0}^{t_0+T} f(t) \sin(n\omega t) \, dt $$
其中w为信号的频率,w = 2Π / T。后面都讨论T =2Π的情况,故w=1可省略不写。另外注意an的计算过程中分母为0时的n取值,要单独代入到原始式子求值(Exercise2 1.b)
在正交系统中,线性组合\[
\sum_{n=1}^{\infty} \langle f, e_n \rangle e_n
\]函数在基函数上的投影长度乘基函数的单位方向 – 原函数在基函数方向的分量,对这些分量求和即为原函数。而在三角函数系中的表示:\[
\frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right]
\]
注:上面使用了实值函数 \(\sin(nx)\) 和 \(\cos(nx)\) 作为正交系统,但也可以使用复值函数。在这种情况下,内积定义为:\[
\langle f, g \rangle = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) \overline{g(x)} \, dx
\]
复指数形式
$$f(x) = \sum_{n=-\infty}^{\infty} c_n e^{inx}$$$$c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) e^{-inx} \, dx, \quad n = 0, \pm 1, \pm 2, \ldots$$
证明(不用看)

同时\(\{1, e^{ix}, e^{-ix}, e^{i2x}, e^{-i2x}, \ldots\}\)也是一个正交系统
三角函数系及其正交性
三角函数系并不是一个坐标系,而是一个无限长的函数集合,进一步说,因为该函数集合满足闭包性,所以也是一个向量空间。
包含了常数函数1 以及所有频率为nω(n 为正整数)的正弦函数和余弦函数。这些函数在傅里叶分析中用作基函数,用于表示其他函数,作为函数空间中的基,可以将三角函数系类比为向量空间中的基向量:
- 在向量空间中,任何向量都可以表示为基向量的线性组合。
- 在函数空间中,任何函数都可以表示为三角函数系中函数的线性组合。
\[
\left\{
\frac{1}{\sqrt{2}}, \sin(x), \cos(x), \sin(2x), \cos(2x), \sin(3x), \cos(3x), \ldots
\right\}
\]
证明向量空间正交性
这里我们只展示其正交性,而不讨论其闭包性。通过函数的数量积证明函数之间正交\(\begin{align*}
\langle f, g \rangle = \int_a^b f(x) g(x) \, dx\end{align*}\)
(2)为0的原因是因为cos自变量相差的一个周期也可以从奇偶性的角度解释,345用积化和差证明

证明向量空间的归一性
定义范数:\[
\|f\| = +\sqrt{\langle f, f \rangle}
\]对于连续函数,可以很容易地证明:\[
\left\| \frac{1}{\sqrt{2}} \right\| = \frac{1}{\pi} \int_{-\pi}^{\pi} \frac{1}{2} \, dx = 1
\]类似地,对于每个 \( n = 1, 2, \ldots \),有:\[
\| \sin(nx) \| = \| \cos(nx) \| = 1
\]
推导an和bn

例题:

- 1.将需要转化的函数变成周期函数,再将展开的函数的定义域限制在(-Π,Π)中
- 2.套公式求出a0,an,bn。再套公式求出F(x)
- 3.可以发现拓展后的函数在nΠ的点处不连续
函数奇偶性简化 an 和 bn – 正余弦级数
如果 \( g \) 是奇函数,则对于任何 \( h > 0 \),有:\[
\int_{-h}^h g(x) \, dx = 0
\] 如果 \( g \) 是偶函数,则对于任何 \( h > 0 \),有:\[
\int_{-h}^h g(x) \, dx = 2 \int_0^h g(x) \, dx
\]
因此,偶函数的傅里叶级数只包含余弦项,奇函数的傅里叶级数只包含正弦项。
正弦级数和余弦级数是傅里叶级数的两种特殊形式,分别由正弦函数(sin)和余弦函数(cos)组成。它们通常用于表示奇函数或偶函数的傅里叶展开


狄利克雷收敛条件
狄利克雷收敛条件描述了在什么情况下,一个周期函数的傅里叶级数会收敛到该函数的原始值。换句话说,傅里叶级数可以准确地表示该函数(上题的等价改为等于的条件)
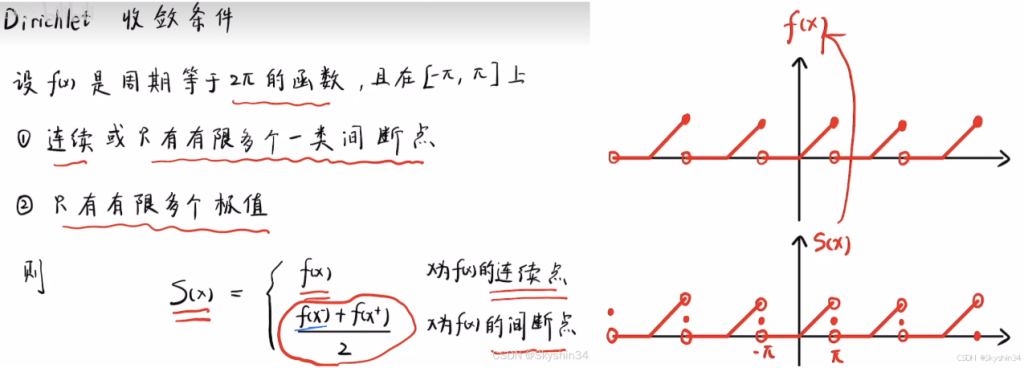
既然傅里叶级数展开的合函数在某些点不连续,没法拟合原来的值,所以只能取就取该点左极限和右极限各的一半即平均值。
周期为2L的函数如何展开
将周期为2L的原函数 f(x)通过变量代换变成一个新的周期为2Π的函数 F(t)

例题
Now suppose \( f(x) = |x| \) for \( x \in [-\pi, \pi] \) which is clearly an even function so we need to construct a cosine series with coefficients\[
a_0 = \frac{2}{\pi} \int_{0}^{\pi} x \, dx = \frac{2}{\pi} \frac{\pi^2}{2} = \pi
\]and for \( n = 1, 2, \ldots \)\[
a_n = \frac{2}{\pi} \int_{0}^{\pi} x \cos(nx) \, dx = \frac{2}{\pi} \left\{ \left[ \frac{x \sin(nx)}{n} \right]_0^{\pi} – \int_{0}^{\pi} \frac{\sin(nx)}{n} \, dx \right\}
\]\[
= \frac{2}{\pi} \left\{ \left[ \frac{\cos(nx)}{n^2} \right]_0^{\pi} \right\} = \frac{2}{\pi} \left\{ \frac{(-1)^n – 1}{n^2} \right\} =
\begin{cases}
\frac{4}{\pi n^2} & n \text{ is odd} \\
0 & n \text{ is even}
\end{cases}
\]Hence, the Fourier series of \( f(x) = |x| \) on \( x \in [-\pi, \pi] \) is\[
\frac{\pi}{2} – \sum_{k=1}^{\infty} \frac{4}{\pi (2k-1)^2} \cos((2k-1)x)
\]








