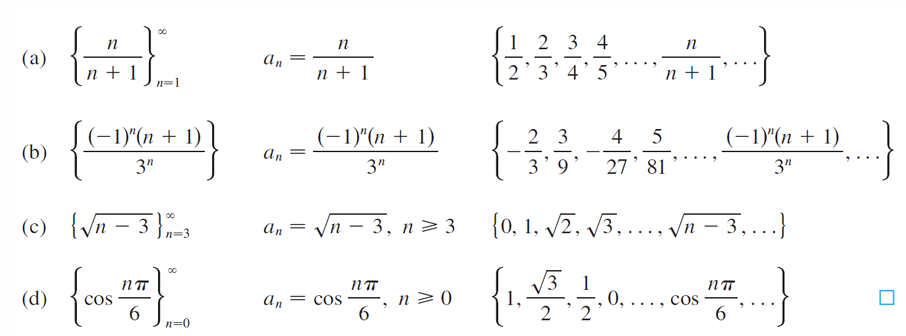scalars 标量(F) Linear space 线性空间(V)
也称为向量空间(Vector Space),满足两个运算加法和数乘以及八条公理:

标量域 F 的两种常见选择是实数 R 和复数 C,分别产生实线性空间和复线性空间。

Linear subspace
不同的变换可以看作是向特定向量空间的“投影”
投影的本质:降维或提取特定方向的信息。
在几何中,投影是指将一个向量映射到另一个向量或子空间上的过程。例如:
- 将向量 v 投影到向量 u 上,结果是 v在 u 方向上的分量。
- 将向量 v 投影到子空间 W 上,结果是 v 在 W 中的最近点。
变换与投影的类比
数学中的变换(如傅里叶变换、小波变换等)可以看作是将数据或函数从原始空间映射到另一个特定的向量空间中。这种映射过程类似于投影,因为:
- 提取特定特征:变换将数据分解为特定基函数的线性组合,提取出某些特征(如频率成分)。
- 降维:变换通常会将高维数据映射到低维空间,类似于投影将向量映射到子空间。
傅里叶变换Fourier transform将时域信号 f(t) 映射到频域空间,这里的频域空间是由正弦和余弦函数组成的向量空间,傅里叶变换可以看作是将信号“投影”到这个空间中,还有小波变换 wavelet transforms或任何其他线性变换。
投影到子空间有时称为降维。在三维空间中:任何通过原点的直线是一个一维子空间。任何通过原点的平面是一个二维子空间
Linear combinations 线性组合
给定一组向量 v1,v2,…,vk和一组标量 α1,α2,…,αk,它们的线性组合是指以下形式的向量(αi 是标量:实数或复数)
$$\alpha_1 \mathbf{v}_1 + \alpha_2 \mathbf{v}_2 + \cdots + \alpha_k \mathbf{v}_k$$
几何意义
- 线性组合表示向量空间中向量的加权和。
- 在几何上,线性组合可以看作是从原点出发,沿着各个向量方向按比例移动的结果。
根据本文后面提到的向量空间\(\{e_1, e_2, \ldots\}\) 的性质,还可以表示为 \(f \in E\):\[
\sum_{n=1}^{\infty} \langle f, e_n \rangle e_n
\]
- ⟨f,en⟩是函数 ff 在基函数 en上的投影系数。
- en 是正交基函数。
Spans 生成空间
给定一组向量 v1,v2,…,vk,它们的生成空间是指所有可能的线性组合构成的集合:
$$\text{Span}({v_1, v_2, \ldots, v_k}) = {\alpha_1 v_1 + \alpha_2 v_2 + \cdots + \alpha_k v_k \mid \alpha_i \in \mathbb{R}}.$$
生成空间是包含这组向量的最小线性子空间,是由一组向量的所有线性组合构成的集合,生成空间的维度取决于向量的线性无关性。
Linear independence 线性无关
如果一组向量是线性无关的,那么它们之间没有冗余,每个向量都不能表示为其他向量的线性组合。
给定一组向量 v1,v2,…,vk,如果满足以下条件,则称这组向量是线性无关的:
$$\alpha_1 v_1 + \alpha_2 v_2 + \cdots + \alpha_k v_k = 0$$
当且仅当所有标量 α1,α2,…,αkα1,α2,…,αk 都为零时成立。换句话说,唯一的线性组合使得结果为零向量的方式是所有系数都为零。
Bases 基
设 V是一个向量空间,B={v1,v2,…,vn} 是 V 中的一个向量组。如果满足以下两个条件,则 B 是 V 的一个基:
- 线性无关:
B 中的向量是线性无关的。 - 生成空间:
B 生成整个向量空间 V,即 V=Span(B)。
Inner products and inner product spaces 内积与内积空间
假设 V 是一个实或复线性空间(即标量 F=R 或 F=C),用⟨u,v⟩∈F 表示两个向量 u,v∈V的内积,是一个标量值,满足
- 对于每个 v∈V, ⟨v,v⟩≥0
- 对于每个 v∈V,⟨v,v⟩=0 当且仅当 \( v = \bar{0} \)
- 对于所有 u,v,w∈V和 a,b∈F,⟨au+bv,w⟩=a⟨u,w⟩+b⟨v,w⟩ 从投影的角度理解会很容易
- 对于所有 u,v∈V,\(\langle u, v \rangle = \overline{\langle v, u \rangle}\)
这里,\(\langle u, v \rangle = \overline{\langle v, u \rangle}\)表示复数 ⟨v,u⟩的复共轭。注意,对于实线性空间(即 F=R),复共轭是多余的,因此上述第四个条件仅表示 ⟨u,v⟩=⟨v,u⟩。但对于复向量,内积的顺序很重要。
内积的性质
共轭对称性:交换律 ⟨x,y⟩=⟨y,x⟩在实数向量空间中是成立的,因为实数的共轭就是其本身,所以内积的结果与向量的顺序无关。更通用的情况$$\langle \vec{x}, \vec{y} \rangle = \overline{\langle \vec{y}, \vec{x} \rangle}$$共轭的原因确保了内积的正定性。对于复数向量 \(\vec{v}\),内积 \(\langle \vec{v}, \vec{v} \rangle\) 必须是一个非负实数。如果直接使用交换律而不考虑共轭,可能会导致内积结果不是实数
例题:\(\vec{x} = (1 + i, 2 – i), \quad \vec{y} = (3 – 2i, 4 + i)\)内积定义为:\(\langle \vec{x}, \vec{y} \rangle = x_1 \overline{y_1} + x_2 \overline{y_2}\)其中 \(\overline{y_1}\) 和 \(\overline{y_2}\) 是 \(y_1\) 和 \(y_2\) 的复共轭。计算 \(\langle \vec{x}, \vec{y} \rangle\):
\(
\langle \vec{x}, \vec{y} \rangle = (1 + i)\overline{(3 – 2i)} + (2 – i)\overline{(4 + i)}
\)= (1 + i)(3 + 2i) + (2 – i)(4 – i) =8−i
线性性:
1. 在第一个变量上的线性性:\(\langle au + bv, w \rangle = a \langle u, w \rangle + b \langle v, w \rangle
\)这里 \(a\) 和 \(b\) 是标量(实数或复数)。
2. 在第二个变量上的共轭线性性(对于复数向量空间):\(\langle w, au + bv \rangle = \bar{a} \langle w, u \rangle + \bar{b} \langle w, v \rangle\)
$$\begin{align*}
\langle av, av \rangle = a \overline{a} \langle v, v \rangle = |a|^2 \langle v, v \rangle
\end{align*}$$
正定性:\(\langle f, f \rangle \geq 0\)且 \(\langle f, f \rangle = 0\) 当且仅当 \(f(x) = 0\) 几乎处处成立。
在实数域中,\(|a|^{2}=a^{2}\)。在复数域中,\(|a|^{2}=a^{2}\) 一般不成立。复数的模\(\vert a\vert\)的计算公式为\(\vert a\vert=\sqrt{x^{2}+y^{2}}\)例如,当\(a = 1 + i\)时,\(\vert a\vert^{2}=\sqrt{1^{2}+1^{2}}^2 = 2\) ,而\(a^{2}=(1 + i)^2=1 + 2i + i^2=2i\) ,此时\(\vert a\vert^{2}\neq a^{2}\)。
不同内积空间下的内积公式
定义:带有内积的线性空间
- 示例1(欧几里得空间,\(V = {R}^n\) ):给定两个向量 x=(x1,x2,…,xn)和 y=(y1,y2,…,yn),这里x1,x2…代表x向量在n维空间中的坐标分量,比如x=(3,4),x轴坐标分量为3,y轴坐标分量为4,在 Rn 中定义内积:
$$\langle x, y \rangle = \sum_{i=1}^n x_i y_i.$$ 通常,这个内积被称为点积,记作 x⋅y。
- 示例2(复向量空间,\(V = {C}^n\):类似地,我们可以通过以下方式定义内积:
$$\langle x, y \rangle = x \cdot y = \sum_{i=1}^n x_i \overline{y_i}$$
复平面向量内积运算中对分量取共轭是为了保证范数的非负性,向量的范数(长度)定义为 \(\|\mathbf{u}\| = \sqrt{\langle \mathbf{u}, \mathbf{u} \rangle}\)。若直接按实数内积逻辑(不共轭),复向量内积 \(\langle \mathbf{u}, \mathbf{u} \rangle = \sum_{i = 1}^{n} u_{i}^{2}\) 可能得到复数,无法定义合理的 “长度”。
- 示例3(区间上的连续函数空间)C[a,b]这里的 C 是 连续(Continuous)的缩写,表示定义在闭区间 [a,b]上的所有连续函数的集合。V=C[a,b]表示将这个函数空间赋予一个特定的结构(通常是线性空间或内积空间)通过以下方式为 f,g∈C[a,b] 定义内积:
$$\langle f, g \rangle = \int_a^b f(x)g(x)dx$$
为什么是积分:现在“向量”已经变成了连续函数。这种推广可以被视为向量元素数量无限增加。之前的内积公式中,向量元素对应乘积的离散求和,在这种极限下,变成了两个函数乘积的连续积分。
在区间 \([-\pi, \pi]\) 上,三角函数(如 sin(nx) 和 cos(nx))的内积定义为:\[
\langle f, g \rangle = \int_{-\pi}^{\pi} f(x)g(x) \, dx.
\]如果直接使用这个定义,sin(nx) 和 cos(nx) 的范数会是 \(\sqrt{\pi}\),而不是 1。
\[
\| \sin(nx) \| = \sqrt{\int_{-\pi}^{\pi} \sin^2(nx) \, dx} = \sqrt{\pi}.
\]为了使得这些函数的范数为 1,通常会在内积定义中加入归一化系数 \(\frac{1}{\pi}\):\[
\langle f, g \rangle = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)g(x) \, dx.
\]\[
\| \sin(nx) \| = \sqrt{\frac{1}{\pi} \int_{-\pi}^{\pi} \sin^2(nx) \, dx} = 1.
\]这样,sin(nx) 和 cos(nx) 的范数就是 1,方便计算和使用。
数量积几何意义:相似性与正交性
- 类比向量内积:在向量空间中,内积 ⟨u,v⟩可以衡量两个向量的“相似性”。若内积为 正,表示两向量方向相近;若为 负,方向相反;若为 零,则向量正交(垂直)。
- 函数内积的推广:
对函数 f和 g,内积 ⟨f,g⟩ 通过积分(而非点积)衡量它们在区间 [−π,π]上的“整体相似性”。若 ⟨f,g⟩=0,称 f和 g 正交(例如,不同频率的正弦函数),图像表现为完全不会重合,与坐标轴围成面积相抵消。所以内积的绝对值越大,表示两函数在区间上的“重叠程度”越高。

数量积几何意义:正交投影与函数分解
- 投影意义:在向量空间中,内积可用于将向量投影到基向量上。类似地,在函数空间中,内积可将函数分解为 正交基函数 的线性组合。例如,傅里叶级数将周期函数分解为正交的正弦/余弦函数(或复指数函数)的叠加:\[ f(x) = \sum_n \langle f, e^{inx} \rangle \cdot e^{inx} \]其中系数 \(\langle f, e^{inx} \rangle\) 通过内积计算,表示函数在基函数方向上的“投影强度”。
Norms 范数
用于衡量向量、矩阵或函数的大小或长度的函数,因为其本身是由模长推广而来的,要推广一个概念有以下步骤

范数可以对应到任意线性空间中,模长是一个映射,其将n维的向量映射为一个实数\(\| \cdot \| : \mathbb{C}^n \rightarrow \mathbb{R}\)还有以下性质


设特征空间 \(\Omega\) 是 \(n\) 维实数向量空间 \(\mathbb{R}^n\), \(\mathbf{x}_i, \mathbf{x}_j \in \mathcal{X}\),
\(\mathbf{x}_i = \left( x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(n)} \right)^T\),
\(\mathbf{x}_j = \left( x_j^{(1)}, x_j^{(2)}, \cdots, x_j^{(n)} \right)^T\).
1. 闵可夫斯基距离(Minkowski distance, \(L_p\) 距离)
\(\mathbf{x}_i, \mathbf{x}_j\) 的 \(L_p\) 距离定义为:
\[
L_p (\mathbf{x}_i, \mathbf{x}_j) = \left( \sum_{l=1}^n \left| x_i^{(l)} – x_j^{(l)} \right|^p \right)^{\frac{1}{p}}
\]其中,\(p \geq 1\).
2. 曼哈顿距离(Manhattan distance)
当 \(p = 1\) 时,\(L_p\) 距离就变成了曼哈顿距离,定义为所有属性下的绝对距离之和:
\[
L_1 (\mathbf{x}_i, \mathbf{x}_j) = \sum_{l=1}^n \left| x_i^{(l)} – x_j^{(l)} \right|
\]
3. 欧式距离(Euclidean distance)定义为所有属性下的平方距离之和的非负平方根
当 \(p = 2\), \(L_p\) 距离就变成了欧几里得距离,也就是常见的距离公式:
\[
L_2 (\mathbf{x}_i, \mathbf{x}_j) = \left( \sum_{l=1}^n \left| x_i^{(l)} – x_j^{(l)} \right|^2 \right)^{\frac{1}{2}}
\]
4. 切比雪夫距离(Chebyshev distance)
当 \(p \to \infty\), \(L_p\) 距离就变成了切比雪夫距离,两点之间各个坐标绝对距离的最大值:
\[
L_\infty (\mathbf{x}_i, \mathbf{x}_j) = \max_l \left| x_i^{(l)} – x_j^{(l)} \right|
\]
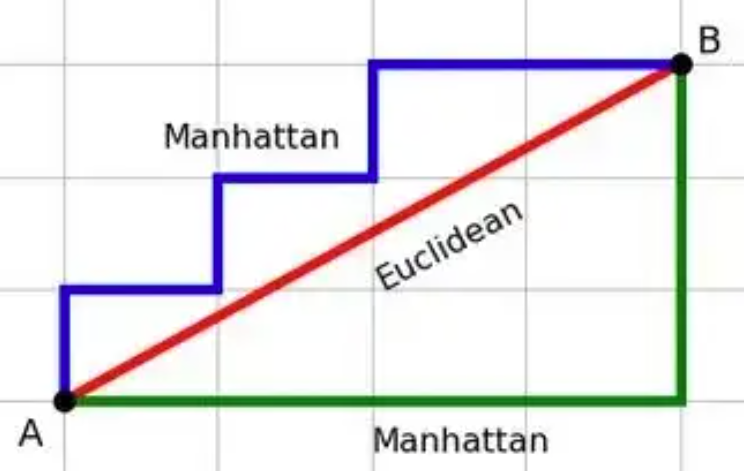
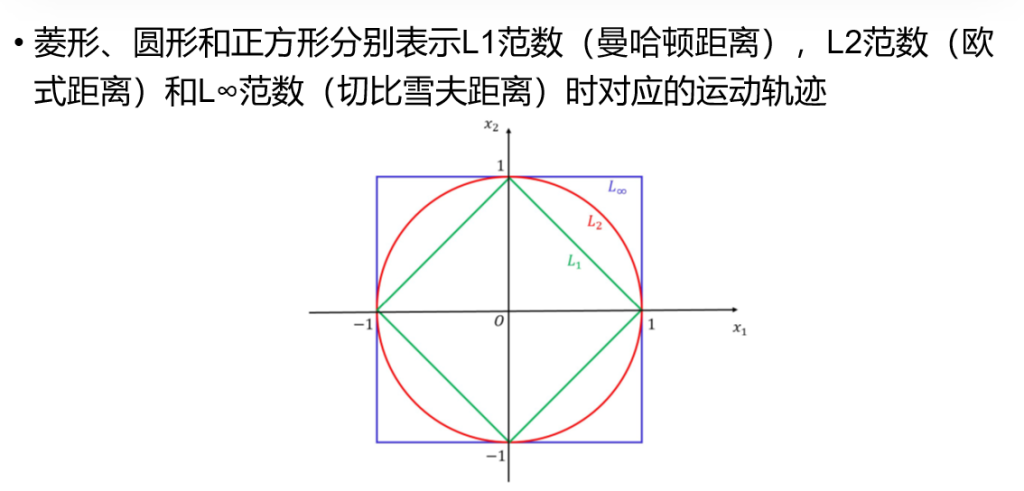
- L1范数(曼哈顿距离)满足 ∣x1∣+∣x2∣=1 的点构成菱形,顶点在坐标轴上(如 (1,0)(1,0)等)
- L2范数(欧式距离)满足 x12+x22=1x12+x22=1 的点构成单位圆
- L∞范数(切比雪夫距离)满足 max(∣x1∣,∣x2∣)=1的点构成边长为2的正方形,顶点在 (±1,±1)
Orthogonal and orthonormal systems 正交与正交归一系统
- 正交性:u,v∈V是正交的,记作 u⊥v,如果 ⟨u,v⟩=0
- 正交系统:对于所有 i≠j,有\(u_i \perp u_j\)
- 正交归一系统:此外,对于所有这样的向量 \(u_i\),有 \(| u_i |\)=1
使用特殊符号 \((e_i)\) 来表示构成正交归一系统的单位向量 \((u_i)\)


Infinite orthonormal systems 无限正交归一系统
由无限多个向量组成的正交归一系统。
Closure 闭包性
设 {u1,u2,…}是赋范线性空间 V 中的一个无限向量序列,{a1,a2,…}是某个标量序列。如果
$$\lim_{m \to \infty} \left\| w – \sum_{n=1}^m a_n u_n \right\| = 0.$$
无限正交归一系统 {un}{un} 的线性组合能够“生成”或“逼近”赋范线性空间 V 中的任意向量 w。如果一个向量空间中的向量在进行加法和标量乘法运算后,结果仍然属于该向量空间。则具有闭包性
例题
给定一个向量,求在正交系统中各分量的系数,套用以下公式即可



对于正交归一系统,快速计算向量积而不用再将其代入公式中

证明正交子集中的向量的内积可以简化为各分量系数的乘积与向量范数平方的和。