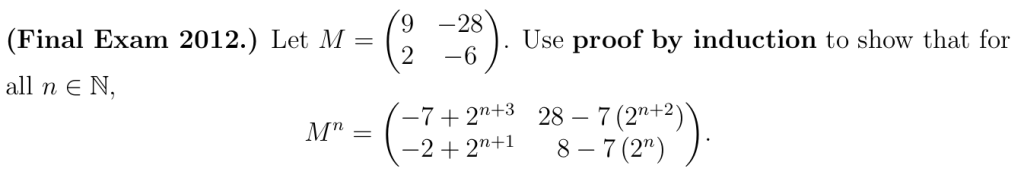马尔可夫链与马尔可夫过程

形式上，若系统在任意时刻的状态无法完全确定预测，但已知前一时刻状态时可预测当前状态的概率，则该变化过程称为马尔可夫链或马尔可夫过程。

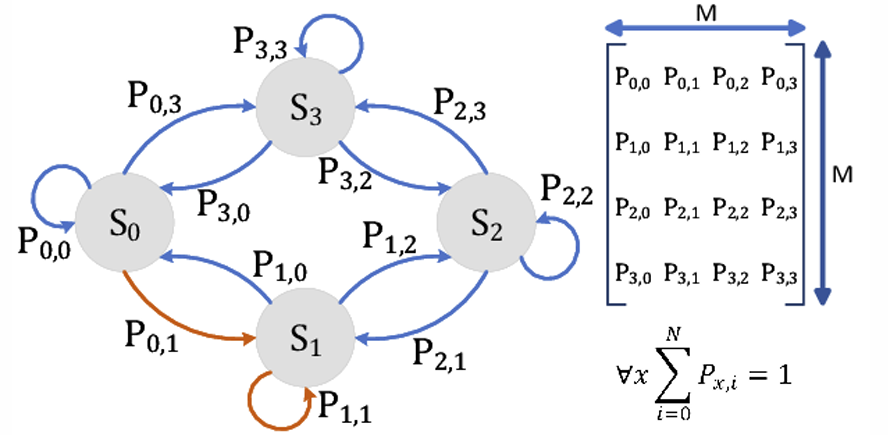
• 若马尔可夫链有k种可能状态（标记为\(1,2,\dots,k\)），则从状态j转移到状态i的概率记为\(p_{ij}\)，称为转移概率。
• 由转移概率构成的矩阵\(P = (p_{ij})\)称为转移矩阵。满足每行元素和为 1 的转移矩阵称为随机矩阵、概率矩阵或马尔可夫矩阵。

例：在一个小国中，有两家移动电话服务提供商：沃达丰（Vodafone）和橙子（Orange）。假设每年有 15% 的沃达丰用户转向橙子，而 20% 的橙子用户转向沃达丰。假定每年手机用户总数保持不变。我们需要为这类场景建立一个数学模型。

变量定义：我们需要表示橙子和沃达丰用户数量的变量，且不同年份的用户数需用独立变量表示。

• 设\(x_i\)为第i年沃达丰用户数，
• 设\(y_i\)为第i年橙子用户数。

从第i年到第\(i+1\)年，用户数的变化满足：\(x_{i+1} = 0.85x_i + 0.2y_i\)\(y_{i+1} = 0.15x_i + 0.8y_i\)

注意：相同变量系数的要放在同一列，否则与右侧乘出来的结果是错误的，代入进去很容易验证这一点。一定要验证矩阵和向量相乘的结果是否与方程组形式是否一致

向量矩阵方程：将用户数表示为向量\(\underline{x}(i) = \begin{pmatrix} x_i \\ y_i \end{pmatrix}\)，则状态转移可表示为：\(\begin{pmatrix} x_{i+1} \\ y_{i+1} \end{pmatrix} = \begin{pmatrix} 0.85 & 0.2 \\ 0.15 & 0.8 \end{pmatrix} \begin{pmatrix} x_i \\ y_i \end{pmatrix}\) 即\(\underline{x}(i+1) = M\underline{x}(i)\)，其中矩阵\(M = \begin{pmatrix} 0.85 & 0.2 \\ 0.15 & 0.8 \end{pmatrix}\)称为 “品牌转换矩阵”。

若考虑两年后的用户分布，则有：\(\underline{x}(i+2) = M\underline{x}(i+1) = M^2\underline{x}(i)\) 同理，n年后的用户分布为\(\underline{x}(i+n) = M^n\underline{x}(i)\)。这是一个 “马尔可夫链” 的例子，用户分布的长期行为由品牌转换矩阵M的幂次决定。

例2 – 犯了上面所说的错误，没有验证方程组与矩阵是否一致

In the town of Fibonacciville, there are two shops where people purchase their lunch, Sandeep’s Sandwiches and Dylan’s Delicatessen. Each citizen of Fibonacciville buys their lunch daily from one of the two lunch shops. From one day to the next, 21% of the people that previously bought their lunch at Sandeep’s Sandwiches switch to Dylan’s Delicatessen, while 34% of the people that previously bought their lunch at Dylan’s Delicatessen switch to Sandeep’s Sandwiches.

Express this situation in the form \(x(k + 1)=Mx(k)\), where M is a brand – switching matrix. Make sure that you state what your variables are and that you indicate the entries of M.

稳态向量Steady State Vectors

定义：矩阵A的稳态向量\(\underline{v}\)满足\(A\underline{v} = \underline{v}\)。 在品牌转换示例中，若\(\underline{x}(i)\)是矩阵M的稳态向量，则\(\underline{x}(i+1) = M\underline{x}(i) = \underline{x}(i)\)，即每年用户数保持不变（尽管用户仍在切换）。

验证示例：取稳态向量\(\underline{v} = \begin{pmatrix} 4 \\ 3 \end{pmatrix}\)，验证\(M\underline{v} = \underline{v}\)：\(M\underline{v} = \begin{pmatrix} 0.85 & 0.2 \\ 0.15 & 0.8 \end{pmatrix} \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 3.4 + 0.6 \\ 0.6 + 2.4 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \underline{v}\) 故\(\underline{v}\)是稳态向量。

关于稳态向量的标量倍数的定理：若\(\underline{v}\)是矩阵A的稳态向量，则其任意标量倍数\(k\underline{v}\)也是A的稳态向量。

然而，并非所有矩阵都有稳态向量。
例：矩阵\(A = \begin{pmatrix} 0.9 & 0.3 \\ 0.2 & 0.8 \end{pmatrix}\)没有稳态向量，但其存在一个特殊向量\(\underline{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix}\)。
计算\(A\underline{v}\)：\(A\underline{v} = \begin{pmatrix} 0.9 & 0.3 \\ 0.2 & 0.8 \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 2.7 + 0.6 \\ 0.6 + 1.6 \end{pmatrix} = \begin{pmatrix} 3.3 \\ 2.2 \end{pmatrix} = 1.1\begin{pmatrix} 3 \\ 2 \end{pmatrix} = 1.1\underline{v}\)
此时，\(A\underline{v}\)并非等于\(\underline{v}\)，但它是\(\underline{v}\)的标量倍数。

习题：求转换矩阵，根据转换矩阵预测，判断某向量是否为转换矩阵的稳态向量

特征值与特征向量 Eigenvalue Eigenvector

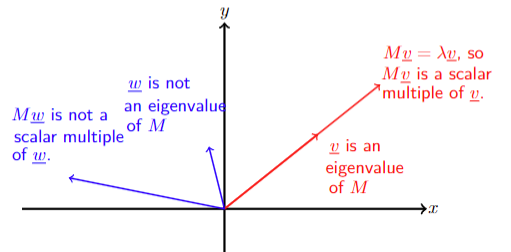
定义：对于方阵M，若存在非零向量\(v\)和标量\(\lambda\)，使得\(Mv = \lambda v\) 则称\(v\)为M的特征向量，\(\lambda\)为对应的特征值。

注：稳态向量是特征值\(\lambda = 1\)的特征向量。

几何意义（以\(\mathbb{R}^2\)为例）：

• 特征向量\(\underline{v}\)满足\(M\underline{v}\)是其自身的标量倍数，即向量方向不变（或反向），仅长度缩放。
• 非特征向量\(\underline{w}\)满足\(M\underline{w}\)不是其标量倍数，方向会发生改变。

关于特征向量的标量倍数的定理：若\(\underline{v}\)是矩阵M对应特征值\(\lambda\)的特征向量，则其任意标量倍数也是M对应同一特征值\(\lambda\)的特征向量。(上面是稳态向量的类似版本)

换句话说，一个特征值对应的特征向量不止一个，而是构成一个向量空间。在二维空间中（如 R2\mathbb{R}^2R2），一个特征值的所有特征向量组成一条通过原点的直线（一个一维子空间）。

虽然我们常用一个特征向量来表示，但实际上它的所有数倍与线性组合都是特征向量。

判断一个向量是否为矩阵的特征向量

如何求矩阵的特征向量和特征值？

特征方程，特征多项式

方程 \(\det(A – \lambda I) = 0\)（即 \(p(\lambda) = 0\)）称为矩阵 A 的 特征方程； 满足该方程的标量 \(\lambda\) 称为矩阵 A 的 特征值； 展开行列式 \(\det(A – \lambda I)\) 后得到关于 \(\lambda\) 的多项式 \(p(\lambda)\)，称为矩阵 A 的 特征多项式 Characteristic Polynomial。

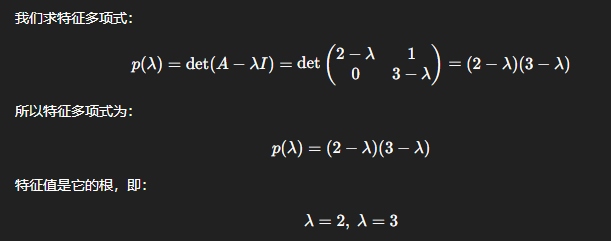
• 若 A 是 \(2 \times 2\) 矩阵，则 \(p(\lambda)\) 是 2 次多项式；
• 若 A 是 \(3 \times 3\) 矩阵，则 \(p(\lambda)\) 是 3 次多项式。

求特征值的方法：

解矩阵 A 的特征方程 \(\det(A – \lambda I) = 0\)，即可得到所有特征值

证明：
设 \(\underline{v}\) 是矩阵 M 对应特征值 \(\lambda\) 的特征向量，则\(M\underline{v} = \lambda\underline{v} = \lambda I\underline{v} \Rightarrow (M – \lambda I)\underline{v} = \underline{0}\)
这是一个关于 \(\underline{v}\) 分量的齐次线性方程组。
由于特征向量要求 \(\underline{v} \neq \underline{0}\)，因此该方程组需有非零解。
齐次方程组有非零解的充要条件是系数矩阵 \(M – \lambda I\) 不可逆，即 \(\det(M – \lambda I) = 0\)。

已知矩阵求特征值

求矩阵 \(M = \begin{pmatrix} -1 & 3 & 0 \\ 0 & 2 & 0 \\ -1 & 1 & 1 \end{pmatrix}\) 的所有特征值。
解：特征多项式为：\(\det(M – \lambda I) = \begin{vmatrix} -1 – \lambda & 3 & 0 \\ 0 & 2 – \lambda & 0 \\ -1 & 1 & 1 – \lambda \end{vmatrix}\)
按第一行展开：\(= (-1 – \lambda) \begin{vmatrix} 2 – \lambda & 0 \\ 1 & 1 – \lambda \end{vmatrix} – 3 \begin{vmatrix} 0 & 0 \\ -1 & 1 – \lambda \end{vmatrix}\)\(= (-1 – \lambda)(2 – \lambda)(1 – \lambda)\)
令行列式为零，解得：\(\lambda = -1, \, 2, \, 1\)
因此，矩阵 M 的特征值为 \(-1\)、2 和 1。

已知特征向量求特征值

如何求对应的特征向量？

对每个特征值 \(\lambda\)，解齐次线性方程组 \((A – \lambda I)\underline{v} = \underline{0}\)，其非零解即为对应特征向量。（注：若 \(\underline{v}\) 是特征向量，则其任意非零标量倍数也是特征向量，因此只需找出基础解系中的非零解。）

已知特征值求特征向量

设\(M = \begin{pmatrix}0.8&0.1\\0.2&0.9\end{pmatrix}\)为品牌转换矩阵，求其特征值与特征向量。 解： 1. 求特征值：\(\det(M – \lambda I) = (0.8 – \lambda)(0.9 – \lambda) – 0.02 = \lambda^2 – 1.7\lambda + 0.7 = 0\Rightarrow \lambda = 1, 0.7\) 2. 求特征向量： – 当\(\lambda_1 = 1\)时，解方程组\((M – I)\underline{v} = \underline{0}\)，得基础解系\(\underline{v}_1 = (1, 2)\)（稳态向量）； – 当\(\lambda_2 = 0.7\)时，解方程组\((M – 0.7I)\underline{v} = \underline{0}\)，得基础解系\(\underline{v}_2 = (-1, 1)\)

一种特殊情况：空间中的所有向量都可以作为某特征值的特征向量

每个向量\(\begin{pmatrix}x\\y\end{pmatrix}\in\mathbb{R}^2\)都是这个线性方程组的解，所以每个向量\(\begin{pmatrix}x\\y\end{pmatrix}\in\mathbb{R}^2\)都是矩阵\(A = \begin{pmatrix}a&0\\0&a\end{pmatrix}\)对应特征值\(\lambda = a\)的特征向量 。

我们该如何选取一个向量来表示所有特征向量呢？我们没法只用一个向量来代表所有特征向量。比如选取\(\underline{v}=\begin{pmatrix}1\\2\end{pmatrix}\)来表示所有特征向量（即\(\mathbb{R}^2\)中的所有向量 ），可\(\mathbb{R}^2\)里有很多向量不是\(\begin{pmatrix}1\\2\end{pmatrix}\)的标量倍数，所以\(\begin{pmatrix}1\\2\end{pmatrix}\)无法代表它们。每当我们试图用单个向量表示\(\mathbb{R}^2\)中所有向量时，都会碰到这个问题。由于\(\mathbb{R}^2\)是二维空间，我们需要两个向量来表示\(\mathbb{R}^2\)中的所有向量。这该如何操作呢？ 比如，我们可以选取\(\underline{i}=\begin{pmatrix}1\\0\end{pmatrix}\)和\(\underline{j}=\begin{pmatrix}0\\1\end{pmatrix}\)来表示对应特征值\(\lambda = a\)的所有特征向量 。此时，我们所认为的特征向量，不只是这些向量中某一个的标量倍数，实际上，是\(\underline{i}\)和\(\underline{j}\)的所有**线性组合**构成了对应特征值\(\lambda = a\)的特征向量。所谓“线性组合”，指的是所有形如\(\alpha\underline{i}+\beta\underline{j}\)的向量，其中\(\alpha,\beta\in\mathbb{R}\) 。所以，特征向量\(\underline{i}\)和\(\underline{j}\)代表了所有形如\(\alpha\underline{i}+\beta\underline{j}\)（\(\alpha,\beta\in\mathbb{R}\) ）的特征向量。且所有形如\(\alpha\underline{i}+\beta\underline{j}\)的向量都是矩阵\(A\)对应特征值\(\lambda = a\)的特征向量 。

综合习题

我们已学习如何计算任意方阵的特征值与特征向量。回顾品牌转换的例子：
每年沃达丰（Vodafone）有 15% 的客户流失至橙子（Orange），而橙子有 20% 的客户流失至沃达丰。设第i年沃达丰的客户数为xi​，橙子的客户数为yi​，则第i年的客户向量为x​(i)=(xi​yi​​)，后续年份的客户向量可通过品牌转换矩阵M与当前客户向量相乘得到

注意，如果初始值X的索引是1，要对n-1

Diagonal Matrices 对角矩阵

定义：方阵，除了主对角线（从左上到右下）上的元素外，其他元素全部为 0。

性质：

1. 行列式：对角矩阵的行列式等于主对角线元素的乘积。 例：\(\left| \begin{pmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -5 \end{pmatrix} \right| = 3 \times 1 \times (-5) = -15.\)
2. 幂运算：对角矩阵的幂等于主对角线元素各自取幂。 例：若\(D = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 3 \end{pmatrix}\)，则\(D^4 = \begin{pmatrix} 2^4 & 0 & 0 \\ 0 & 0^4 & 0 \\ 0 & 0 & 3^4 \end{pmatrix} = \begin{pmatrix} 16 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 81 \end{pmatrix}.\)
3. 可逆性：当且仅当主对角线元素全不为零时，对角矩阵可逆，且逆矩阵为对角线元素取倒数。 若\(D = \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{pmatrix}\)（\(a,b,c \neq 0\)），则\(D^{-1} = \begin{pmatrix} \frac{1}{a} & 0 & 0 \\ 0 & \frac{1}{b} & 0 \\ 0 & 0 & \frac{1}{c} \end{pmatrix}.\)

percentage不是算出来的，而是从矩阵中得到的

Similar Matrices 相似矩阵

定义：对于方阵 A 和 C，若存在可逆矩阵 B 使得\(C = B^{-1}AB\) 则称 C 与 A 相似。

性质

定理：设 C 与 A 相似，即 \(C = B^{-1}AB\)，则

• A 与 C 相似（因 \(A = (B^{-1})^{-1}C(B^{-1}) = BCB^{-1}\)）
• A 和 C 的行列式相等
• A 和 C 有相同的特征多项式 det(C−λI)=det(A−λI)，从而特征值相同
• \(\underline{v}\) 是 A 的特征向量当且仅当 \(B^{-1}\underline{v}\) 是 C 的特征向量

相似变换做了什么？当我们做C = \(B^-1\)AB这种变换时，其实我们只是把坐标系（基底）换了一下。矩阵 C和 A描述的是同一个线性变换，只是

C 是在“新基底”下的表示。A 是在“原始坐标系”里表示；

所以线性变换本质没变，只是换了坐标描述方式，于是：特征值（描述变换的本质）不会变！

但特征向量是方向，是在某个坐标系下的表示。换了基底后，在新基底下的方向会变成 \(B^−1\)v，这是坐标转换后的表示

其他的一些性质以及证明：

if A is similar to B and B is similar to C, then A is similar to C.

证明

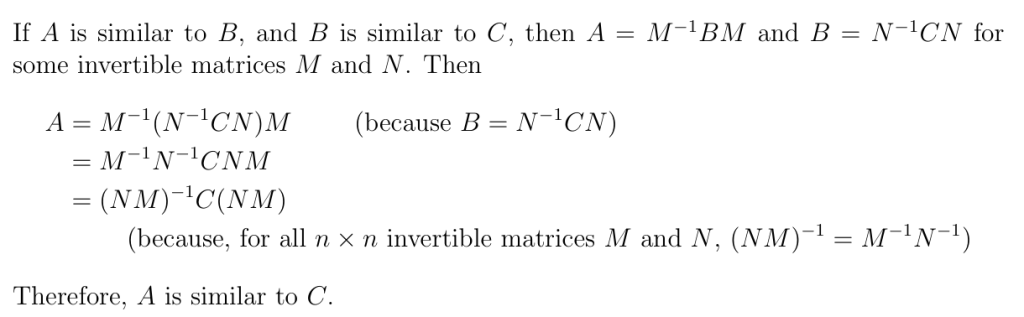
Let A be an invertible square matrix, and C be a square matrix that is similar to A.
C also invertible? If so, \(C^−1\) similar to \(A^−1\)

证明

Diagonalisation and powers of a Matrices 矩阵的对角化与幂运算

定义：若方阵 A 与对角矩阵 D 相似，即存在可逆矩阵 B 使得\(D = B^{-1}AB\) 则称 A 可对角化 diagonalisable matrix，D 称为 A 的标准形diagonal normal form

为什么可以这样分解，很简单，只需要对矩阵与其特征向量和特征值的关系式稍加移项即可得到

D是一个对角矩阵，对角线是 A的特征值；B是一个可逆矩阵，其列向量正是 A的一组线性无关特征向量；

定理：设 \(n \times n\) 矩阵 A 有特征值 \(\lambda_1, \lambda_2, \dots, \lambda_n\) 及对应的特征向量 \(\underline{v}_1, \underline{v}_2, \dots, \underline{v}_n\)。令 D 为对角元素为 \(\lambda_1, \lambda_2, \dots, \lambda_n\) 的对角矩阵，B 为以特征向量 \(\underline{v}_1, \underline{v}_2, \dots, \underline{v}_n\) 为列的矩阵，则\(D = B^{-1}AB\)

我犯过的错：

• D = B^-1 A B，中间的A是已知原矩阵，不要代错
• 矩阵计算是从右向左计算（这里其实不会错，因为3项可以利用结合律将左侧两个矩阵结合在一起）
• 矩阵相乘时最好写出式子，不要口算，我的平均错误率在2/9

对角化的应用：矩阵的幂

下面的例子可以对角化，求特征值，特征向量，代入求相似对角化的两个矩阵，然后再两边变换求幂公式，最后我列举了一个不能相似对角化的例子

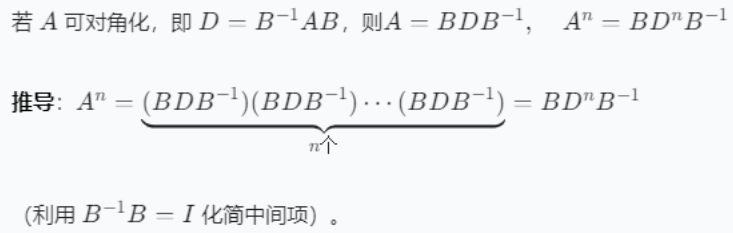
例2：

1. 本来不想放进来因为过程与上面的题目都右重合，但得到了5个实践巩固的收获：
2. 计算行列式，基础行变换如果将某行乘某个系数，最终行列式的结果也要乘这个数，其实并没有减少多少计算量。更常见的还是用在解方程组那里，不需要计算行列式，所以无所谓如何变换矩阵
3. 验证了特征值的顺序不影响相似对角化的最终表达式
4. 计算完逆矩阵一定要演算是否与原矩阵相乘等于1
5. 最重要的收获，上面一题用的是增广矩阵计算的逆矩阵，这次用代数余子式构成的伴随矩阵和矩阵的行列式计算矩阵的逆矩阵，意识到代数余子式不需要将忽略的项放进去，这里笔主将伴随矩阵使用代数余子式其与计算行列式时也使用代数余子式的方法混淆了

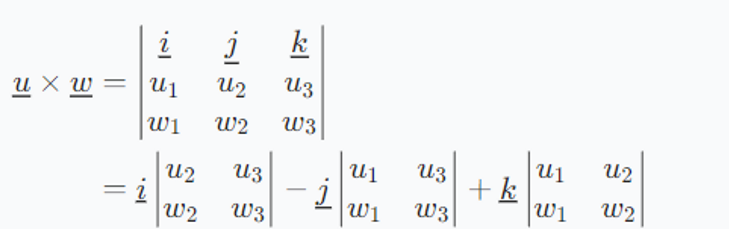
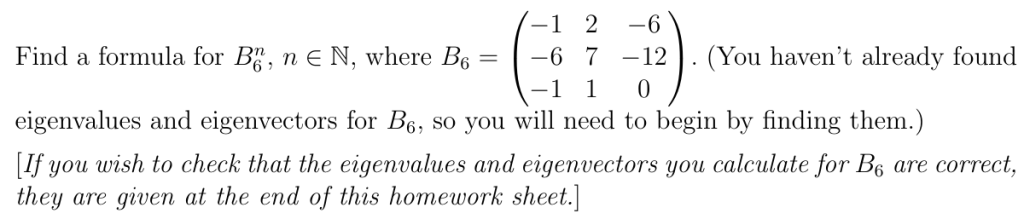
变式例题：未知矩阵，但已知矩阵的特征值和特征向量

其实就是按照上面的步骤求出A^n的式子，令n=1即可

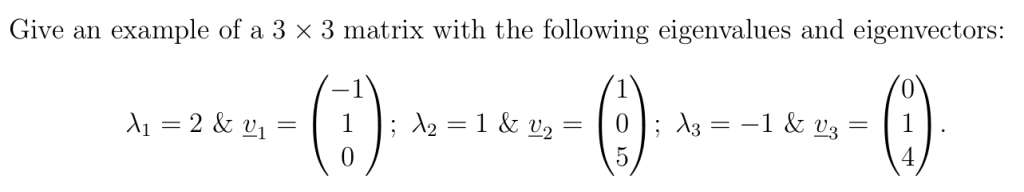
变式例题：交换特征值与特征向量的顺序

变式例题：使用特征向量的数乘

能否对角化的判断 – 特征向量数量不够

当一个n×n 矩阵拥有 n个互不相同的特征值时，它总是可对角化的。

（为了使一个矩阵可对角化，你需要能够从特征向量中构造出一个可逆矩阵。
如果你有 n个不同的特征值，这一点总是可以实现；但如果特征值少于 n个，那就只有在某些情况下才能实现。一个矩阵与它的转置总是具有相同的特征值，因此 A和 AT都拥有特征值，所以A^T 也是可对角化的。

证明

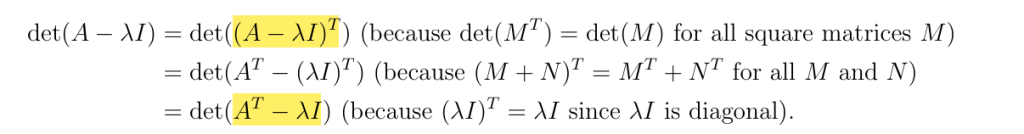
AT一定是A的相似矩阵，证明略

A是可对角化的，A^2也是可对角化矩阵，特征值变化规律

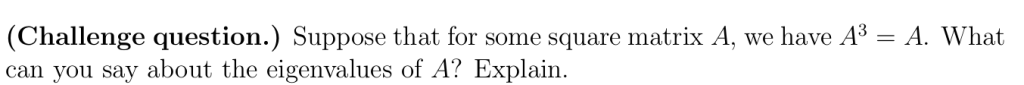
Proof by Induction 数学归纳法证明

回顾前两讲内容，我们通过对角化方法得到了方阵幂次的计算公式。现在将通过数学归纳法验证这些公式的正确性。
数学归纳法证明包含四个部分：基础情形、归纳假设、归纳步骤和结论。