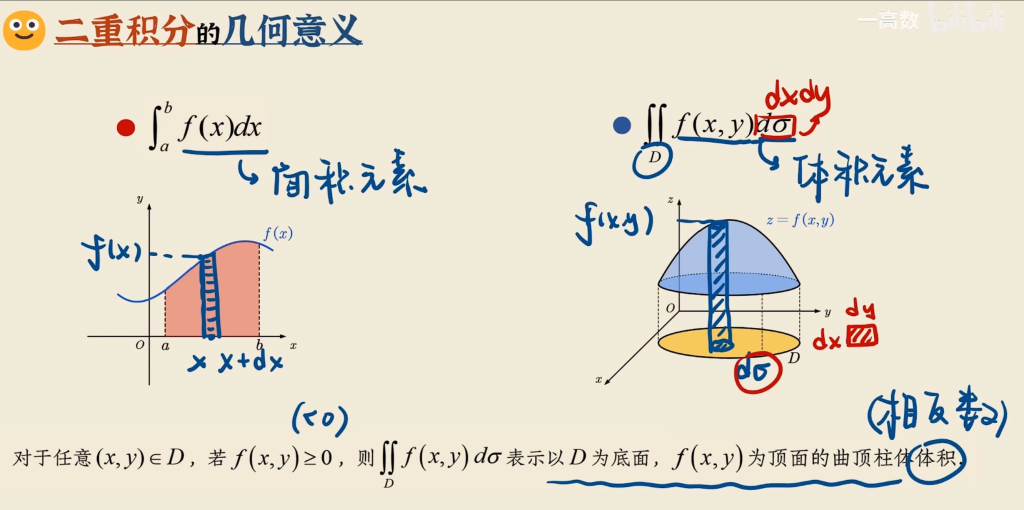
二重积分的几何意义

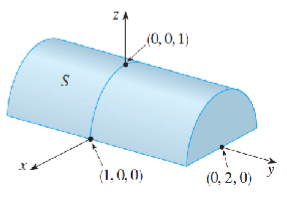
示例：若\(R = \{(x, y) \mid -1 \leq x \leq 1, -2 \leq y \leq 2\}\)，计算积分\(\iint_{R} \sqrt{1 – x^{2}} d A\) 由于\(\sqrt{1 – x^{2}} \geq 0\)，可将此积分理解为体积来计算。若\(z = \sqrt{1 – x^{2}}\)，则\(x^{2} + z^{2} = 1\)且\(z \geq 0\)，故给定的二重积分表示位于圆柱面\(x^{2} + z^{2} = 1\)下方、矩形R上方的立体S的体积。

S的体积为半径为 1 的半圆面积乘以圆柱的长度，因此 \(\iint_{R} \sqrt{1 – x^{2}} d A = \frac{1}{2} \pi (1)^{2} \times 4 = 2 \pi\)

如何画积分区域

抄积分范围

计算二重积分的步骤

The Midpoint Rule 中点规则

用于近似单变量积分的方，其中\(R_{ij}\)中的样本点\((x_{ij}^{*}, y_{ij}^{*})\)取为\(R_{ij}\)的中心\((\overline{x}_{i}, \overline{y}_{j})\)。换言之，\(\overline{x}_{i}\)是\([x_{i-1}, x_{i}]\)的中点，\(\overline{y}_{j}\)是\([y_{j-1}, y_{j}]\)的中点。

二重积分的性质

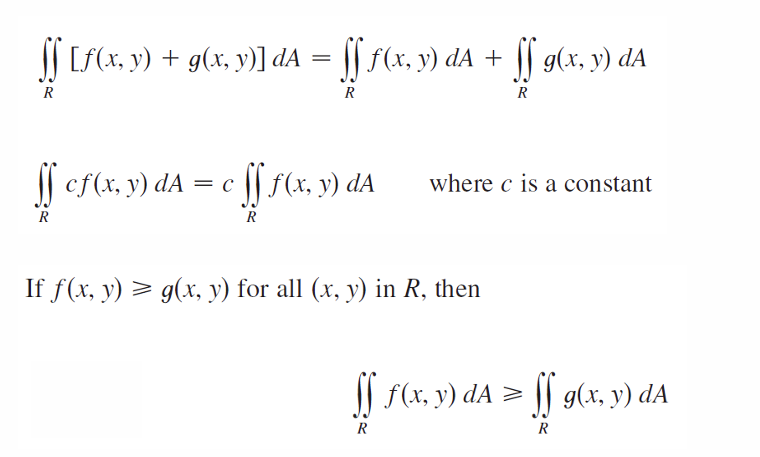
如果区域是“正常区域”且函数是连续的，积分顺序不会影响最终结果。

例题

例1 Evaluate \(\iint_{R} y sin (x y) d A\) ,where \(R=[1,2] \times[0, \pi]\)

第一步：把 y 提到外面（因为它与 x 无关）

\(=\int_{y = 0}^{\pi} y \left( \int_{x = 1}^{2} \sin(xy) \, dx \right) dy\) 注意对x积分，但sin内部是xy所以要换元

第二步：计算内层积分 \(\boldsymbol{\int_{x = 1}^{2} \sin(xy) \, dx}\)

令 \(u = xy\)，即对 x 积分时，把 y 当作常数。 换元：

• \(u = xy\)
• \(du = y \, dx \Rightarrow dx = \frac{du}{y}\)

当 \(x = 1 \Rightarrow u = y\) 当 \(x = 2 \Rightarrow u = 2y\)

所以： \(\int_{x = 1}^{2} \sin(xy) \, dx = \int_{u = y}^{2y} \sin(u) \cdot \frac{1}{y} du = \frac{1}{y} \int_{y}^{2y} \sin(u) \, du\) \(= \frac{1}{y} \big[ -\cos(u) \big]_{y}^{2y} = \frac{1}{y} \big( -\cos(2y) + \cos(y) \big)\)

第三步：代入外层积分

现在我们代入得到的结果： \(\int_{y = 0}^{\pi} y \cdot \frac{1}{y} \big( \cos(y) – \cos(2y) \big) dy = \int_{0}^{\pi} \big( \cos(y) – \cos(2y) \big) dy\)

第四步：分别积分

\(\int_{0}^{\pi} \cos(y) \, dy = \big[ \sin(y) \big]_{0}^{\pi} = \sin(\pi) – \sin(0) = 0\)

\(\int_{0}^{\pi} \cos(2y) \, dy = \left[ \frac{1}{2} \sin(2y) \right]_{0}^{\pi} = \frac{1}{2} \big( \sin(2\pi) – \sin(0) \big) = 0\)

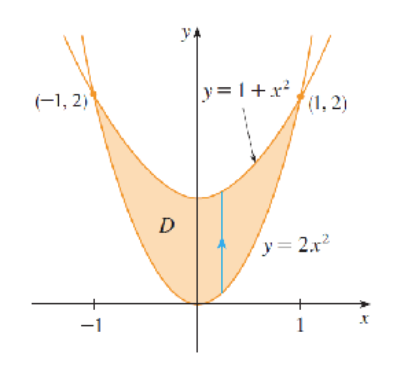
例2 Evaluate \(\iint_D (x + 2y) dA\), where D is the region bounded by the parabolas \(y = 2x^2\) and \(y = 1 + x^2\).

SOLUTION The parabolas intersect when \(2x^2 = 1 + x^2\), that is, \(x^2 = 1\), so \(x = \pm1\). We note that the region D, sketched in Figure 8, is a type I region but not a type II region and we can write

\(D = \left\{(x, y) \mid -1 \leqslant x \leqslant 1,\ 2x^2 \leqslant y \leqslant 1 + x^2\right\}\)

Since the lower boundary is \(y = 2x^2\) and the upper boundary is \(y = 1 + x^2\), gives

\(\begin{align*} \iint_D (x + 2y) dA &= \int_{-1}^{1} \int_{2x^2}^{1 + x^2} (x + 2y) dy\ dx \\ &= \int_{-1}^{1} \left[xy + y^2\right]_{y = 2x^2}^{y = 1 + x^2} dx \\ &= \int_{-1}^{1} \left[x(1 + x^2) + (1 + x^2)^2 – x(2x^2) – (2x^2)^2\right] dx \\ &= \int_{-1}^{1} \left(-3x^4 – x^3 + 2x^2 + x + 1\right) dx \\ &= \left. -3 \frac{x^5}{5} – \frac{x^4}{4} + 2 \frac{x^3}{3} + \frac{x^2}{2} + x \right]_{-1}^{1} = \frac{32}{15} \end{align*}\)