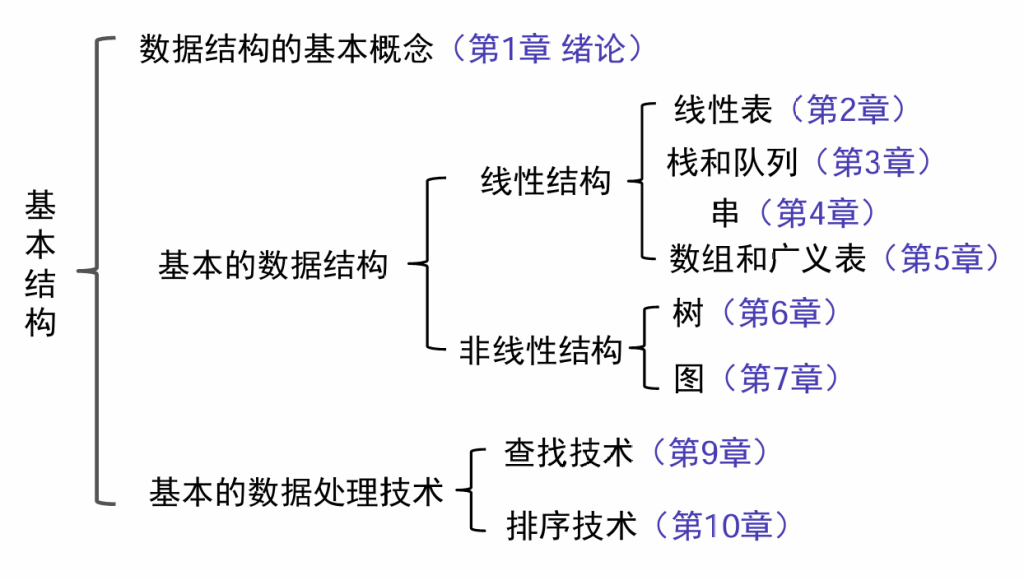
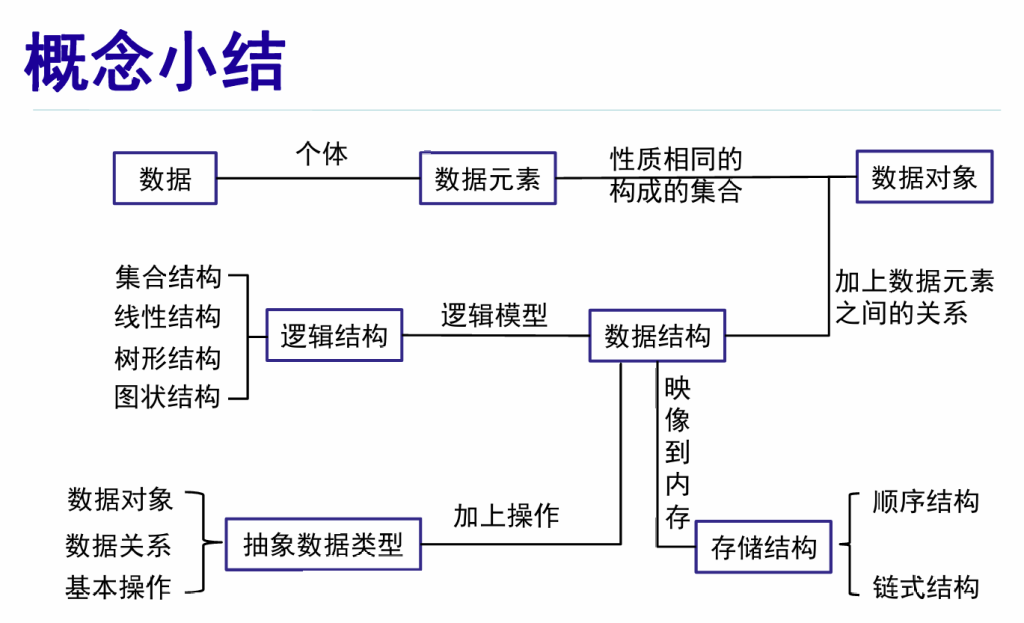
什么是数据结构

书目检索系统（线性表）计算机和人棋盘对弈问题（树）多叉路口交通灯管理问题（图），这些问题无法用数学的公式或方程来描述，是一些“非数值计算”的程序设计问题
描述非数值计算问题的数学模型不是数学方程，而是诸如表、树、图之类的具有逻辑关系的数据

定义：数据结构是一门研究非数值计算的程序设计中计算机的操作对象以及它们之间的关系和操作的学科

基本术语和概念

数据（data）

所有能输入到计算机中并能被计算机程序处理的符号的集合，包括：

• 数值型的数据：整数、实数等
• 非数值型数据：文字、图像、图形、声音等

数据元素（data element）

数据的基本单位
一个数据元素可由若干个数据项(data item)组成，
数据项是数据的最小单位

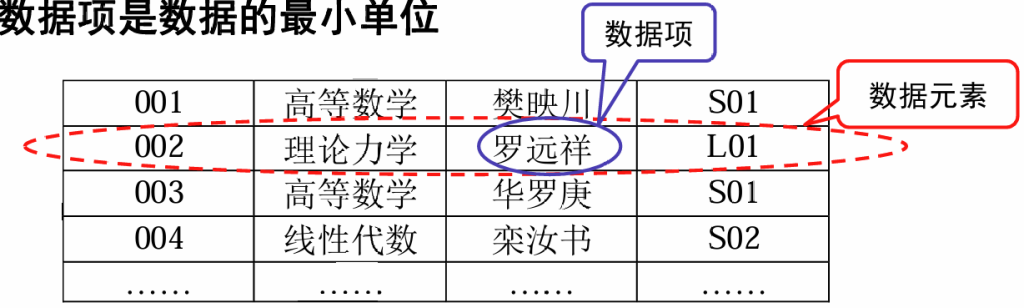
数据对象（data object）

是具有相同性质的数据元素的集合，是数据的一个子集
例如: 整数数据对象是集合N={0, ±1, ±2，…} 字母字符数据对象是集合C={‘A’，‘B’,…,‘Z’}

数据结构（data structure）

是相互之间存在一种或多种特定关系的数据元素的集合
数据元素之间的关系称为结构
从集合论的观点加以描述：数据结构是一个二元组：Data_Structure=(D, S)
D：数据元素的有限集 S：是D上关系的有限集

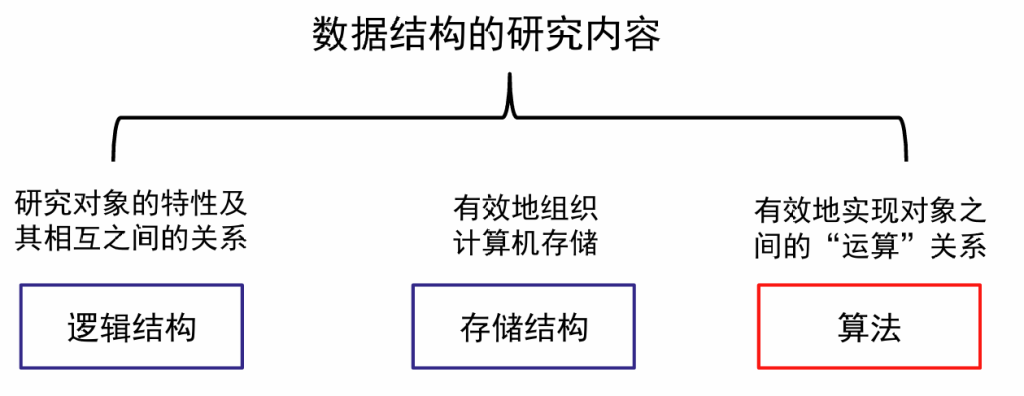
数据结构包括以下三个方面的内容：

• 逻辑结构：描述数据元素之间的逻辑关系

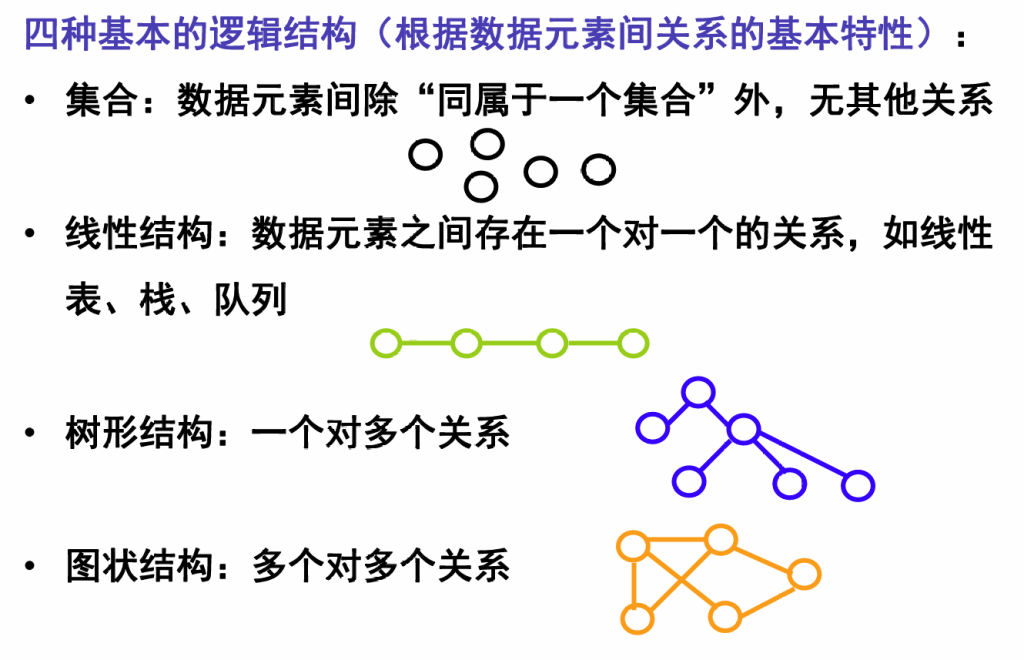
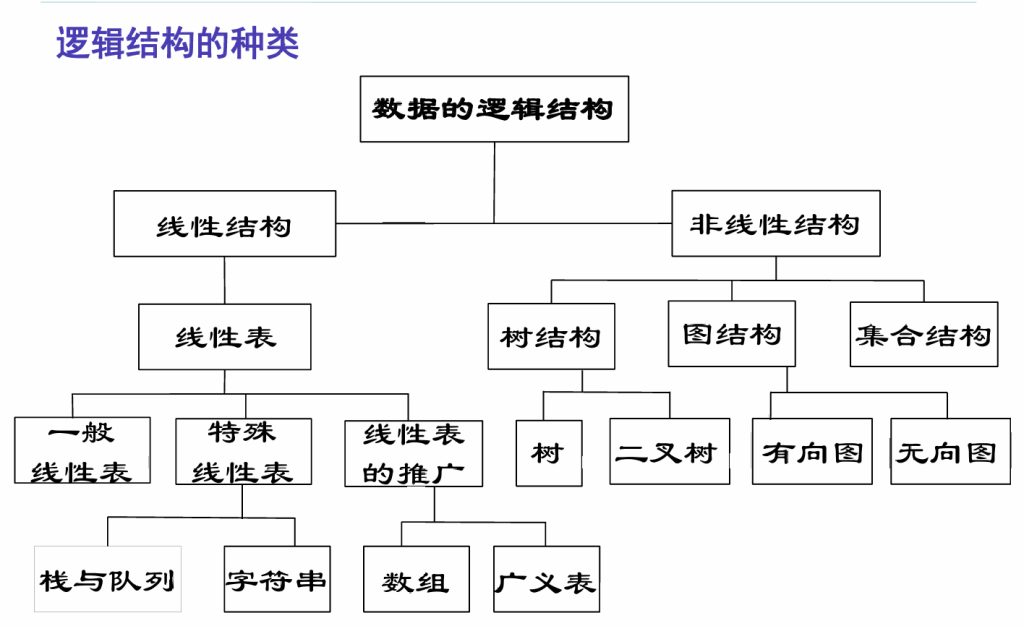
• 物理结构（存储结构）：是数据的逻辑结构在计算机存储器中的表示，包括数据元素的表示和关系的表示

• 数据的运算和实现，即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现

算法的设计取决于选定的数据逻辑结构，算法的实现依赖于采用的存储结构

例子解释

数据元素：把 “整个学校的学生信息（数据）” 看作一个整体，那么数据元素就是学校里的每一个学生，比如学生甲、学生乙等，每个学生都是组成学校学生信息这一 “数据” 的基本单位，如同集合里的单个个体

数据对象可以理解为从全校学生中，选取出来的、性质相同的一部分学生。比如，只选取高一年级（1）班的所有学生（这些学生都具有 “高一年级（1）班学生” 的相同性质），这一整个班级的学生就构成了一个数据对象。而这个班级的学生（数据对象）是全校学生（数据）的一个子集，即集合的子集

把 “学生” 看作数据元素，数据结构就是这些学生按照一定关系组织起来的集合。比如，在班级里，学生之间存在 “同桌关系”“前后排关系” 等特定关系

从集合论二元组角度：

• D（数据元素的有限集）：假设我们选取的班级学生是有限的，比如有 40 名学生，那么 D 就是由这 40 名学生这些数据元素组成的有限集合。
• S（D 上关系的有限集）：在这 40 名学生（D 中的元素）之间，存在的关系也是有限的。比如 “学生 A 是学生 B 的同桌”“学生 C 在学生 D 的前排” 这些关系，所有这样的关系组成的集合就是 S。那么整个数据结构 Data_Structure 就由这 40 名学生（D）以及他们之间的同桌、前后排等关系（S）组成，即 Data_Structure = (D, S)。

数据类型 data type

定义：一组性质相同的值的集合以及定义在这个值集合上的一组操作的总称
数据类型=值的集合+值集合上的一组操作

高级语言中的数据类型明显地或隐含地规定了在程序执行期间变量和表达的所有可能的取值范围，以及在这些数值范围上所允许进行的操作

• 例如，C语言中定义变量i为int类型，就表示i是在[-min, max]范围内的整数，在这个整数集上可以进行+,-,*,\等操作

数据类型的作用：
（1）约束变量或常量的取值范围
（2）约束变量或常量的操作

按“值”的不同特性，高级程序语言中的数据类型可分为两类：
一类是非结构的原子类型。原子类型（非结构类型）的值是不可分解的，例如C语言中的基本类型(整型、实型、字符型和枚举类型)、指针类型和空类型。
另一类是结构类型（包括数组、结构体、类、链表、集合、字典）。结构类型的值是由若干成分按某种结构组成的，因此是可以分解的，并且它的成分可以是非结构的，也可以是结构的。例如数组的值由若干分量组成，每个分量可以是整数，也可以是数组等。
结构类型可以看成由一种数据结构和定义在其上的一组操作组成。

抽象数据类型（Abstract Data Type，ADT）

是指一个数学模型以及定义在此模型上的一组操作

不考虑计算机内的具体存储结构与运算的具体实现算法

和数据类型实质上是一个概念，例如，各个计算机都拥有的“整数”类型是一个抽象数据类型，尽管它们在不同处理器上实现的方法可以不同，但由于其定义的数学特性相同，在用户看来都是相同的。因此，“抽象”的意义在于数据类型的数学抽象特性。

我的理解是只要满足值的逻辑结构相同（不管存储结构）和在值上的操作相同就可以被称为X抽象数据类型

抽象数据类型的表示与实现

一个问题抽象为一个抽象数据类型后，仅是形式上的抽象定义，还没有达到问题解决的目的，要实现这个目标，就要把抽象的变成具体的，即抽象数据类型在计算机上实现，变为一个能用的具体的数据类型

抽象数据类型可通过固有的数据类型（如整型、实型、字符型等）来表示和实现。利用处理器中存在的数据类型来说明新的结构，用已经实现的操作来组合新的操作

算法和算法分析

算法：解决某一特定问题的具体步骤的描述，是指令的有限序列。每个指令表示一个或多个操作。
考虑如何将输入转换成输出，一个问题可以有多种算法

程序是用某种程序设计语言对算法的具体实现，程序=数据结构+算法

一个算法具有以下5个特性：

1. 有穷性 一个算法必须总是(对任何合法的输入值)在执行有穷步之后结束，且每一步都可在有穷时间内完成。
2. 确定性 算法中每一条指令必须有确切的含义，读者理解时不会产生二义性。并且，在任何条件下，算法只有惟一的一条执行路径，即对于相同的输入只能得出相同的输出。
3. 可行性 一个算法是能行的，即算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现的。
4. 输入 一个算法有零个或多个的输入，这些输入取自于某个特定的对象的集合。
5. 输出 一个算法有一个或多个的输出，这些输出是同输入有着某些特定关系的量

算法设计的要求：

• 正确性：算法满足问题要求，能正确解决问题算法转化为程序后：

1. 程序中不含语法错误；
2. 程序对于几组输入数据能够得出满足要求的结果；
3. 程序对于精心选择的、典型、苛刻且带有刁难性的几组输入数据能够得出满足要求的结果；
4. 程序对于一切合法的输入数据都能得出满足要求的结果通常以第三层意义上的正确性作为衡量一个算法是否合格的标准

• 可读性：易于理解

1. 算法主要是为了人的阅读和交流，其次才是为计算机执行，因此算法应该易于人的理解；
2. 另一方面，晦涩难读的算法易于隐藏较多错误而难以调试

• 健壮性：能够处理非法数据、意外情况

1. 指当输入非法数据时，算法恰当地做出反应或进行相应处理，而不是产生莫名其妙的输出结果
2. 处理出错的方法，不应是中断程序的执行，而应是返回一个表示错误或错误性质的值，以便在更高的抽象层次上进行处理

• 高效性：对时效性和存储量的需求
• 一个好的算法首先要具备正确性，健壮性，可读性，在几个方面都满足的情况下，主要考虑算法的效率，通过算法的效率高低来评判不同算法的优劣程度
• 算法效率考虑两个方面√ 时间效率：算法所耗费的时间√ 空间效率：算法在执行过程中所耗费的存储空间时间效率和空间效率有时候是矛盾的

算法效率的度量

为什么不能用时间

多数情况下是最深层循环内的语句中的原操作的执行时间与算法的执行时间成正比（即该句的每次执行时间最接近单位时间）

为什么衡量算法要考虑n，而不是只看具体次数

衡量程序（算法）的效率时，上面提到直接用实际运行时间来评判并不合理

程序的执行时间本质上取决于算法中 “基本操作” （重复频率最高的操作）的总执行次数（执行时间 = 总执行次数 × 单条具体时间）。

算法的 “执行次数” 不是一个固定值，而是随 “问题有多大”（即问题规模 n）变化的，脱离问题规模谈 “执行次数” 是没有意义的。进一步说，当问题规模（用n表示，比如处理n个数据、n个节点等）变化时，基本操作的总执行次数会随之变化，且这种变化关系可以抽象为一个关于n的函数，记为T(n)。

通过T(n)，我们能清晰捕捉到 “算法工作量随问题规模增长的趋势”—— 这才是衡量算法效率的核心。比如，当n从 1000 增大到 10000 时，T(n)=n的算法工作量增长 10 倍，而T(n)=n²的算法工作量会增长 100 倍，显然前者的效率更优。这种趋势不受具体运行环境影响，能客观反映不同算法的本质差异。

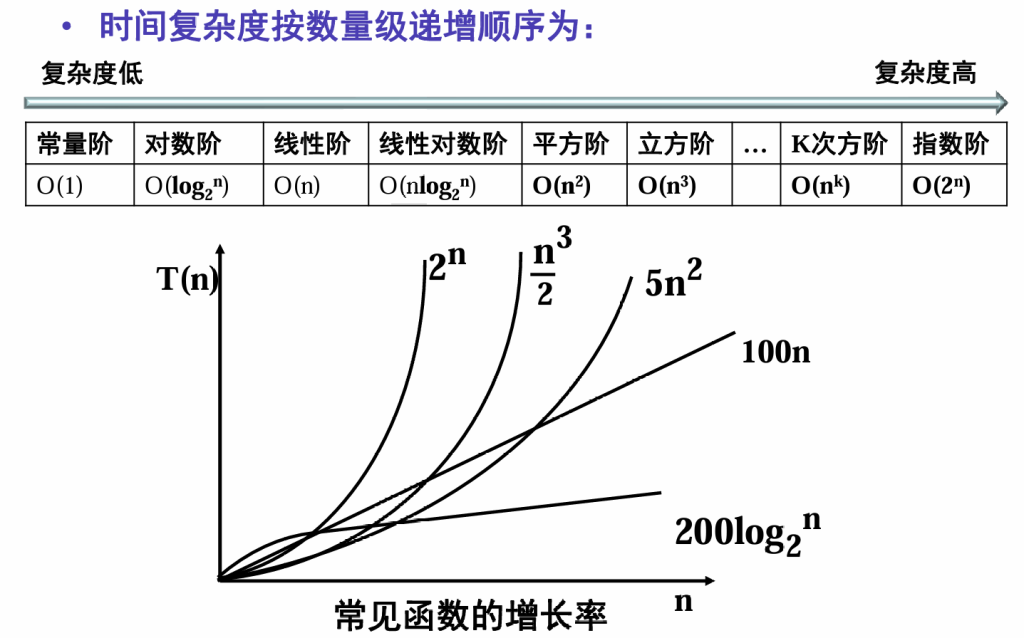
后续为了更简洁地描述这种趋势，我们会用 “大 O 表示法” 对T(n)进行简化（比如T(n)=n+5简化为O(n)，T(n)=3n²+2n简化为O(n²)），只保留函数中增长最快的项，从而快速判断算法在大规模问题下的效率表现。这一思路构成了算法时间复杂度分析的基础，也是计算机科学中衡量算法优劣的核心方法。

O时间复杂度表示T（n）

为了便于比较不同算法的时间效率，仅比较它们的数量级

计算时间复杂度例题

i=1; k=0;
while (i <=n-1) {
  @ k +=10 *i;
  i++;
}

i=1; k=0;
do {
  @ k +=10 *i;
  i++;
} while(i<=n-1);

i=1; k=0;
while (i <=n-1) {
  i++;
  @ k +=10 *i;
}

循环执行次数为 n-1 次（i 取 1 到n-1），因此频度为 \(n-1\)。

for(int i = 1; i <= n; i++){
    for(int j = i; j <= n; j++){
        // 循环体
    }
}

此时计算内层循环执行次数，当\(i = 1\)时，内层j从1到n，执行n次；当\(i = 2\)时，内层j从2到n，执行\(n – 1\)次；…… 当\(i = n\)时，内层j从n到n，执行1次。总的执行次数是\(n+(n – 1)+(n – 2)+\cdots+1=\frac{n(n + 1)}{2}\)

for(i=1; i<=n; i++) {
  for (j=1; j<=i; j++)
    for (k=1; k<=j; k++)
      @ x += delta;
}

i=1; j=0;
while (i+j <=n) {
  @ if (i>j) j++ ; else i++ ;
}

x=n; y=0;
while (x >= (y+1)*(y+1)) {
  @ y++;
}

x=91; y=100;
while (y>0) {
  @ if (x>100) {x-=10; y--;} else x++;
}