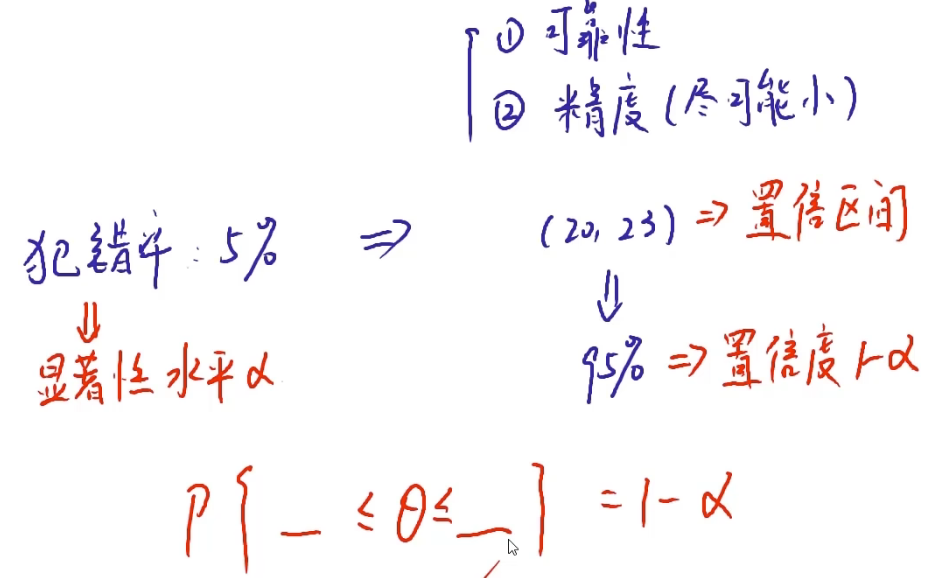描述性统计:
是在已经有全部数据的情况下,对这些数据进行总结、分析和呈现。
比如:你统计了全班学生的身高,然后算出平均身高、最大值、最小值,这就是描述性统计。
推断性统计:
是在只拿到部分样本数据的前提下,去推测整个总体的情况。
比如:你只随机量了全班 5 个同学的身高,就想估计全班的平均身高,这就是推断性统计。
实际上,研究人员几乎总是依赖样本 —— 即某个更大总体的有限子集。抽样理论通过明确如何从样本数据推断未知总体参数,架起了概率与推断之间的桥梁
统计学的两大基本问题:估计问题和假设检验问题,我们需要对我们说学习的统计学有个大体的框架,我们在算什么,在做什么,西面用一个例子讲清楚
你要采购10000个灯泡,老板要求这批灯泡的平均寿命必须大于4000h,这时你找到一个灯泡制作工厂
你并不知道这10000个灯泡的平均寿命是多少
我们知道最真实的平均寿命(被称为总体寿命)就是将这10000个灯泡全部测一遍寿命然后计算,但这不会破坏这些灯泡,所以我们需要估计总体寿命,所以我们从这10000个灯泡中采样100个灯泡,计算他们的平均寿命(被称为样本均值),通过计算我们得到一个平均寿命为4001h,
你抽了 100 个灯泡,算出样本均值\(\bar{X}=4001\)小时。但只报这个数老板不放心 ——“这 100 个能代表 10000 个吗?误差有多大?”
这时候就需要置信区间:它能告诉你 “总体均值大概率落在哪个范围里”。
假设我们算出样本标准差\(s=200\)小时(用贝塞尔校正后的无偏估计),根据统计学的中心极限定理,总体均值的 95% 置信区间公式为:
\(\bar{X} \pm t_{\alpha/2}(n-1) \cdot \frac{s}{\sqrt{n}}\)
(这里\(n=100\),\(n-1=99\),\(t_{\alpha/2}\)近似取 1.984,因为大样本下 t 分布接近正态分布)
代入计算:
\(4001 \pm 1.984 \cdot \frac{200}{\sqrt{100}} = 4001 \pm 1.984 \cdot 20 = 4001 \pm 39.68\)
即95% 的置信区间是 (3961.32, 4040.68) 小时。
它的含义是:“我们有 95% 的把握,这批 10000 个灯泡的真实平均寿命在 3961.32 到 4040.68 小时之间。” 这就把 “估计的不确定性” 量化了
以上是统计学的估计问题的解决过程,下面就是科学的决策到底要不要拒绝这批产品,在统计学中称为假设检验问题
老板要求 “平均寿命必须大于 4000h”,我们可以把它转化为假设检验:
- 原假设\(H_0\):总体平均寿命\(\mu \leq 4000\)(这批货不达标,该拒绝)
- 备择假设\(H_1\):总体平均寿命\(\mu > 4000\)(这批货达标,该接受)
接下来需要判断:样本均值\(\bar{X}=4001\)是 “偶然出现”,还是 “足以证明总体确实 > 4000”。
步骤 1:计算检验统计量
用 t 统计量(因为总体标准差未知,用样本标准差代替):
\(t = \frac{\bar{X} – \mu_0}{s/\sqrt{n}} = \frac{4001 – 4000}{200/\sqrt{100}} = \frac{1}{20} = 0.05\)
步骤 2:确定 “拒绝域”
我们设定显著性水平\(\alpha=0.05\)(即允许第一类错误的概率为 5%)。对于单侧检验(因为只要\(\mu>4000\)就达标),查 t 分布表(自由度 99),得临界值\(t_{0.05}(99) \approx 1.66\)。
如果计算的\(t > 1.66\),就拒绝\(H_0\)(认为达标);否则不拒绝\(H_0\)(认为不达标)。
这里我们的\(t=0.05 < 1.66\),所以不拒绝原假设\(H_0\)—— 也就是说,目前的样本证据不足以证明这批灯泡平均寿命 > 4000h,需要谨慎决策。
但是问题在于我们用100个样本点估计的值可能是错误的 ,但同时也有可能恰好是准确的,这里就引入了2个错误
假设你是概率之神,知道总体均值的值
第一类错误即估计值4001h是不准确的结果(真实为3900h)但你选择采用
这批灯泡真实平均寿命≤4000h(不达标),但我们错误地认为它 > 4000h 并采购了 —— 后果是买到次品,损失成本。
第二类错误即估计值40001h是准确的结果(真实也为4001h)但你选择不采用
这批灯泡真实平均寿命 > 4000h(达标),但我们错误地认为它≤4000h 并拒绝了 —— 后果是错过好货,损失商机。
我们在做决策时都有可能烦以上两个错误之一,但是我们尽可能的降低犯错的概率
统计学中,α 和 β 此消彼长:如果我们把 α 设得很小(比如 0.01),减少 “错买次品” 的概率,但会增加 “错拒好货” 的 β;反之如果 α 设得大(比如 0.1),减少 β,但增加 α。
在这个灯泡例子中,老板可能更怕 “买到次品”,所以会把 α 设得小一些(比如 0.01),宁愿多拒绝一些可能达标的批次,也要降低买到次品的风险。
总结:统计学框架的核心逻辑
- 估计问题:用样本算 “点估计”(如样本均值),再用 “置信区间” 量化估计的可靠性,回答 “总体参数大概在哪,准不准”。
- 假设检验问题:先提出关于总体的 “假设”,再用样本证据判断 “是否有足够理由推翻原假设”,回答 “决策是否合理”。
- 两类错误与权衡:明确决策的风险,根据实际场景(怕错买还是怕错拒)调整 α,让统计决策服务于业务目标。
抽样方法
简单随机样本
抽样方法定义了如何选择样本。最基本的是简单随机样本(SRS):
若总体中每个元素被选中的概率相等,且每个大小为 n 的可能样本被选中的可能性相同,则该样本为简单随机样本。
示例:假设有 10 个信封,每个标有唯一字母(A-J),其中 4 个装有折扣券。研究人员无放回地抽取 4 个信封。若每组 4 个信封被选中的概率相等,则这是一个 SRS。有放回抽样允许同一个信封被多次抽取,以确保独立性。
多数现实样本并非简单随机样本
在应用研究中,获取真正的简单随机样本通常不切实际。即使在狭窄定义的场景中(如从单一大学抽取学生),参与者也未必能真正代表目标总体的随机子集。因此,研究人员常依赖其他抽样策略,以下概述几种关键方法:
分层抽样
在分层抽样中,总体按已知特征(如地理位置、收入阶层或临床诊断)划分为互斥的子组(层),然后从每个层中随机抽样。这比简单随机抽样更高效,尤其当某些子组较罕见时。
示例:在评估工业污染健康影响的环境研究中,从整个城市随机抽样可能导致居住在污染源附近的参与者极少。为更好理解暴露影响,研究人员可将总体分为居住在工业区附近和较远的群体,然后对高暴露区域的个体进行过采样(有意过度代表)。
雪球抽样
当目标总体隐蔽或难以接触时,常使用雪球抽样。该方法从识别少量合格参与者开始,然后请他们推荐其他符合条件的人,如此递归直至达到所需样本量。
示例:在城市无家可归者研究中,研究人员可能先访谈少量街头流浪者,再请每位参与者推荐其他愿意参与的人,使样本通过人际网络扩展。
雪球抽样常用于研究流动性强或难以触及的群体,但其引入抽样偏差 —— 倾向于过度代表某些社交网络。
方便抽样
方便抽样指选择研究人员容易接触到的参与者,无论其代表性如何。这可能是心理学和社会科学中最常见的抽样形式。
示例:许多研究招募修读入门课程的本科生,这不仅将样本限制在狭窄的人口特征中,学生还可能因个人兴趣自行选择参与研究,引入更多偏差。
方便样本并非本质无效,但其推广性通常有限。研究人员必须仔细考虑其中的权衡,并在报告结果时透明说明抽样方法。
尽管简单随机样本仍是推断的黄金标准,但实际中很少能实现。研究人员常需在其他抽样方案中选择,每种方案各有优劣。认识抽样对推断的影响是开展可靠且可解释的统计分析的关键。
样本非随机是否重要?
情况并非绝对:有偏样本确实可能扭曲结论,但并非所有抽样偏差都有问题。
在某些情况下(如分层抽样),偏差是故意且已知的。这些技术通过确保子组的充分代表性,常能改善研究设计。此外,存在正式方法(本课程不涉及)可对这类偏差进行统计调整,使其影响降低。
核心观点是:随机抽样是手段而非目的。仅当有偏抽样方法对所研究的特定心理或科学现象引入扭曲时,才会成为问题。
示例:两项测量工作记忆容量的研究中,研究 1 从所有周一出生的人中随机抽样,研究 2 从单一国家人口中随机抽样。尽管研究 1 的限制看似随意,但尚无证据表明出生日期与工作记忆相关;而研究 2 可能引入无意的文化、教育或语言偏差 —— 这些因素可能影响记忆任务表现。矛盾的是,就所研究的认知特质而言,研究 1 的样本可能更能代表全球人口。
由此得出两条重要建议:
- 设计研究时,仔细考虑希望推广到的总体,并努力适当抽样。
- 评估使用方便样本的研究时,仅当能明确说明抽样程序如何引入相关偏差时,才进行实质性批判。
总体参数与样本统计量 Population Parameters and Sample Statistics
某概率分布(通常是正态分布),其总体均值 \(\mu = 100\),总体标准差 \(\sigma = 15\)。这些值称为总体参数,描述完整分布的特征。
现从该分布中随机抽取 \(n = 100\) 人的样本,可能得到如下数据:\(102, 97, 88, 110, 93, …, 105, 99, 91\) 从该样本可计算样本统计量,如样本均值 \(\bar{x} = 98.5\) 和样本标准差 \(s = 15.9\)。由于抽样过程中的随机变异,这些值通常与真实总体参数略有差异。
样本统计量是总体参数的估计量:
- 总体均值 \(\mu\) 由样本均值 \(\bar{x}\) 估计;
- 总体方差 \(\sigma^{2}\) 由样本方差 \(s^{2}\) 估计。
大数定律 The Law of Large Numbers
当样本量 \(N \to \infty\) 时,样本均值 \(\bar{X}_{N} \to \mu\)(即真实总体均值)。
在前面的例子中,\(N = 100\) 的样本均值与真实总体均值较为接近。但在许多应用中,需要更高的精度。
自然的解决方案是收集更大的样本。例如,从 \(\mu = 100\)、\(\sigma = 15\) 的总体中抽取 \(N = 10,000\) 人的智商样本,其样本均值和标准差很可能非常接近总体值。
均值的抽样分布和其他变量的抽样分布Sampling Distribution of the Mean
“样本平均值”本身也是一种随机变量,而这种随机变量的分布,就叫做样本均值的抽样分布。
假设你有一个很大的总体,比如:
一整个城市学生的数学成绩(太多了,不可能全统计)
你每次:
- 随机挑出 5 个学生(这是你的“样本”)
- 记录这 5 个人的平均分
- 然后把样本扔掉,重新再挑另外 5 个人,再算一个平均分
你不断重复这个过程,比如上千次,就会得到很多个**“样本平均数”**。
这些“平均数”组成的分布,就是所谓的:样本均值的抽样分布
其他统计量的抽样分布
抽样分布不仅限于均值。任何样本统计量(如中位数、最大值或方差)都有对应的抽样分布,描述该统计量在重复样本中的变化。例如,若每次实验记录 5 个抽样个体的最大智商,则最大值得抽样分布往往右偏,因为最大值通常超过总体均值。
中心极限定理(CLT)
统计学的基本结论之一是中心极限定理(CLT),它描述了样本量增大时均值抽样分布的行为。

定理 1 蕴含三个关键事实:
- \(\bar{X}_{N}\) 的抽样分布以真实均值 \(\mu\) 为中心;
- 抽样分布的标准差称为标准误(SE),即 \(SE = \frac{\sigma}{\sqrt{N}}\);
- 当 N 增大时,无论原始总体分布形状如何,抽样分布近似正态。
这解释了为何正态分布在统计推断中如此普遍:即使总体非正态,随着 N 增大,均值的抽样分布仍趋向正态。这一性质使我们能利用正态分布近似构造置信区间和进行假设检验。
样本均值,样本方差估计总体均值,总体标准差(贝塞尔修正)

我们可以把 “总体” 想象成一个超大的班级,里面有所有学生;“样本” 就是从这个大班里抽出来的一小部分学生。
1. 估计总体均值
比如想知道整个大班学生的平均成绩(总体均值\(\mu\)),我们就抽 100 个学生(样本)来考试,算出这 100 人的平均分(样本均值\(\bar{X}\),比如 98.5 分)。这个样本平均分就是对总体平均分的最佳猜测,这就是 “点估计”。
显然,真实总体均值 \(\mu\) 可能不同(如 97.2 或 103.5),但基于样本,当前最佳估计值即为样本均值本身。这是点估计的核心:使用从样本计算的统计量,对未知总体参数形成最佳猜测。具体可表示为:\(\hat{\mu} = \bar{X}\)。
2. 估计总体标准差(为什么要 “贝塞尔校正”)
标准差是用来衡量数据 “离散程度” 的,比如成绩是都集中在 90 分左右,还是有的考 100、有的考 50。
- 假如只抽 1 个学生(样本只有 1 个),成绩是 20 分。那样本均值是 20,样本标准差算出来是 0—— 但这显然不对,因为总体里肯定有其他分数,只看 1 个就说 “没差异”,是严重低估了实际的离散程度。
- 再比如抽 2 个学生,成绩 20 和 22,样本均值 21,按普通公式算标准差是 1,但这还是低估了总体的变异(因为总体里还有更多不同的分数)。
问题出在:用样本算标准差时,如果直接除以样本量n,会系统性地低估总体的真实变异。为了纠正这个偏差,就需要 “贝塞尔校正”—— 把分母从n改成\(n-1\)。
简单说,样本量越小,不校正的偏差越明显;通过除以\(n-1\),能让样本标准差更准确地估计总体标准差。
因为从总体中抽样这个过程会让数据进一步集中,而低估总体方差(因为方差越大说明数据的离散程度越大)。所以为了增大样本方差,应该处以一个比n更小的数字,所以选择n-1
为什么除n-1而不是n-2、3…
因为用除以n-1的样本方差估计总体方差是无偏估计,并不说完全没有偏差,而是满足下面这个式子ES ^2..

置信区间估计 Confidence Interval
在应用统计中,点估计(如 \(\hat{\mu} = \bar{X}\))为未知总体参数提供单个最佳猜测,但任何基于有限样本的估计都存在不确定性。仅有点估计无法说明该猜测的精确程度。
为此,我们引入置信区间概念:用样本数据,去估计总体参数(比如总体均值 μ)可能落在某个范围内,而不再是某个点,这种估计方法称为区间估计
区间估计:

- 置信度 1- /(alpha/) – 正确率
- \显著性水平 /(alpha/) – 错误率
对于区间我们有两个要求:
- 可靠性
- 精度,要让这个区间尽可能的小
但这两个要求是矛盾的,提高精度,必然会降低可靠性,犯错的概率会变大。
在保证可靠性的前提下尽可能提高精度,因为其相比精度来说更重要,区间可以很宽泛,但至少不能错误率很大
它表达的是:
例:“我不确定总体参数到底是多少,但我可以说:我有 x% 的把握,它就在这个区间里。”
你抽取了一个样本,计算出平均身高是 170 cm,你希望估计整个学校男生的平均身高(μ)。
你可能会说:
“我不能确定 μ 是多少,但我有 95% 的信心,它落在 168 cm 到 172 cm 之间。”
这个 168,172 就是一个 95%置信区间。犯错率是5%
真实数据落在区间的正确率就是置信度,犯错率即不落在区间的正确率就是显著性水平



构造均值的置信区间(方差已知)

我们的确无法写出目标式子即u的范围,但是我们知道其Z分布的范围,只要将其不等式中间的Z换回u就可以得到u的范围了
不管什么未知,目标是一致的,就是写出下面这个式子
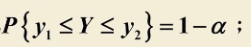
构造均值的置信区间(方差未知)
构造总体均值 \(\mu\) 的置信区间时,方法取决于总体标准差 \(\sigma\) 是否已知:


正态总体下σ² 的区间估计(置信区间) (均值已知)

σ² 的置信区间(均值未知)

置信区间公式总结