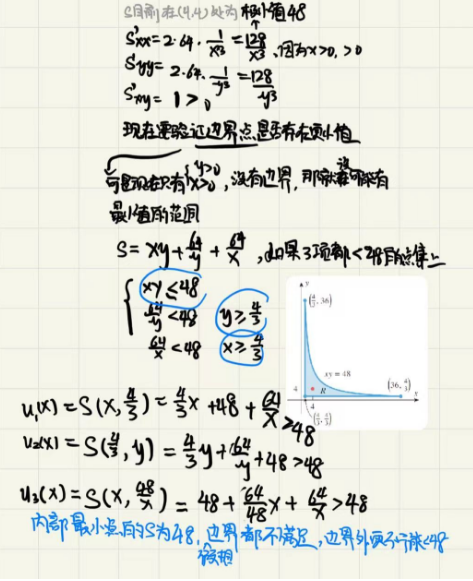
相对极大、相对极小，绝对极大、绝对极小值定义

定义：若二元函数f在点\((x_0, y_0)\)处存在一个以该点为中心的圆盘，使得对于圆盘内的所有点\((x, y)\)，都有\(f(x_0, y_0) \geq f(x, y)\)，则称f在点\((x_0, y_0)\)处有一个相对极大值；若对于f定义域内的所有点\((x, y)\)，都有\(f(x_0, y_0) \geq f(x, y)\)，则称f在点\((x_0, y_0)\)处有一个绝对极大值。

定义：若二元函数f在点\((x_0, y_0)\)处存在一个以该点为中心的圆盘，使得对于圆盘内的所有点\((x, y)\)，都有\(f(x_0, y_0) \leq f(x, y)\)，则称f在点\((x_0, y_0)\)处有一个相对极小值；若对于f定义域内的所有点\((x, y)\)，都有\(f(x_0, y_0) \leq f(x, y)\)，则称f在点\((x_0, y_0)\)处有一个绝对极小值。

若f在点\((x_0, y_0)\)处有相对极大值或相对极小值，则称f在点\((x_0, y_0)\)处有一个相对极值；若f在点\((x_0, y_0)\)处有绝对极大值或绝对极小值，则称f在点\((x_0, y_0)\)处有一个绝对极值。

极值定理 Extreme-value Therom：若\(f(x, y)\)在闭有界集R上连续，则f在R上既有绝对极大值，又有绝对极小值。

判断和求解二元函数的相对极值

若一元函数g在可导点\(x_0\)处有相对极值，则\(g'(x_0) = 0\)。对于二元函数，有类似的结论：

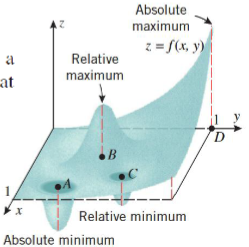
定理：若f在点\((x_0, y_0)\)处有相对极值，且f在该点处的一阶偏导数存在，则：
$$f_x(x_0, y_0) = 0 且  f_y(x_0, y_0)= 0$$

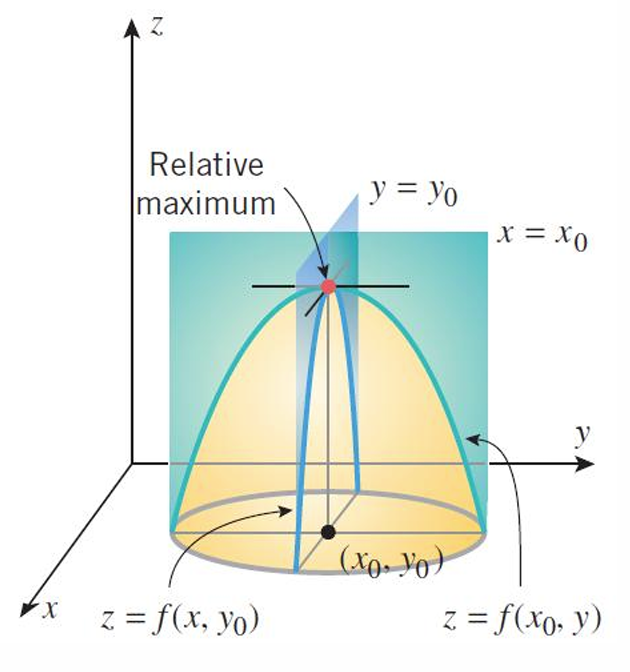
从几何上看，曲面\(z = f(x, y)\)在平面\(x = x_0\)和\(y = y_0\)上的截痕在点\((x_0, y_0)\)处有水平切线

临界点critical point 和 鞍点saddle point

一元函数f的临界点是指f定义域内使得\(f'(x) = 0\)或f不可导的那些x值。下为二元函数中临界点的定义

若点\((x_0, y_0)\)在函数\(f(x, y)\)的定义域内，且满足\(f_x(x_0, y_0) = 0\)且\(f_y(x_0, y_0) = 0\)，或者其中一个或两个偏导数在点\((x_0, y_0)\)处不存在，则称点\((x_0, y_0)\)为函数f的一个临界点。

例如：函数\(f(x, y) = y^2 – x^2\)，其图像是如图所示的双曲抛物面，在点\((0, 0)\)处有一个临界点，因为： \(f_x(x, y) = -2x\) 且 \(f_y(x, y) = 2y\) 由此可得： \(f_x(0, 0) = 0\) 且 \(f_y(0, 0) = 0\)

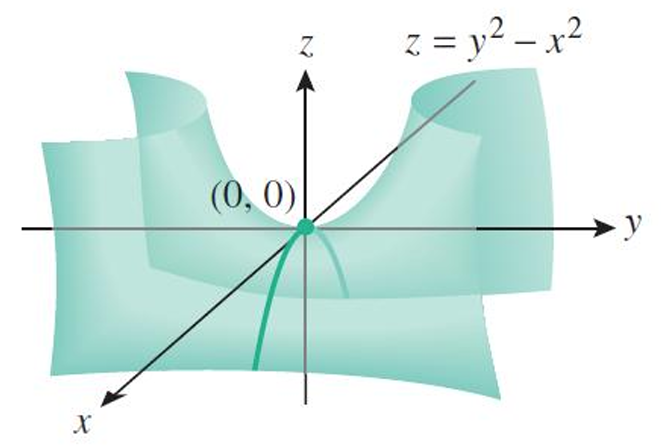
然而，函数f在点\((0, 0)\)处既没有相对极大值，也没有相对极小值。由于显而易见的原因，点\((0, 0)\)被称为f的鞍点。

鞍点定义：点\((x_0,y_0)\)是鞍点（saddle point），当满足： 虽然\((x_0,y_0)\)是函数的一个临界点，即 \[f_x(x_0,y_0) = 0, \quad f_y(x_0,y_0) = 0\] 但存在两个不同的垂直平面，使得曲面在其中一个平面上的截痕在点\((x_0, y_0)\)处有相对极大值，而在另一个平面上的截痕在点\((x_0, y_0)\)处有相对极小值

二阶偏导数检验法：

设f是二元函数，在以临界点\((x_0, y_0)\)为中心的某个圆盘内具有连续的二阶偏导数，且令： \(D = f_{xx}(x_0, y_0)f_{yy}(x_0, y_0) – f_{xy}^2(x_0, y_0)\)

(a) 若\(D > 0\)且\(f_{xx}(x_0, y_0) > 0\)，则f在点\((x_0, y_0)\)处有相对极小值。

(b) 若\(D > 0\)且\(f_{xx}(x_0, y_0) < 0\)，则f在点\((x_0, y_0)\)处有相对极大值。

(c) 若\(D < 0\)，则f在点\((x_0, y_0)\)处有鞍点。

(d) 若\(D = 0\)，则无法得出结论。

例1：

例2：

绝对极值

定理：若二元函数f在其定义域的一个内点处有绝对极值（绝对极大值或绝对极小值），则这个极值出现在一个临界点处。

如何在闭有界集R上求连续函数f的二元绝对极值

• 步骤 1：找出f在R内部的临界点。
• 步骤 2：找出所有可能出现绝对极值的边界点。
• 步骤 3：在上述步骤中得到的点处计算\(f(x, y)\)的值。这些值中的最大值是绝对极大值，最小值是绝对极小值。

例：确定一个顶部开口的长方体盒子的尺寸，其体积为\(32 ft^3\)。

解：设x = 盒子的长度（单位：英尺），y = 盒子的宽度（单位：英尺），z = 盒子的高度（单位：英尺），S = 盒子的表面积（单位：平方英尺）。

我们可以合理地假设，表面积最小的盒子需要的材料最少，因此我们的目标是最小化表面积： \(S = xy + 2xz + 2yz\) (5)

满足体积要求： \(xyz = 32\) (6)

由 (6) 我们得到\(z = 32 / xy\)，因此 (5) 可以改写为： \(S = xy + \frac{64}{y} + \frac{64}{x}\)

定义域：二维平面中 x>0,y>0。这个区域既不是闭的也不是有界的，由于这个区域不是闭集也不是有界集 ⇒ 不能用极值定理保证极小值一定存在，虽然不能保证存在，但我们可以说：
如果极小值存在，那它一定出现在函数的临界点（或趋近于边界）所以继续：求偏导 → 解临界点

解临界点：对 (7) 求导，我们得到： \(\frac{\partial S}{\partial x} = y – \frac{64}{x^2}\)，\(\frac{\partial S}{\partial y} = x – \frac{64}{y^2}\)

所以S的临界点的坐标满足： \(y – \frac{64}{x^2} = 0\)，\(x – \frac{64}{y^2} = 0\)

解第一个方程求y，得到： \(y = \frac{64}{x^2}\) (9)

将这个表达式代入第二个方程，得到： \(x – \frac{64}{(64 / x^2)^2} = 0\)

这可以改写为： \(x\left(1 – \frac{x^3}{64}\right) = 0\)

这个方程的解是\(x = 0\)和\(x = 4\)。由于我们要求\(x > 0\)，所以唯一有意义的解是\(x = 4\)。将这个值代入 (9)，得到\(y = 4\)。我们得出点\((x, y) = (4, 4)\)是S在第一象限中唯一的临界点。由于如果\(x = y = 4\)，\(S = 48\)，这表明我们试图证明S在开第一象限中的最小值是 48。

基于临界值对应的最小值，由于 x>0,y>0没有边界，我们没法验证边界点是否具有更小的面积值，所以我们基于目前的最小面积划分一个上限，与 x>0,y>0构成一个封闭的区域