一元函数
可微，可导，连续在一元函数中的定义
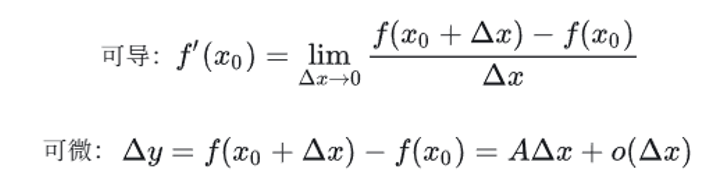
A代表某个导数(证明如下)，可微表达式不写出A具体是多少，因为其代表存在一个切线能用来近似x0处的函数，但我不关心具体切线的表达式，想起很久以前学到的，可微代表这里存在导数，但具体是多少我们需要求导得知。
证明一元函数中可导和可微等价
可导一定连续，连续不一定可导 =可微
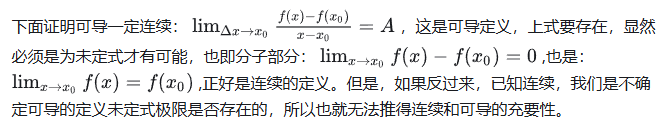
例子：
二元函数
二元函数和一元函数之间的差异主要源于极限（连续可导可微甚至可积的定义都和极限相关），在一元函数中，趋近方向只有两个，也即左、右，因此邻域只是一个小区间（类似线段）。但在二元函数中，趋近一个值可以有无数个方向，所以邻域是一个小圆（类似于一个圆面）。
可微(全微分)，可导(等价于可偏导)，连续在多元函数中的定义
可微(全微分)：
从能找到某个切线A，到找到某个由X方向和Y方向各自的切线所构成的切面。可微意味着函数所代表的曲面在该点附近是“光滑”的，可以用一个平面（切平面）很好地逼近函数趋近于(x0,y0)点的行为
，需要满足所有偏导数存在且在该点连续。
\(A = \frac{\partial f}{\partial x}\big|_{(x_0,y_0)}\) ，\(B = \frac{\partial f}{\partial y}\big|_{(x_0,y_0)}\) ，也就是A和B分别是函数\(f(x,y)\)在点\((x_0,y_0)\)处关于x和y的偏导数 。
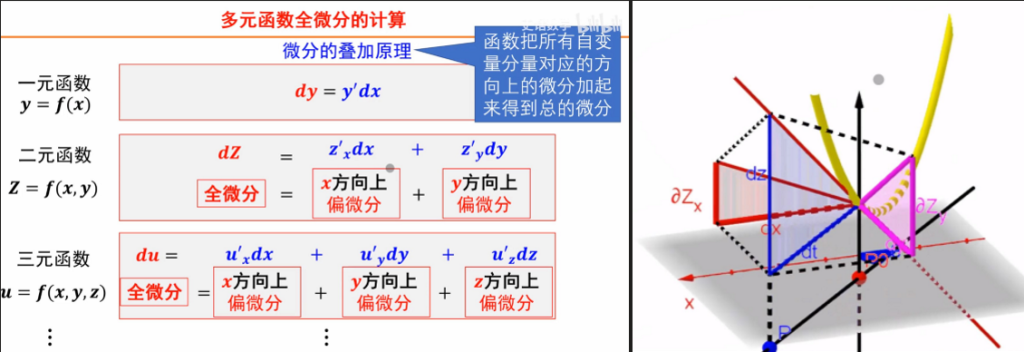
偏导数 = 导数，一元函数只有X轴这一个方向所以直接称为导数，不用说明”偏”以区分方向。但多元函数，必须要指定一个方向求变化率，如果选择求坐标轴方向的导数则为偏导数，选择任意方向的导数则为方向导数，偏导数是方向导数的特例。
连续：从趋向于X变为某个点时，x变化趋于0时y变化也趋于0
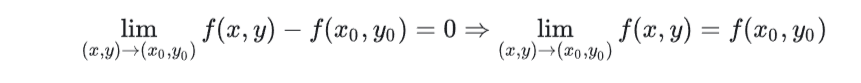
连续不可推全微分/可偏导 – 一笔可能不光滑
其实很明显，一笔画画出的无论多少维度的线都可以是非光滑的，所以连续无论什么情况下都无法推得偏导和可微
可微一定可偏导，可微一定连续 – 所有可以推1
可偏导不一定可微，可偏导不一定连续 – 1无法推所有
这里用例子说明：可微代表这里存在一个切面可以用来近似函数趋近于(x0,y0)点的行为，所以只有所有方向导数都存在且构成了该面才可以推出全微分，偏导数只是某个方向的切线，不足以说明整个面的存在性，同样连续也是要求函数沿着无数方向趋近某个点的极限存在且等于该点函数值，从几何上就是曲面该点处没有“洞”或者“裂缝”但可偏导却只能保证沿着平行于坐标轴的方向趋近是存在的
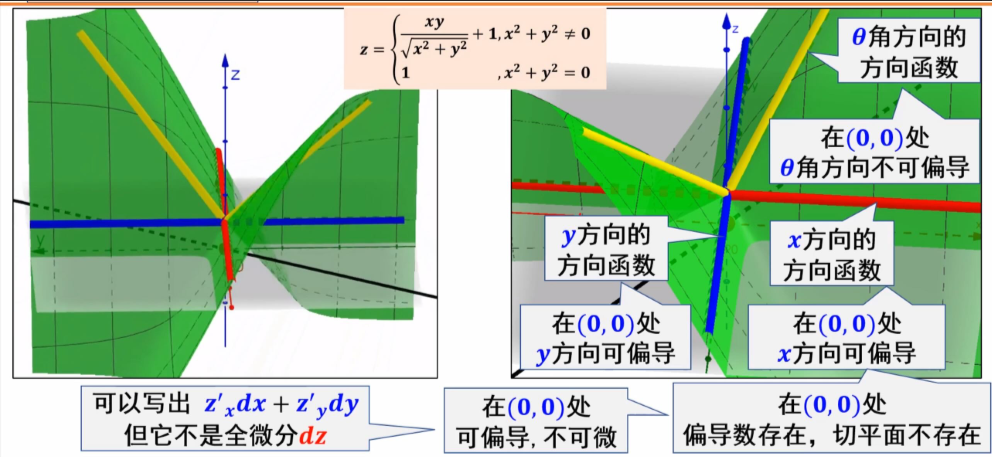
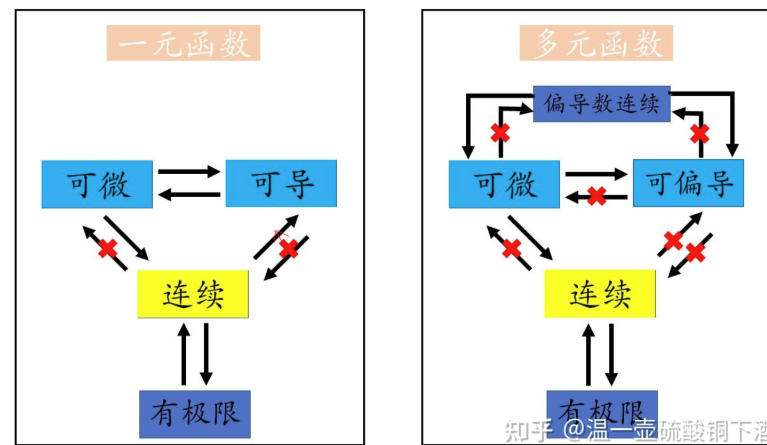
判断是否可微
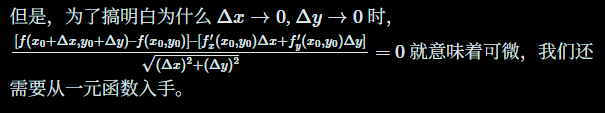
Reference:
