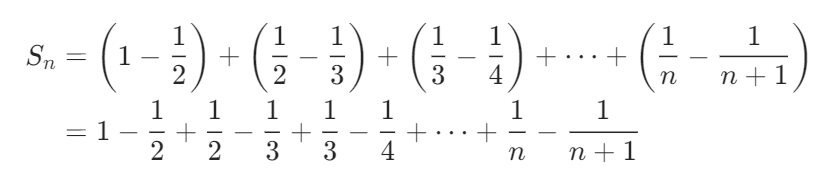Reference:
Cluster 聚类/簇
是一种无监督机器学习技术,用于在没有预定义标签的情况下将相似的观测数据分组。与监督学习不同(监督学习使用标记数据进行预测),聚类旨在发现数据中的隐藏结构。
在数据分析和统计学中,Clusters 指的是数据集中具有相似特征的子群体。聚类算法通过将观测数据分配到不同的组(簇)中,使得同一簇内的数据点彼此之间的相似度高于其他簇中的数据点。
Correlation 相关性 与 Causality(因果关系)
Causality 指一个事件(因)直接导致另一个事件(果)发生的机制,强调“原因和结果”的定向关系。
Correlation 描述两个变量之间的统计关联程度(同向或反向变化),但不涉及因果解释。
在统计学中,一个常见的错误是将相关性误解为因果关系。如果两个变量的变化趋势一致,则称它们具有相关性。然而,仅凭相关性并不能说明一个变量的变化导致了另一个变量的变化。
关系类型
- 正相关(r>0):两个变量同时增加(例如,学习时间与考试成绩)。
- 负相关(r<0):一个变量增加,另一个变量减少(例如,车速与行驶时间)。
- 无相关(r≈0):两者之间不存在有意义的关系。
为什么相关性不等于因果关系
相关性无法直接推导出因果关系,主要原因包括以下几点:
- 混杂变量干扰 Confounding Variables:可能存在第三个变量同时影响两个相关变量。例如,空调销量与中暑病例数呈正相关,是因为两者都在高温天气下增加,而非购买空调导致中暑。
- 反向因果关系 Reverse Causality:有时因果方向可能相反。例如,是更高收入带来了健康改善,还是健康的人更容易获得高收入?
- 虚假相关性 Spurious Correlations:某些相关性纯属巧合,例如某年迪士尼乐园游客数量与好莱坞新片发行数量之间的关联
要确立因果关系,通常采用以下方法:
- 控制实验:证明因果关系的黄金标准,通过随机分配受试者到不同条件组(例如设置对照组和实验组来验证咖啡因是否增强记忆力)。
- 纵向研究:长期观测变量,分析一个变量的变化是否先于另一个变量的变化。
- 因果推断方法:如工具变量法和倾向得分匹配法等技术,可在观察性研究中控制混杂因素。
理解相关性与因果关系的区别,对于决策制定、学术研究和政策制定至关重要,能有效避免误导性结论。
习题6. (聚类)某数据集包含200人的身高(厘米)和体重(千克)。研究人员使用聚类算法根据身高和体重对个体进行分组。
(a) 解释在此场景中聚类的用途。
(b) 如果某个聚类主要由身高较高且体重较重的人组成,可能的现实解释是什么?
(c) 如果在聚类前对变量进行标准化,结果会如何变化?
解答.
(a) 聚类有助于识别数据中的自然分组,可用于理解模式、预测趋势或提供个性化建议。
(b) 这种聚类模式可能反映了年龄、性别、遗传或生活习惯的差异(例如运动员与非运动员)。
(c) 标准化确保不同尺度的变量(如身高和体重)在聚类过程中具有同等重要性。
习题7. (相关性与因果关系)一项研究发现,吃更多冰淇淋的人更容易晒伤。
(a) 解释这种关系是因果关系还是由混杂变量引起。
(b) 指出一个可能的混杂变量。
(c) 如何设计实验来确定吃冰淇淋是否会导致晒伤?
解答. (a) 这种关系更可能是由混杂变量引起,而非冰淇淋直接导致晒伤。
(b) 可能的混杂变量是气温:炎热天气下,人们更可能吃冰淇淋,也更可能在户外活动导致晒伤。
(c) 可设计随机对照实验,将参与者随机分为吃冰淇淋组和不吃冰淇淋组,同时控制日晒时间。如果仅冰淇淋消费导致晒伤,则可推断因果关系
习题8. (虚假相关)研究人员发现,家庭中宠物数量与书籍数量高度相关。
(a) 这是否意味着养更多宠物会导致人们拥有更多书籍?为什么?
(b) 可能的解释是什么?
(c) 如何检验这种相关是真实的还是巧合?
解答. (a) 不,两者相关并不意味因果关系。
(b) 可能的解释是家庭成员较多的家庭可能同时拥有更多宠物和书籍。
(c) 可通过更大样本检验,并在控制家庭规模后观察相关性是否依然存在。
习题9. (解读相关系数)考虑以下变量间的相关系数:
(a) 学习时间与考试成绩的相关系数为r=0.85,这说明什么?
(b) 鞋码与智力分数的相关系数为r=−0.02,这说明什么?
(c) 火灾现场消防员数量与火灾损失的相关系数为r=0.78,这是否意味着消防员导致更多损失?解释原因。
解答. (a) 强正相关(r=0.85)表明学习时间越长,考试成绩越高。
(b) 接近零的相关(r=−0.02)表明鞋码与智力无显著关系。
(c) 高相关(r=0.78)由混杂变量引起:更大火灾需要更多消防员,而非消防员导致更多损失。
习题10. (实验设计)科学家想研究听音乐是否有助于学生记忆更多信息。(a) 如何科学地验证这一假设?
(b) 为什么需要对照组?
(c) 研究中还应考虑哪些因素?
解答. (a) 可设计实验,一组学生边听音乐边学习,另一组在安静环境中学习,然后比较测试成绩。
(b) 对照组(不听音乐的学生)用于比较结果,判断音乐是否真的有效。
(c) 还应考虑材料难度、学生专注度和学习习惯等因素
Simpson’s Paradox 辛普森悖论
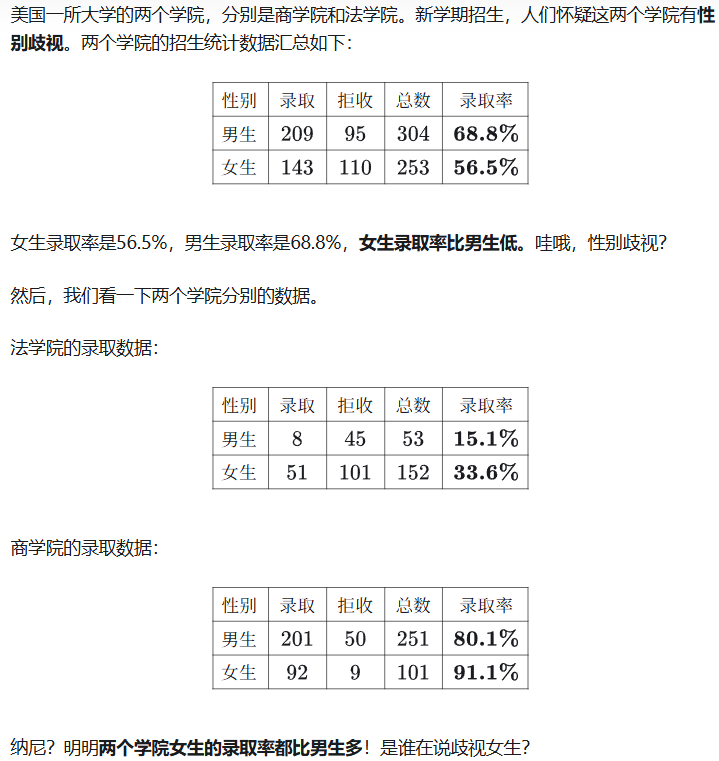
在上面美国大学录取这个例子里,出现这种情况,主要有两个原因:
- 两个学院录取率存在很大差距,法学院录取率低,商学院录取率高。然而不同性别的申请者的学院分布却相反。女性申请者大多分布在法学院,男性申请者大多分布在商学院。在数量上,拒收率高的法学院拒收了许多女生 (101人) ,虽然男生拒收率比女生高,但是男生被拒收的数量 (45人) 相对不算多。而商学院录取率高,导致男生被录取的数量比较多。因此最后的汇总结果,男生总的录取率比较高。
- 其他潜在因素的影响。性别并非是影响录取率的唯一因素,甚至可能对录取率毫无影响。或许是其他因素的作用,如入学成绩,教育背景等造成了录取率的差异,让人误以为是性别差异造成的。
这个例子告诉我们,辛普森悖论最重要的是告诉我们“相关”和因果关系之间不能画等号的
院系在这里是一个混淆变量 (confounding variable),它同时影响着男女生数量和录取率。
样本均值/方差和随机变量的期望/方差对比

- 样本均值 xˉ是实际观测数据的计算结果,是期望的估计值(当样本量 n→∞时,xˉ会收敛到 E[X],这是大数定律)
- 在期望公式中,概率 P(X=x)或密度函数 f(x)已经隐含了“加权平均”的作用(概率总和为1,相当于自动归一化)。而在样本均值中,每个数据点 xi 的权重是显式的1/n(因为假设样本是独立同分布的,每个点权重相同)。xi是具体的观测值(常数),不是随机变量(破案了)

- E[(X−E[X])2]是 理论方差,适用于随机变量。 样本方差,用于从实际数据中估计总体方差(无偏性要求除以 n−1)。两者本质相同,但应用场景不同:一个是理论值,一个是估计值。
Anscombe’s Quartet 安斯库姆四重奏

凸显了数据可视化的重要性——如果不绘制数据,仅基于汇总统计量,这些不同的分布会显得完全相同。
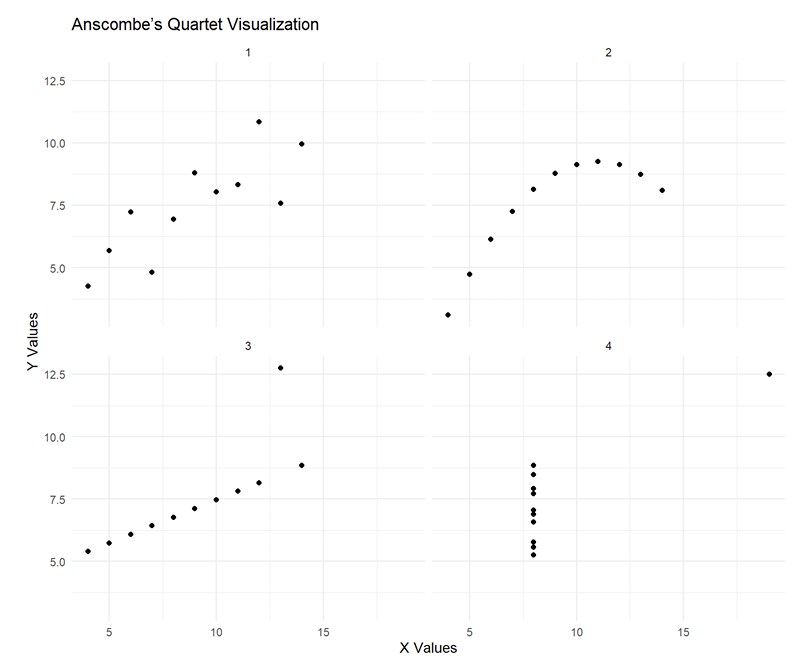
- 数据集1(左上):数据呈现线性趋势,带有一些方差。线性回归适用于此数据集。
- 数据集2(右上):数据呈现曲线(二次)关系。尽管相关性与其他数据集相同,但线性回归并不适用。
- 数据集3(左下):数据似乎呈现强线性关系,但一个离群值影响了回归线。
- 数据集4(右下):大多数点的x值相同,只有一个极端离群值。这个离群值极大地影响了相关性和回归结果,尽管实际上没有真正的趋势。
Correlation Coefficients 相关系数

相关系数(r)衡量两个变量之间的关联强度。值接近+1或-1表示强相关,而值接近0表示无相关性
条件概率

“given that” 引导的部分是条件 。在 “Compute the probability that an item is actually defective given that it failed the test.” 这句话中,“that it failed the test(物品测试未通过)” 是条件,即已知物品测试未通过这个前提

额外信息可以使事件的概率上升或下降,因为它改变了表示实验结果的样本空间。

partition 分割

为什么强调“{A,Ac}是分割”:说明任何事件及其补集都能将样本空间划分为两个“非重叠且完整”的部分
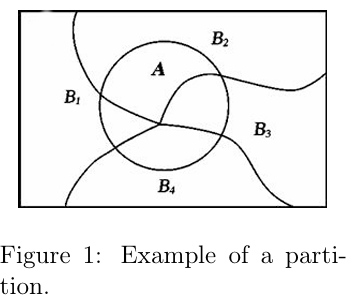

全概率公式
设 \(\{B_1, \cdots, B_k\}\) 为 \(\Omega\) 的一个分割。事件 A 的概率为:\[
\mathbb{P}(A) = \sum_{i=1}^k \mathbb{P}(A | B_i) \mathbb{P}(B_i)
\]一个特例是:如果 A 和 B 是两个事件,则:\[
\mathbb{P}(A) = \mathbb{P}(A | B) \mathbb{P}(B) + \mathbb{P}(A | B^c) \mathbb{P}(B^c)
\]
例1:用条件概率计算全概率

例2:不可重复的

贝叶斯定理
在已知结果的条件下,反推某个原因发生的概率,即逆向概率,用于更新先验概率。

例1:在参加多项选择题测试时,学生知道问题答案的概率为 pp,或者以概率 1−p1−p 猜测答案。每个问题有 mm 个选项。求学生在答对的情况下确实知道答案的概率公式,并在以下情况下计算其值:m=4 且 p=70% m=5 且 p=20%
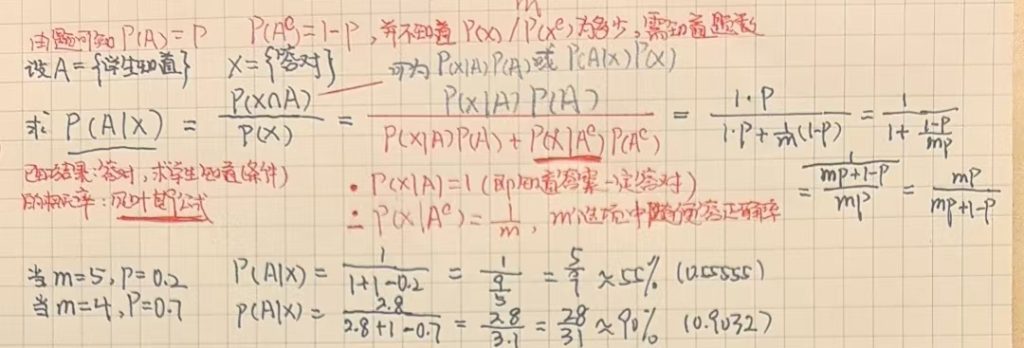
等式成立的原因是“知道答案时必然答对”(P(X∣A)=1,因此联合概率退化为 P(A)本身,即 p
例2:一家公司拥有机器 A、B和 C,均生产两种零件 X 和 Y。机器 A生产所有零件的60%,机器 B生产30%,机器 C生产10%。此外,A生产的零件中40%为 X,B 生产的零件中50%为 X,C 生产的零件中70%为 X。从该公司随机抽取一个零件。已知抽到的零件是 X,它分别来自机器 A、B 或 C 的概率是多少?

例3:

用一个例子感受全概率公式和贝叶斯公式的应用场景



排列组合 / 乘法原理

总结:

三门问题

Independent events 独立事件(乘法法则)
独立事件的条件概率等于自身,所以P(AB)也改写为P(A)与P(B)之积

例1:判断是否为独立事件,可以通过命题5中的任意一种进行判断,本质其实都是第二条
假设掷一枚公平硬币两次。以下情况下,事件 A 和 B是否独立?
1.) A={第一次掷出正面},B={两次结果相同}
2.) A={第一次掷出正面},B={第一次和第二次都掷出正面}

例2:

总和为6的所有有序对共有5种:(1,5),(2,4),(3,3),(4,2),(5,1)
- 其中 (3,3)是唯一一个两枚骰子点数相同的情况,因此只出现一次。
- 如果错误地认为 (3,3)应该算两次,就会得到6种情况(错误结果)。
两枚骰子的所有可能结果共有 6×6=36种,包括:
- 点数不同的有序对:如 (1,2),(1,3),…,(5,6) 等,共 6×5=30 种。
- 点数相同的有序对:如 (1,1),(2,2),…,(6,6),共6种。
因此,分母的36种结果中,(3,3)只出现一次,和其他重复点数(如 (1,1),(2,2)等)一样,均未被重复计算。
排列组合 (A(n,k)或 C(n,k)) 的结果比乘法原理少,是因为:
- 排列数 A(n,k)排除了重复情况(如 (1,1),(2,2))。
- 组合数 C(n,k)不仅排除了重复情况,还合并了顺序不同的情况(如 (1,2)和 (2,1)算一种)。
骰子问题必须用乘法原理,因为它需要 有序且可重复 的所有可能结果。
例3:
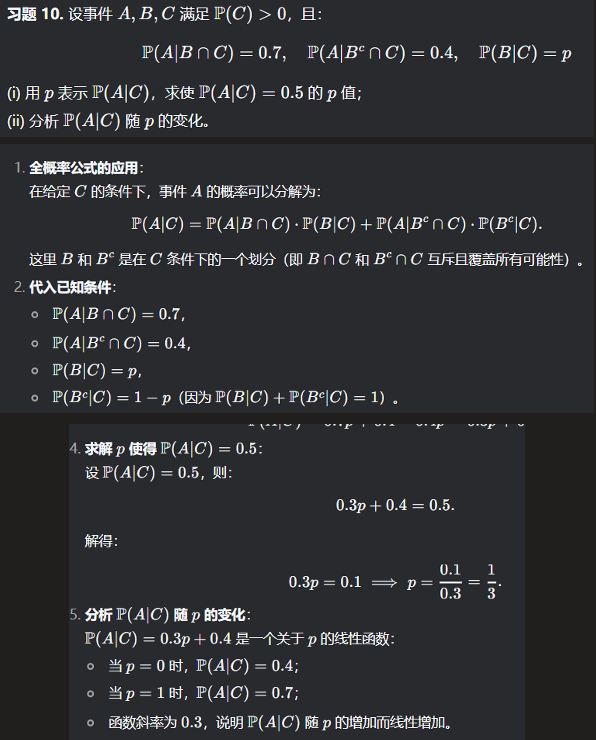
3个及以上独立事件
独立性:首先要求事件\((A,B)\)、\((B,C)\)、\((C,A)\)是独立的。三个事件\(A\)、\(B\)和\(C\)是 (集体) 独立的,另外还要求 \[ \mathbb{P}(A\cap B\cap C)=\mathbb{P}(A)\cdot\mathbb{P}(B)\cdot\mathbb{P}(C) \]该定义可以推广到四个或更多事件的情况。
定义 :事件\(A\)和\(B\)在给定\(C\)的条件下是条件独立的,如果 \[ \mathbb{P}(A\cap B|C)=\mathbb{P}(A|C)\cdot\mathbb{P}(B|C). \]
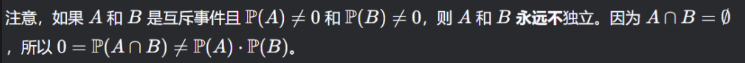
例1:

例2:

例3:

例4:



P(A^BC)即为P(A^B^C) , 另外 P(A/B) = P(A) – P(AB)
样本空间与随机变量
样本空间:实验结果的集合

概率质量函数


累积分布函数 Cumulative Distribution Function (CDF) 概率分布函数 probavility distribution
概率分布只是将值和对应的概率放在表中或分段函数中,累积分布函数,只是替换为小于等于该值的所有值的概率和作为对应值


计算经过函数变换后的新随机变量 Y=g(X)的概率分布
Y取某个值 y的概率,等于所有能让 g(x)=y的原始变量 X的概率之和。

例2:

随机变量的期望 / 期望值
计算随机变量 X经过函数 g变换后的平均值(期望值)
“函数 g(X)的期望,等于所有 X 的可能值代入 g 后,按概率加权求和


方差

独立事件的方差和期望
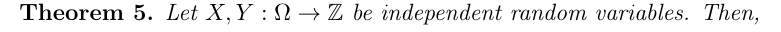
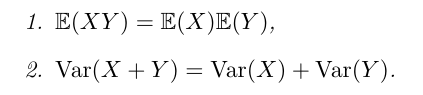
错题汇总:
自高中就经常想不到的思路:先固定顺序再排序以满足特定需求


反直觉,虽然每次排除一个选项,但是由于成功概率也下降,所以实际每次成功概率不变


看到A和A^C直接写全概率公式即可

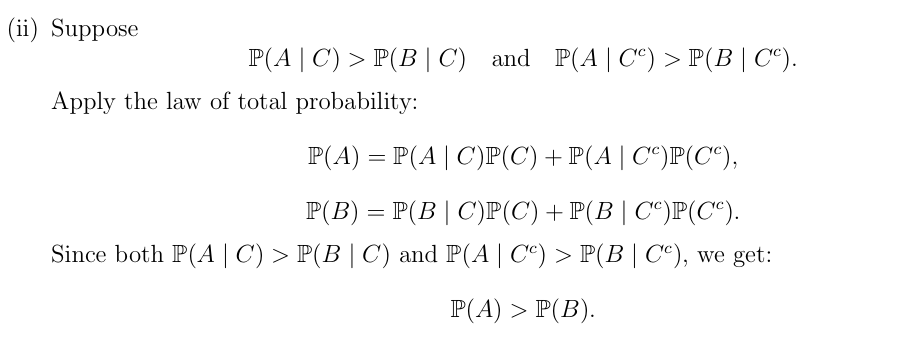
求问题的补集更容易

P(至少一天不是阴天) 转变为 1 -P(0天是阴天) P(最多4天是晴天) 转变为 1 -P(全部是晴天)
可以发现两者是一样的


验证概率质量函数是否合理