序列的表示

序列（Sequence）是指按照一定顺序排列的一组对象（通常是数）。序列中的每个对象称为项（Term）

序列的三种描述

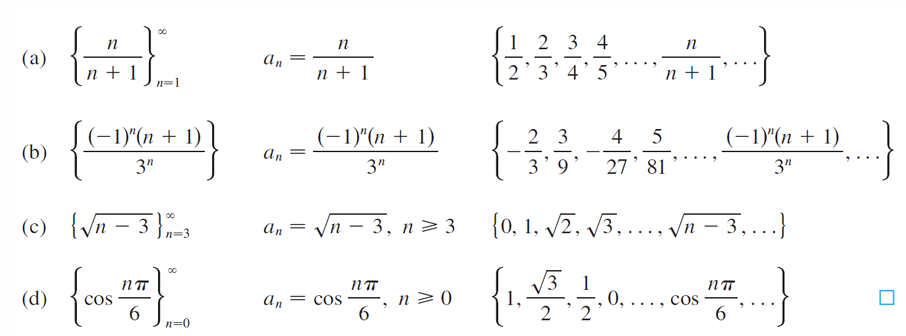
序列的极限和敛散性

序列\(\{a_n\}\)有极限 \(L\)，写作\(\lim_{n \to \infty} a_n = L\) 或 \(a_n \to L \text{ 当 } n \to \infty\)

如果 \((\lim_{n \to \infty} a_n)\) 存在，序列收敛。否则，序列发散

序列极限的运算法则

夹逼定理求序列极限

极限的连续性定理（Limit Continuity Theorem）

如果数列 \(\{a_n\}\) 的极限为 \(L\)（即 \(\lim_{n \to \infty} a_n = L\)），且函数 \(f\) 在点 \(L\) 处连续，那么：\[\lim_{n \to \infty} f(a_n) = f(L)\]
这一定理表明，在函数连续的条件下，极限运算可以“传递”到函数内部，即：\[\lim_{n \to \infty} f(a_n) = f\left(\lim_{n \to \infty} a_n\right)\]

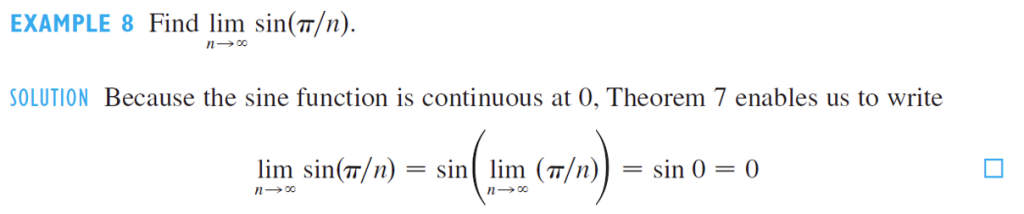
在计算复杂极限时，可以将极限运算与函数运算交换顺序，从而简化计算。

序列的单调性

The sequence \({r^n}\) is convergent if\(-1 < r \leq 1\) and divergent for all other values of \(r\).

$$\lim_{n \to \infty} r^n =
\begin{cases}
0 & \text{if } -1 < r < 1 \\
1 & \text{if } r = 1
\end{cases}$$

Bounded sequence 有界序列

Series 级数

数列的项相加所得到的和，给数列加一个求和符号即为级数。具体来说，给定一个数列 {an}，其级数可以表示为：

$$S = a_1 + a_2 + a_3 + \cdots = \sum_{n=1}^\infty a_n$$

级数s – 部分和sn = 余项Rn

对于一个无穷级数：\(\sum_{n=1}^{\infty} a_n = a_1 + a_2 + a_3 + \cdots\)

\( s_n \) 部分和：级数的前 \( n \) 项的和：\[s_n = a_1 + a_2 + a_3 + \cdots + a_n\]
\( R_n \) 余项(remainder)：级数的总和 \( s \) 与部分和 \( s_n \) 之差，即：\[R_n = s – s_n\]

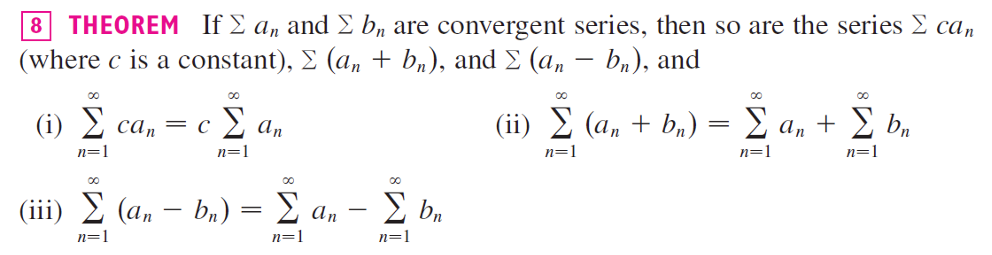
判断级数敛散性

给定一个级数 \(\sum_{n=1}^{\infty} a_n = a_1 + a_2 + a_3 + \cdots\)，令 \(s_n\) 表示其第 \(n\) 个部分和：
\[
s_n = \sum_{i=1}^{n} a_i = a_1 + a_2 + \cdots + a_n
\]

级数收敛的定义：部分和在无限项时趋于一个有限值

记作：
\[
a_1 + a_2 + \cdots + a_n + \cdots = s \quad \text{或} \quad \sum_{n=1}^{\infty} a_n = s
\]

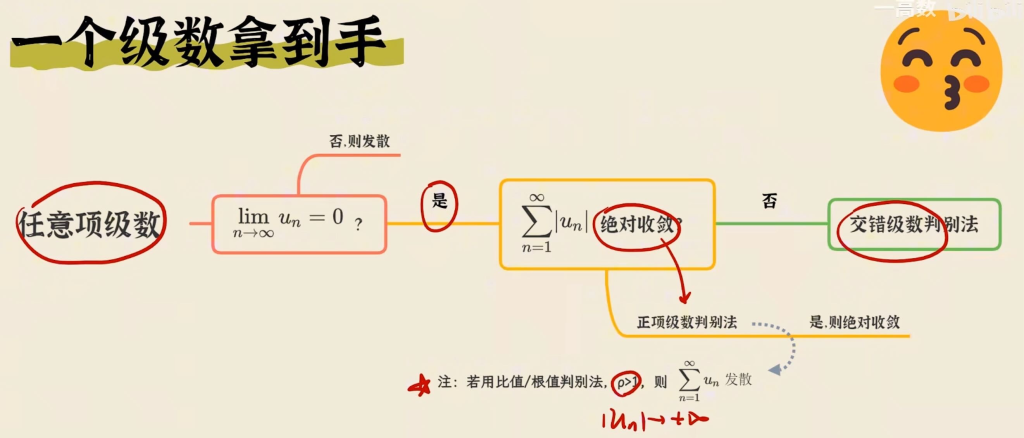
不建议按照特定顺序应用一系列检验，直到其中一个最终有效。那将是时间和精力的浪费。相反，与积分一样，主要策略是根据级数的形式对其进行分类

1. 如果你一眼就能看出 \(\lim_{n \to \infty} a_n \neq 0\)，则应使用发散检验。

2. 级数的形式为 \(\sum \frac{1}{n^p}\)，则它是一个 \(p\)-级数，我们知道当 \(p > 1\) 时收敛，当 \(p \leq 1\) 时发散。记巧：级数 \(\frac{1}{n^2}\) 比 \(\frac{1}{n}\) 衰减快得多，总和有限。

2. 级数的形式为 \(\sum a r^{n-1}\) 或 \(\sum a r^n\)，则它是一个几何级数，当 \(|r| < 1\) 时收敛，当 \(|r| \geq 1\) 时发散。可能需要进行一些初步的代数操作以将级数带入这种形式。记巧：指数函数图像

3. 级数的形式类似于 \(p\)-级数或几何级数，则应考虑使用比较检验之一。特别是，如果 \(a_n\) 是有理函数或 \(n\) 的代数函数（涉及多项式的根），则应将级数与 \(p\)-级数进行比较。请注意，练习 11.4 中的大多数级数都具有这种形式。（\(p\) 的值应如第 11.4 节所述，通过仅保留分子和分母中的最高次幂来选择。）比较检验仅适用于正项级数，但如果 \(\sum a_n\) 有一些负项，则我们可以将比较检验应用于 \(\sum |a_n|\) 并检验绝对收敛性

5. 级数的形式为 \(\sum (-1)^{n-1} b_n\) 或 \(\sum (-1)^n b_n\)，则交替级数检验是一个明显的选择。

6. 涉及阶乘或其他乘积（包括常数的 \( n \) 次幂）的级数通常可以方便地使用比值检验。请记住，对于所有 \( p \)-级数以及所有有理或代数函数，当 \( n \to \infty \) 时，\( |a_{n+1}/a_n| \to 1 \)。因此，比值检验不应用于此类级数。

7. 如果 \( a_n \) 的形式为 \( (b_n)^n \)，则根值检验可能有用。

8. 如果 \( a_n = f(n) \)，其中 \( \int_1^\infty f(x) \, dx \)易于计算，则积分检验是有效的（假设该检验的假设成立

定义法 – 写出Sn(不常用)

例1：

使用定义判断数列的敛散性时，通常需要先求出数列前n项的和（即部分和Sn）。对于等差数列和等比数列，我们可以直接应用已知的求和公式。但对于其他类型的数列，往往需要根据其通项特点，单独推导求和公式。例如下面这个例子……

例2：

该例子中，先将数列分式分解为2项，利用正负将中间项抵消，剩下首项和末项进而得到求和公式。用定义和更常用的是从定义推导出级数收敛的必要条件

级数收敛的必要条件 – 只用于判断发散

如果级数 \(\sum_{n=1}^\infty a_n\) 收敛，则 \(\lim_{n \to \infty} a_n = 0\)。

级数的极限为0，并不意味着级数的和一定为0。级数的和取决于所有项的累积效果，即使每一项都趋于0，它们的累积和仍可能趋近于一个非零的有限值，甚至可能发散到无穷大，比如调和级数：序列的极限趋于0，但是级数并不收敛，级数和为无限大。更常用的是其逆否命题

若 \(\lim_{n \to \infty} a_n \neq 0\)，则必有级数 \(\sum_{n=1}^{\infty} a_n\) 发散

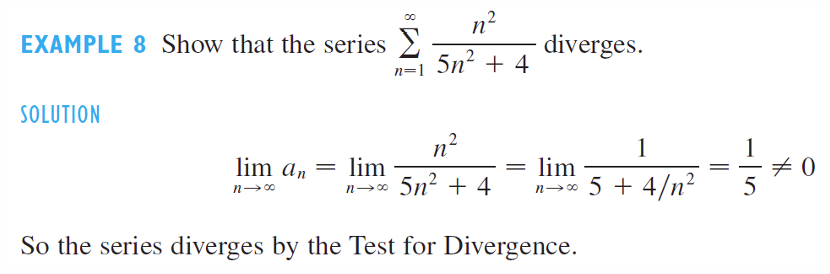
注意：如果 \(\lim_{n \to \infty} a_n = 0\)，我们对级数 \(\sum a_n\) 的收敛性或发散性一无所知。级数 \(\sum a_n\) 可能收敛，也可能发散

正项级数(每项都大于0) – 绝对收敛判别法

2个重要级数

P级数(包含调和级数(Harmonic Series))

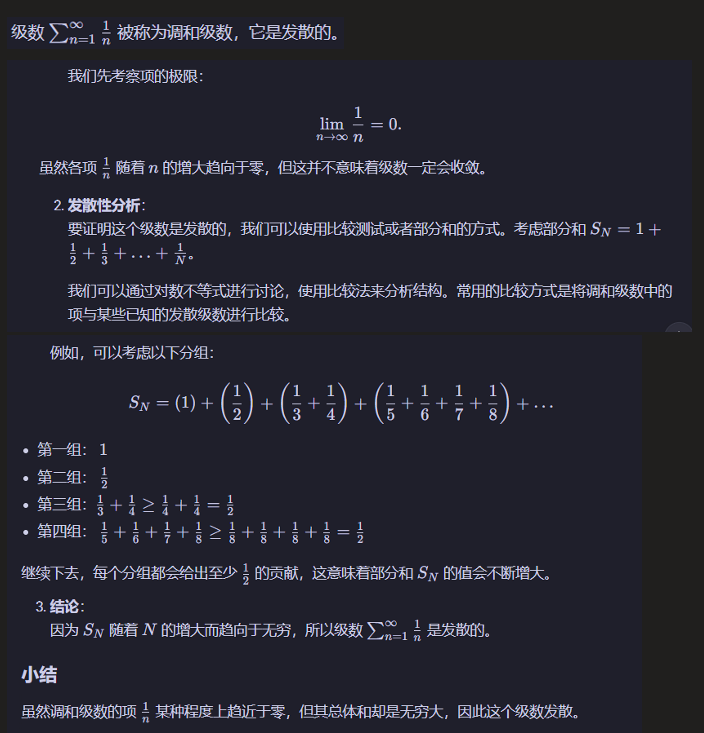
几何/等比级数

例子：\( \sum_{n=0}^{\infty} \frac{1}{2^n} = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots \)

几何级数的求和公式是由等比数列求和公式求得的，当公比小于1时r^n项趋于0所以省略。注意几何级数求和公式的2种表述，注意求和符号下的角标，保证是从x0开始

\[
\sum_{m=1}^{\infty} x^{m-1} = \sum_{n=0}^{\infty} x^n = \frac{1}{1-x}, \quad |x| < 1
\]\[
\sum_{m=1}^{\infty} m x^{m-1} = \frac{1}{(1-x)^2}
\]\[
\sum_{m=1}^{\infty} m^2 x^{m-1} = \frac{1+x}{(1-x)^3}
\]

证明：

几何级数求和公式：\[
\sum_{m=0}^{\infty} x^m = \frac{1}{1-x}, \quad |x| < 1
\]
对两边关于 \( x \) 求导，得到：\[
\sum_{m=1}^{\infty} m x^{m-1} = \frac{1}{(1-x)^2}
\]对上述次关于 \( x \) 求导，得到：
\[
\sum_{m=1}^{\infty} m(m-1) x^{m-2} = \frac{2}{(1-x)^3}
\]\[
\sum_{m=1}^{\infty} m^2 x^{m-2} – \sum_{m=1}^{\infty} m x^{m-2} = \frac{2}{(1-x)^3}
\]等式两边同乘 \( x \)：\[
\sum_{m=1}^{\infty} m^2 x^{m-1} = x \cdot \frac{2}{(1-x)^3} + \sum_{m=1}^{\infty} m x^{m-1}
\]\[
\sum_{m=1}^{\infty} m^2 x^{m-1} = \frac{2x}{(1-x)^3} + \frac{1}{(1-x)^2}
\]\[
\sum_{m=1}^{\infty} m^2 x^{m-1} = \frac{1+x}{(1-x)^3}
\] 继续增加m的次数再继续求导即可

Comparison 比较判别法

通过去掉低阶项保留高阶项得到的级数 / 已知级数与原级数相比得到敛散性

eg1：

eg2：通过去掉低阶项保留高阶项得到另一个级数

Determine whether the series \(\sum_{n=1}^{\infty} \frac{2n^2 + 3n}{\sqrt{5 + n^5}}\) converges or diverges.

The dominant part of the numerator is \(2n^2\) and the dominant part of the denominator is \(\sqrt{n^5} = n^{5/2}\). This suggests taking\[
a_n = \frac{2n^2 + 3n}{\sqrt{5 + n^5}} \quad \text{and} \quad b_n = \frac{2n^2}{n^{5/2}} = \frac{2}{n^{1/2}}
\]\[
\lim_{n \to \infty} \frac{a_n}{b_n} = \lim_{n \to \infty} \frac{2n^2 + 3n}{\sqrt{5 + n^5}} \cdot \frac{n^{1/2}}{2} = \lim_{n \to \infty} \frac{2n^{5/2} + 3n^{3/2}}{2\sqrt{5 + n^5}}
\]\[
= \lim_{n \to \infty} \frac{2 + \frac{3}{n}}{2\sqrt{5 / n^5 + 1}} = \frac{2 + 0}{2\sqrt{0 + 1}} = 1
\]Since \(\sum b_n = 2 \sum \frac{1}{n^{1/2}}\) is divergent (\(p\)-series with \(p = \frac{1}{2} < 1\)), the given series diverges by the Limit Comparison Test.

eg3：使用2个重要级数进行构造

尽管比较测试中的条件 \( a_n \leq b_n \) 或 \( a_n \geq b_n \) 对所有 \( n \) 给出，但我们只需要验证它对 \( n \geq N \) 成立，其中 \( N \) 是某个固定整数，因为级数的收敛性不受有限项的影响

测试级数 \(\sum_{n=1}^{\infty} \frac{\ln n}{n}\) 的收敛性或发散性。观察到 \(\ln n > 1\) 对于 \( n \geq 3 \)，因此

\[
\frac{\ln n}{n} > \frac{1}{n} \quad \text{对于} \quad n \geq 3
\]

我们知道 \(\sum \frac{1}{n}\) 是发散的（\( p = 1 \) 的 \( p \)-级数）。因此，给定级数通过比较测试发散。

比值Ratio 和根值 Root 判别法

比较法是找另一个级数，和自己比。此处是自己和自己比

例1：比值和根植判别

例2：级数中含有参数的情况需要分类讨论

积分测试 Integral Test

触发：当级数的通式形如一个可积分的函数时使用，且该函数首先要满足三个条件，恒正，单调递减，连续

当我们使用积分测试时，不必从 n=1 开始级数或积分。例如，在测试级数\(\sum_{n=4}^{\infty} \frac{1}{(n-3)^2}\) 使用 \(\int_{4}^{\infty} \frac{1}{(x-3)^2}\, dx\)

此外，函数 \( f \) 并不需要始终递减。重要的是 \( f \) 最终递减，即对于大于某个数 \( N \) 的 \( x \)，\( f \) 是递减的。那么 \( \sum_{n=N}^\infty a_n \) 是收敛的，因此 \( \sum_{n=1}^\infty a_n \) 也是收敛的。

交错级数 Alternating series – 条件收敛判别法

莱布尼兹判别法

易错，正项级数中的积分测试判别法，是要求lim定积分f(x)是否收敛，这里交错级数的莱布尼兹判别法要用limf(x)是否收敛

例1：有时需要通过求导函数判断局部单调性

先判断是否绝对收敛，再判断是否条件收敛还是收敛

总结

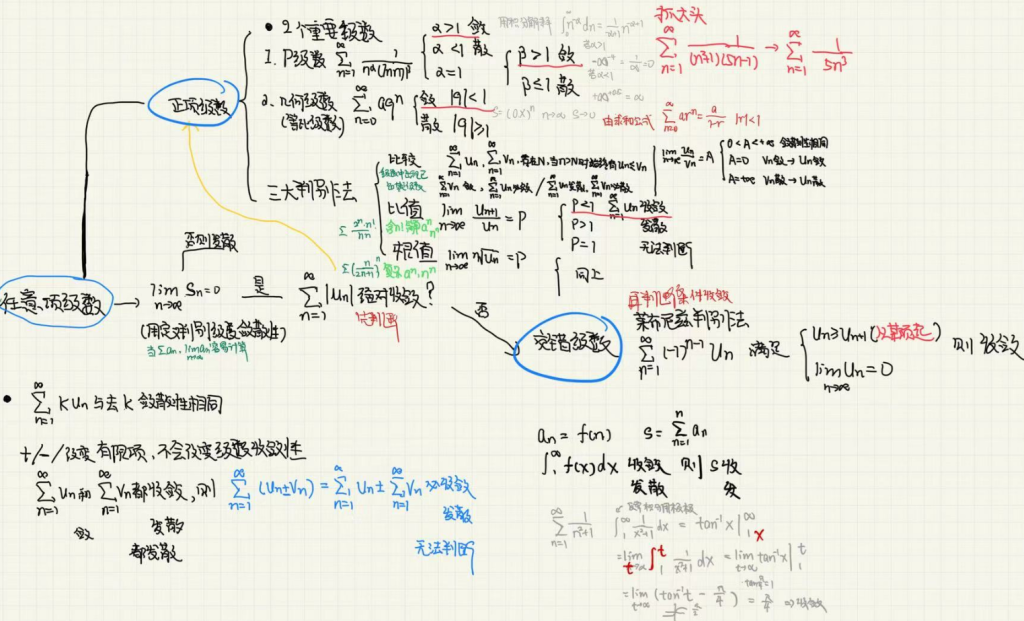
绝对收敛和条件收敛

• 收敛包括绝对收敛和条件收敛，两个在收敛的前提下只有一个成立
• 绝对收敛是更强的条件，所以先判断是否绝对收敛

积分测试只能判断级数的收敛性，不能直接给出级数的和

级数的重排 Rearrangement

指将级数中的项按照不同的顺序重新排列

绝对收敛级数：如果级数\(\sum_{n=1}^{\infty} a_n\) ，绝对收敛，重排不影响收敛性和和

条件收敛级数：如果级数 \(\sum_{n=1}^{\infty} a_n\) 条件收敛（即收敛但不绝对收敛），那么根据 Riemann 重排定理，可以通过适当的重排使其收敛到任意实数，甚至发散到 \(+\infty\) 或 \(-\infty\)。重排可能改变收敛性和和

条件收敛的级数意味着级数的正项和负项分别构成的级数都是发散的。例如，对于级数 \[
\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n},\]正项和负项分别构成的级数\[
\sum_{n=1}^{\infty} \frac{1}{2n-1} \quad \text{和} \quad \sum_{n=1}^{\infty} \frac{-1}{2n}
\]都是发散的。 由于正项和负项都是发散的，我们可以通过调整正项和负项的顺序，来控制级数的部分和。例如，如果我们希望级数收敛到一个较大的正数，可以多取一些正项；如果希望收敛到一个较小的负数，可以多取一些负项

幂级数 power series

形式为：\(\sum_{n=0}^{\infty} c_n x^n = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + \cdots\)

幂级数可能对某些 x 值收敛，对其他 x 值发散，上面的级数类型敛散性与X无关。级数的和是一个函数，上面的级数如果收敛其和为一个数

更一般地，形式为\(2 \sum_{n=0}^{\infty} c_n(x-a)^n = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots\)

称为关于 (x−a)的幂级数或以 a 为中心的幂级数

收敛半径（Radius of Convergence）

对于给定的幂级数 \(\sum_{n=0}^{\infty} c_n (x – a)^n\)，只有三种可能性：

(i) 级数仅在 \(x = a\) 时收敛。

(ii) 级数对所有 \(x\) 收敛。

(iii) 存在一个正数 \(R\)，使得级数在 \(|x – a| < R\) 时收敛，在 \(|x – a| > R\) 时发散。

R 称为幂级数的收敛半径，它描述了该级数在某个区间内收敛，而在该区间外发散

幂级数的收敛区间是级数收敛的所有 x 值组成的区间。在情况 (i) 中，区间仅包含一个点 a。在情况 (ii) 中，区间为 (−∞,∞)在情况 (iii) 中，收敛区间有四种可能性：(a−R,a+R)(a−R,a+R][a−R,a+R)[a−R,a+R]

如何求收敛半径

函数的幂级数表示

将一个已知函数表示为无限多项的和。这种策略对于积分没有初等原函数的函数、求解微分方程以及用多项式逼近函数非常有用

幂级数的微分与积分

幂级数的和是一个函数 \( f(x) = \sum_{n=0}^\infty c_n (x – a)^n \)，其定义域是级数的收敛区间。对用幂级数表示的函数进行微分和积分，等价于对级数中的每一项进行微分或积分，就像我们对多项式积分和求导的操作

尽管定理2说幂级数在微分或积分时收敛半径保持不变，但这并不意味着收敛区间保持不变。可能会发生原始级数在端点收敛，而微分后的级数在该点发散的情况

拿到一个函数，判断对某个级数求N阶导或求积分得到相同的形式，同时对等式右侧的级数和进行相同的操作，下面是对等比级数两侧求导的例子

下面是对已知级数两侧积分的例子

taylor and maclasurin SERIES 泰勒级数与麦克劳林级数

Tyler‘s Formula 泰勒公式 – Skyshin34的博客

在前一节中，我们能够找到某些特定类别函数的幂级数表示。这里我们研究更一般的问题：哪些函数具有幂级数表示？我们如何找到这样的表示？

• 幂级数与泰勒级数的关系：如果一个函数可以表示为幂级数，那么它等于其泰勒级数的和。
• 但有些函数的泰勒级数存在，却不等于函数本身（例如在泰勒级数收敛区间外，或函数在某些点不光滑）

估计级数的和

余项估计公式

当使用积分测试判断级数 \(\sum_{n=1}^{\infty} a_n\) 的收敛性时，如果级数收敛，我们通常想知道级数的部分和 \(s_n = \sum_{k=1}^{n} a_k\) 与级数的总和 \(s = \sum_{k=1}^{\infty} a_k\) 之间的误差 \(R_n = s – s_n\)。这个结论提供了 \(R_n\) 的上下界：

假设 \( f(k) = a_k \)，其中 \( f \) 是 \( x \geq n \) 时的连续、正、递减函数，且 \(\Sigma a_n\) 是收敛的。如果 \( R_n = s – s_n \)，则

$$\int_{n+1}^{\infty} f(x) \, dx \leq R_n \leq \int_{n}^{\infty} f(x) \, dx$$

如果我们将 \( s_n \) 加到不等式的两边得到

$$s_n + \int_{n+1}^{\infty} f(x) \, dx \leq s \leq s_n + \int_{n}^{\infty} f(x) \, dx$$

\(\frac{1}{2n^2}\)是一个常数，与t无关，所以级数通过积分测试

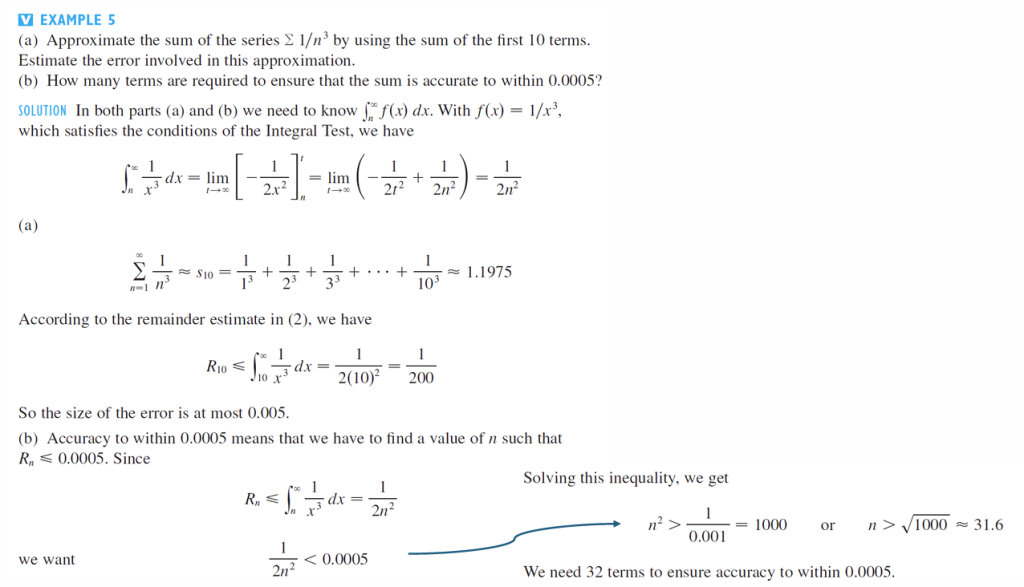
eg1：使用前10项的相变近似函数 \(\sum \frac{1}{n^3}\) 的和，并估计出独立仪中的误差。需要多少项才能确保和精度在0.0005以内？
在(a)和(b)部分，我们都需要知道 \(\int_a^\infty f(x) \, dx\)。对于 \(f(x) = \frac{1}{x^3}\)，它满足积分测法的条件，我们有\[
\int_a^\infty \frac{1}{x^3} \, dx = \lim_{t \to \infty} \left[ -\frac{1}{2x^2} \right]_a^t = \lim_{t \to \infty} \left( -\frac{1}{2t^2} + \frac{1}{2a^2} \right) = \frac{1}{2a^2}
\]\[
\sum_{n=1}^\infty \frac{1}{n^3} \approx s_{10} = \frac{1}{1^3} + \frac{1}{2^3} + \frac{1}{3^3} + \cdots + \frac{1}{10^3} \approx 1.1975
\]根据(2)中的余项估计，我们有\[
R_{10} \leq \int_{10}^\infty \frac{1}{x^3} \, dx = \frac{1}{2(10)^2} = \frac{1}{200}
\]因此，误差的大小最多为0.005。精度在0.0005以内意味着我们需要找到一个 \(n\) 值，使得 \(R_n \leq 0.0005\)。由于\[
R_n \leq \int_n^\infty \frac{1}{x^3} \, dx = \frac{1}{2n^2}
\]解这个不等式，我们得到\[
\frac{1}{2n^2} < 0.0005
\]\[
n^2 > \frac{1}{0.001} = 1000
\]\[
n > \sqrt{1000} \approx 31.6
\]因此，我们需要32项来确保精度在0.0005以内。

eg2：

eg3：交错级数