线性表
栈和队列:操作受限的线性表
串:内容受限的线性表
4.1 串类型的定义

- 子串:一个串中任意个连续字符组成的子序列(含空串),任意串s都是其自身的子串
- 真子串:不包含自身的所有子串
- 空串:零个字符的串。是任意串的子串
- 主串:包含子串的串
- 字符位置:一个字符在序列中的序号
- 子串位置:子串的第一个字符在主串中的位置
- 空格串:由一个或多个空格组成的串,与空串不同
- 串相等:当且仅当两个串的长度相等,并且各对应位置的字符都相等

基本操作中Index(S, T, pos)定位函数的基本思想:
在主串S中取从第i(i的初值为pos)个字符起,长度和串T相等的子串和T比较,若相等,则求得函数值为i,否则i值增1直至串S中不存在和T相等的子串为止
// 函数功能:在字符串S中从pos位置开始查找子串T的位置
int Index(String S, String T, int pos)
{
// 检查pos的有效性(pos需大于0)
if (pos > 0) {
// 获取主串S的长度n,子串T的长度m
n = StrLength(S);
m = StrLength(T);
// i用于记录当前在主串S中匹配的起始位置,初始化为pos
i = pos;
// 循环条件:i的范围需保证子串T能完整匹配(主串剩余长度≥子串长度)
while (i <= n - m + 1) {
// 从主串S的第i个位置开始,截取长度为m的子串sub
SubString(sub, S, i, m);
// 比较截取的子串sub和目标子串T
if (StrCompare(sub, T) != 0)
// 不匹配则i后移一位
++i;
else
// 匹配则返回当前起始位置i
return i;
}
}
// 若未找到匹配或pos无效,返回0
return 0;
}4.2 串的表示和实现
串有3种机内表示方法,分别如下:
定长顺序存储表示
在串的定长顺序存储结构中,按照预定义的大小,为每个定义的串变量分配一个固定长度的存储区
#define MAXSTRLEN 255
typedef unsigned char SString [MAXSTRLEN + 1] //0号单元存放串长度串联接操作和求子串操作见P73
堆分配存储表示
任以一组地址连续的存储单元存放串值字符串序列,但他们的存储空间是在程序执行过程中动态分配而得,空间大小根据串长度动态分配
typedef struct {
char * ch ;
int length ;
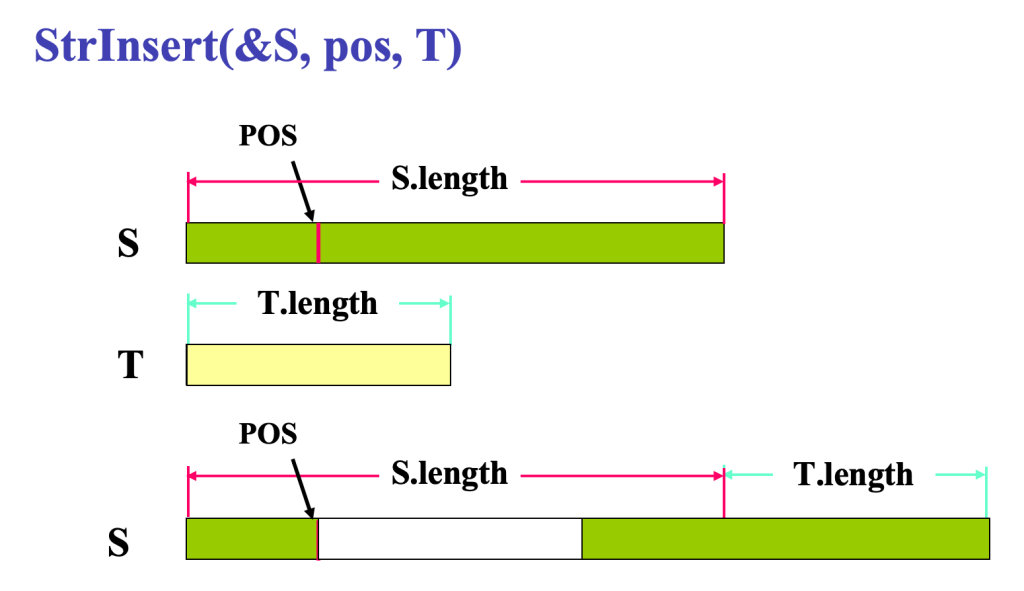
} HString ;串操作:串复制和串插入见P75
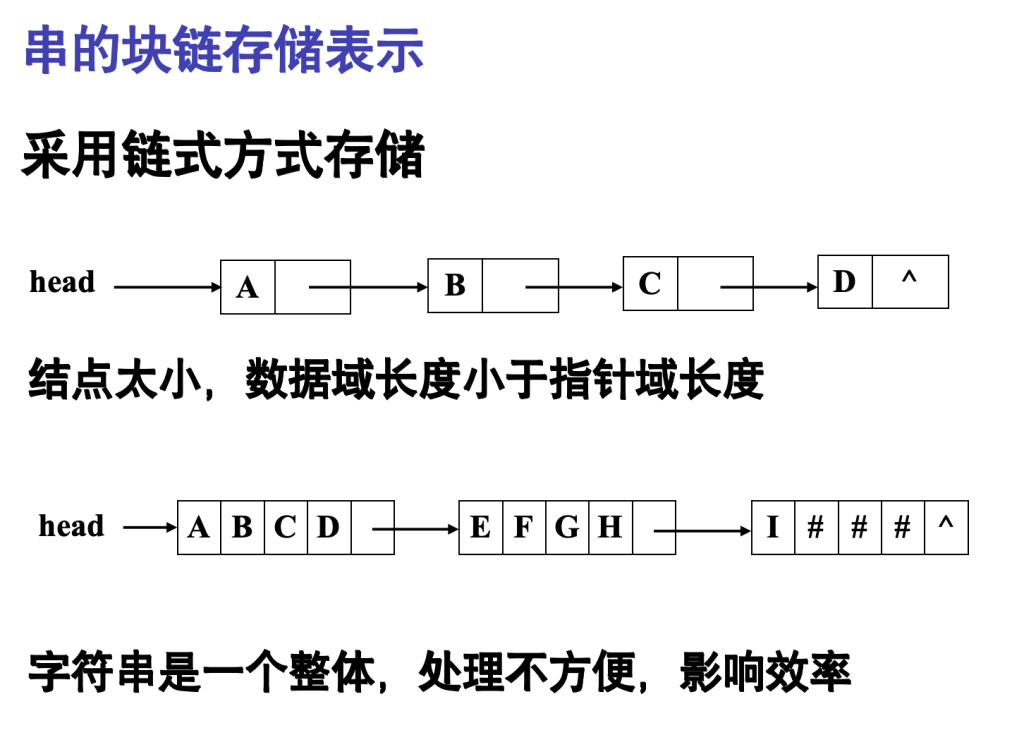
4.2 串的块链存储表示
和线性表的链式存储结构相类似,也可采用链表方式存储值,除头节点外还附设一个尾指针指示链表中最后一个点,虽然对某些串操作比如连接操作有一定方便之处,但总的来说不如另外两种存储结构灵活,它占用存储量大且操作复杂,故在此不讨论。
4.3 串的模式匹配算法
子串的定位操作通常称为串的模式匹配(其中T称为模式串),采用定长顺序存储结构,可以写出不依赖其然串操作的匹配算法:求子串位置的定位函数Index(S, T, pos)
int Index(SString S, SString T, int pos) {
int i = pos; // 主串指针:从pos位置开始匹配
int j = 1; // 子串指针:从子串第1个字符(T[1])开始匹配
// 循环条件:完全遵循原代码 → i <= S[0](主串未遍历完)且 j <= T[0](子串未匹配完)
while (i <= S[0] && j <= T[0]) {
if (S[i] == T[j]) { // 当前字符匹配成功
i++; // 主串指针后移,比较下一个字符
j++; // 子串指针后移,比较下一个字符
} else { // 匹配失败:回溯指针
i = i - j + 2; // 主串回到本次匹配起始位置的下一个位置(原代码公式)
j = 1; // 子串指针重置,重新开始匹配
}
}
// 匹配成功的条件:子串指针j超过子串长度(T[0]),说明子串完全匹配
if (j > T[0]) {
return i - T[0]; // 计算子串在主串的起始位置
} else {
return 0; // 未找到子串,返回0
}
}指针i,j指示主串S和模式串T中当前正待比较的字符位置,从主串Pos的第pos个字符起和模式的第一个字符比较,若相等着继续比较后面的字符,否则从主串的下一个字符起再重新和模的字符比较。以此类推,直至模式T中中的每个字符依次和主串S中的一个连续字符序列相等
算法分析:若S串长度为n,T串长度为m,该算法在指针回较少的情况下,其时间复杂度为O(n+m);若指针回溯较多,最坏情况下其时间将达到O(n*m)。如:
主串 0000000000000000000000000000000000001
模式串 00000001
主要问题:指针回溯
模式匹配的一种改进算法KMP算法
能否设计出一种指针没有回溯的算法?
此算法可以在O(m+n)而不是O(mn)的时间数量级内完成串的模式匹配操作,其改进在于每当一趟匹配过程中出现字符比较不等时,不需要回溯i指针,而是利用已得到的“部分匹配”结果将模式向右尽可能远的一段距离后继续进行比较
我们来看一个例子理解这个算法省略了
回顾图4.3中的匹配过程示例,在第三趟的匹配中,当\( i=7 \)、\( j=5 \)字符比较不等时,又从\( i=4 \)、\( j=1 \)重新开始比较。然后,经仔细观察可发现,在\( i=4 \)和\( j=1 \),\( i=5 \)和\( j=1 \)以及\( i=6 \)和\( j=1 \)这3次比较都是不必进行的。因为从第三趟部分匹配的结果就可得出,主串中第4、5和6个字符必然是‘b’、‘c’和‘a’(即模式串中第2、3和4个字符)。因为模式中的第一个字符是\( a \),因此它无需再和这3个字符进行比较,而仅需将模式向右滑动3个字符的位置继续进行\( i=7 \)、\( j=2 \)时的字符比较即可。同理,在第一趟匹配中出现字符不等时,仅需将模式向右移动两个字符的位置继续进行\( i=3 \)、\( j=1 \)时的字符比较。由此,在整个匹配的过程中,\( i \)指针没有回溯,如图4.4所示。

匹配的后缀可以变成前缀,所以直接开始匹配前缀后一位开始下一轮匹配
假设主串为“s1 s2 s3…sn” 模式串为“p1 p2 p3…pm”为了改进算法,我们需要知道当主串中第i个字符与模式串中j个字符失配时,主串的第i个字符应与模式串中的哪个字符再比较。可以假设此时应与第K个字符比较应该可以跳过多长,这个值由next[j]=k 表示,其表示与j对应的k值即,当模式串中第j个字符与主串中相应字符失配时,在模式中需重新和主串该字符进行比较的位置
int Index_KMP(SString S, SString T, int pos) {
int i = pos; // i 是主串 S 的指针,从 pos 开始
int j = 1; // j 是模式串 T 的指针,从第 1 个字符开始
// 当主串和模式串都还没遍历完时,继续匹配
while (i <= S[0] && j <= T[0]) {
// 情况1:j=0 表示模式串从头开始匹配;情况2:当前字符匹配成功
if (j == 0 || S[i] == T[j]) {
i++; // 主串指针后移
j++; // 模式串指针后移,继续比较下一个字符
} else {
// 字符不匹配,模式串指针 j 跳转到 next[j] 的位置,减少重复比较
j = next[j];
}
}
// 如果 j 超过了模式串的长度,说明匹配成功
if (j > T[0]) {
// 返回主串中 T 的起始位置:i 是主串当前位置,减去模式串长度 T[0]
return i - T[0];
} else {
// 匹配失败,返回 0
return 0;
}
}
//注T[0]表示模式串的长度代码的思路是通过迭代的方式,考试能求出值即可(等待理解),我们用另一种思路计算Next的值
求next函数值的算法:
// 函数名:get_next
// 功能:计算模式串 T 的 next 函数值,并存入数组 next
// 参数:
// - T:输入的模式串(SString 为自定义字符串类型,通常 T[0] 存储字符串长度,T[1..T[0]] 存储实际字符)
// - next:输出数组,用于保存模式串每个位置的 next 值(next[1..T[0]] 有效,next[0] 未使用)
// 核心逻辑:通过前缀后缀的最长公共元素长度,确定字符不匹配时模式串的回溯位置,避免主串指针 i 回溯
void get_next(SString T, int next[]) {
// 初始化变量:
// i:模式串 T 的下标指针(从 1 开始,对应 T[1] 第一个字符)
// j:用于记录前缀的下标,同时表示当前位置前缀后缀的最长公共元素长度
i = 1;
next[1] = 0; // 模式串第 1 个字符(T[1])无前缀,next[1] 固定为 0
j = 0;
// 循环条件:i 未遍历完模式串(T[0] 是字符串长度,i < T[0] 表示未到最后一个字符)
while (i < T[0]) {
// 两种情况进入匹配/更新逻辑:
// 1. j == 0:前缀为空(说明当前无公共前后缀),需重新开始匹配
// 2. T[i] == T[j]:当前模式串的后缀字符(T[i])与前缀字符(T[j])匹配成功
if (j == 0 || T[i] == T[j]) {
++i; // 后缀指针后移,指向 next 要计算的下一个位置
++j; // 前缀指针后移,公共长度 +1
next[i] = j; // 记录当前位置 i 的 next 值:前缀后缀最长公共长度(即 j 的当前值)
}
else {
// 字符不匹配:模式串前缀指针回溯到 next[j] 位置
// 核心:利用已计算的 next 值,跳过无效比较(避免从头开始)
j = next[j];
}
}
}// get_next:函数结束

去掉maxL串中最后一位,在最前面一位加上-1,得到-1 0 0 0 1 2,在每个上加1得到最后的next值0 1 1 1 2 3
也可以这么想,求pj的next值只需要看1到j-1位的子串中重复前后缀的长度 + 1

进一步改进
前面定义的next函数在某些情况下尚有缺陷。例如模式a a a a b在和主串a a a b a a a a b匹配时,当\(i=4\)、\(j=4\)时\(s.ch[4] \neq t.ch[4]\),由\(next[j]\)的指示还需进行\(i=4\)、\(j=3\),\(i=4\)、\(j=2\),\(i=4\)、\(j=1\)这 3 次比较。
实际上,因为模式中第 1、2、3 个字符和第 4 个字符都相等,因此不需要再和主串中第 4 个字符相比较,而可以将模式一气向右滑动 4 个字符的位置直接进行\(i=5\)、\(j=1\)时的字符比较。这就是说,若按上述定义得到\(next[j]=k\),而模式中\(p_j = p_k\),则当主串中字符\(s_i\)和\(p_j\)比较不等时,不需要再和\(p_k\)进行比较,而直接和\(p_{next[k]}\)进行比较,换句话说,此时的\(next[j]\)应和\(next[k]\)相同。由此可得计算next函数修正值的算法如算法 4.8 所示。此时匹配算法不变
void get_nextval(SString T, int nextval[]) {
// 求模式串T的next函数修正值并存入数组nextval。
i = 1; nextval[1] = 0; j = 0;
while (i < T[0]) {
if (j == 0 || T[i] == T[j]) {
++i; ++j;
if (T[i] != T[j]) nextval[i] = j;
else nextval[i] = nextval[j];
}
else j = nextval[j];
}
}// get_nextval
若不相等填入对应的next值,由此得到nextval序列
KMP算法主串的指针不需要回溯的原因
我们已经利用next数组将之前走过的路的有用信息记录下来了
举个例子:假设主串是 A B A B C A B A B D ,模式串是 A B A B D 。
- 当匹配到第 5 个字符(主串是 C ,模式串是 D )时,匹配失败了。
- 这时候, next 数组告诉我们:模式串前 4 个字符 A B A B 里,最长的“前缀=后缀”是 A B (长度 2)
- next[5] = 3,下面说如何推导的
1. 首先要清楚next数组只和模式串有关
2.[5]:匹配到模式串第5个字符时与主串的某字符不匹配
3.“3”:与主串上一轮不匹配的字符进行匹配的模式串的字符的位置,需要找模式串中是否存在重复的元素,由于前一组元素必须从p1即模式串第一个元素开始,所以数值为首尾相同子串长度加 1
本质是:匹配的后缀可以变成前缀,所以直接开始匹配前缀后一位开始下一轮匹配
(但我有一个疑问如果匹配的后缀并不包含最后的元素怎么办:哦我没看定义,定义中要求后缀也必须包含最后的字符,这也是为什么用前后缀描述,因为这个词的意思就是从头开始,从尾开始的含义)
- next[5] = 3,下面说如何推导的
- 所以模式串直接滑到“前缀 A B ”的后面,主串指针 i 不用往回退,继续从 C 后面的字符开始匹配就行
原来的复杂度是O(MN)M为主串长度,N为模式串长度









