词汇

结合律 associative law. 2. 交换律 commutative law. 3. 分配律 distributive law

“Scalar triple product”（标量三重积）是向量运算中一个很重要的概念，广泛用于计算体积和判断向量共面性。a⋅(b×c)

invertible(reversible) 可逆的 irreversible

diagonal entries 对角线元素

upper triangular matrix 上三角矩阵 只有主对角线及以上为非0元素

orthogonal 90度

犯过的错误

不是对称矩阵的行列式等于对角线元素相乘，而是上三角和下三角矩阵

正交矩阵的逆矩阵等于其转置矩阵，不是对称矩阵

向量与平面夹角不能通过平面内随便找一向量来计算，那样除非向量在平面的投影恰好落在该向量上否则结果不对

\[ \sin\theta = \frac{|\vec{a} \cdot \vec{n}|}{\|\vec{a}\| \cdot \|\vec{n}\|} \]

\(\theta\) 是向量 \(\vec{a}\) 与平面的夹角，\(\vec{n}\) 是平面法向量，能这样计算是因为：

\(\theta = \angle(\vec{a}, \text{平面}) = 90^\circ – \angle(\vec{a}, \vec{n})\)
而有恒等式：
\(\sin(\theta) = \cos(90^\circ – \theta)\)

行列式

判断行列式是否为 0，可看是否：

• 存在零行
• 有相同行/列
• 一行是另一行倍数或线性组合

向量积，点积，混合积

叉积没有交换律和结合律，如果交换需要加负号-换方向，只有分配律。点积没有结合律，因为其结果是标量，无法再进行点积，其余所有律都满足

\(\underline{u} \cdot (\underline{v} + \underline{w}) = \underline{u} \cdot \underline{v} + \underline{u} \cdot \underline{w} \ (\text{分配律}) ;\)
\(k(\underline{u} \cdot \underline{v}) = (k\underline{u}) \cdot \underline{v} = \underline{u} \cdot (k\underline{v}) ;\)

\(\underline{u} \times (\underline{v} + \underline{w}) = \underline{u} \times \underline{v} + \underline{u} \times \underline{w} \ (\text{分配律})\)
\((\underline{u} + \underline{v}) \times \underline{w} = \underline{u} \times \underline{w} + \underline{v} \times \underline{w} \ (\text{分配律})\)

Let \(\underline{u} = (3, 1, -4)\), \(\underline{v} = (2, 2, 0)\) and \(\underline{w} = (1, 1, 1)\).

(i) \(\underline{u} \times \underline{v}\),

(v) \(\underline{v} \cdot (\underline{w} \times \underline{u})\),

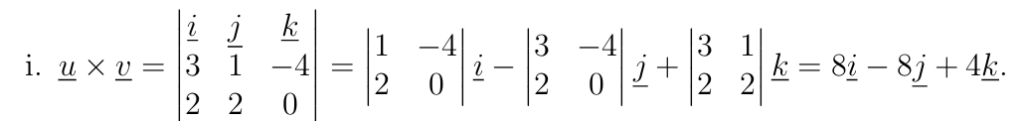
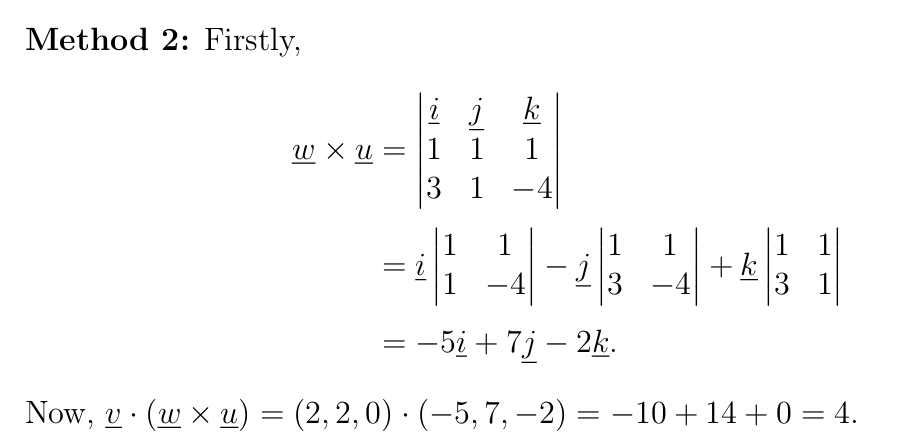
相关题型：给出点坐标通过标量三重积计算立体图形的体积，给出角度利用点积定义计算向量中的参数

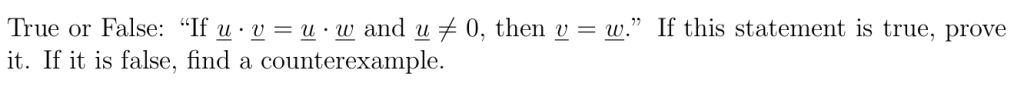
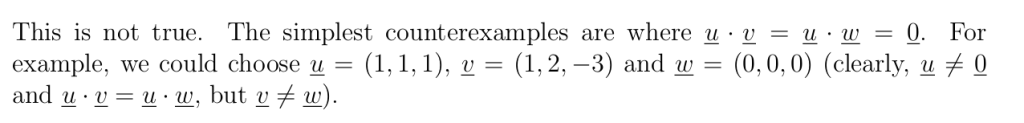
\(w \cdot w = \|w\|^2\)

证明对于所有\(\underline{u},\underline{v} \in \mathbb{R}^n\)，有\(\underline{u} \cdot \underline{v} = \frac{1}{4}\|\underline{u} + \underline{v}\|^2 – \frac{1}{4}\|\underline{u} – \underline{v}\|^2\) 。 [回顾：对于任意向量\(\underline{w}\)，有\(\underline{w} \cdot \underline{w} = \|\underline{w}\|^2\) 。]