Orthogonal Diagonalisation, Symmetric Matrices, and Singular Value Decomposition
内积( dot product )
几何意义:内积 = 向量长度 × 向量长度 × 两向量夹角的余弦值(|x||y|cosθ)。比如两个向量垂直时,夹角 90°,cos90°=0,内积就是 0—— 这是 “正交” 的关键标志。
正交与规范正交基
- 正交向量:两个向量内积为 0(互相垂直),比如
(1,0)和(0,1)。 - 规范正交基:一组向量满足两个条件:① 两两正交(互相垂直);② 每个向量长度都是 1(单位向量)。
例子:3D 空间里,v₁=(0,1,0)(y 轴单位向量)、v₂=(1/√2, 0, 1/√2)(45° 斜向单位向量),再配一个垂直于它们的单位向量,就构成了 3D 空间的规范正交基。
为什么规范正交基好用?
比如要把一个向量u用规范正交基{v₁,v₂,...,vₙ}表示,不用解方程组,直接算 “内积” 就行:u = (u·v₁)v₁ + (u·v₂)v₂ + ... + (u·vₙ)vₙ
类比:就像用直角坐标系表示点,x 坐标就是点到 y 轴的距离,y 坐标就是到 x 轴的距离,直接算就行,不用复杂计算。
正交矩阵:“不改变长度和角度” 的矩阵
正交矩阵是专门和 “规范正交基” 搭配的矩阵,它的核心作用是 “变换后不破坏向量的长度和垂直关系”—— 比如旋转、镜像变换,都能用正交矩阵表示。
怎么判断一个矩阵是正交矩阵?
满足以下任何一个条件都可以(它们是等价的):
- 条件 1:向量经过矩阵变换后,内积不变。比如向量
v和w,变换后Av·Aw = v·w。 - 条件 2:向量经过矩阵变换后,长度不变。比如
|Av| = |v|(旋转不会让向量变长或变短)。 - 条件 3:矩阵的转置等于逆矩阵(
AᵀA = I,A⁻¹ = Aᵀ)。这是计算上最常用的判断方法- 就比如如果矩阵的效果是旋转,从V1方向转到V2方向,转置就是调换坐标轴,相当于矩阵变为从V2到V1的变换,即逆矩阵
- 旋转矩阵一定是正交矩阵,但正交矩阵可以是旋转矩阵也可以是翻转矩阵
旋转矩阵它满足行列式为1,对应平面或空间中的 “纯旋转”(无反射);而正交矩阵的行列式可为1或\(-1\),当行列式为\(-1\)时,正交矩阵包含 “反射” 操作(即翻转矩阵)。
- 条件 4:矩阵的列向量是规范正交基。比如上面的旋转矩阵,列向量
(cosθ, sinθ)和(-sinθ, cosθ)互相垂直、长度都是 1
正交对角化:对称矩阵的 “专属简化方法”
对角化是线性代数的核心目标之一:把复杂矩阵变成对角矩阵(只有对角线有值,其他位置为 0),这样计算(比如求幂、解方程)会特别简单。而 “正交对角化” 是针对 “对称矩阵” 的特殊对角化方法
对称矩阵一定能正交对角化
对 n 阶对称矩阵A,一定存在一个正交矩阵P,让P⁻¹AP = PᵀAP成为对角矩阵(因为P是正交矩阵,P⁻¹=Pᵀ)
这句话的本质是:对称矩阵的特征向量可以构成规范正交基—— 普通矩阵的特征向量可能不垂直,但对称矩阵的特征向量 “天生垂直”(不同特征值对应的特征向量一定正交)
几何理解:P正交矩阵:旋转坐标系,A对角矩阵:伸缩坐标系,P^T正交矩阵的转置即逆矩阵:还原旋转为原来的坐标系
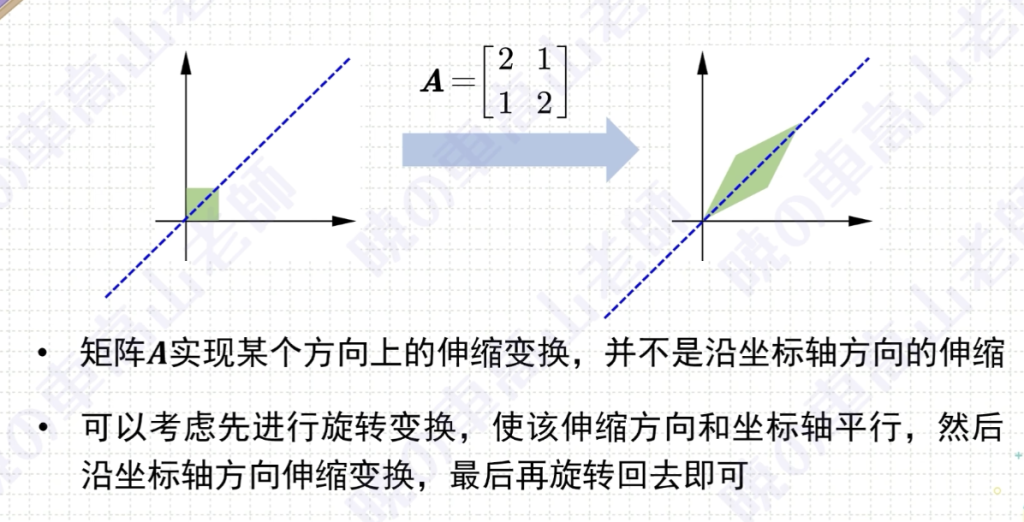
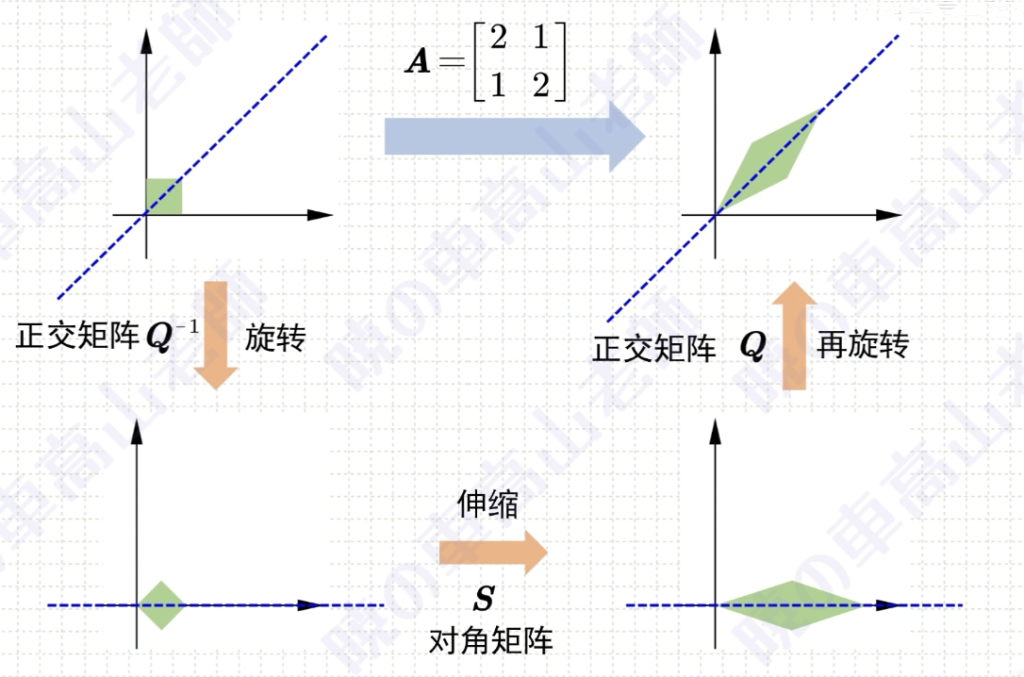
对n阶方阵A,以下条件等价:
(a)A可正交对角化;
(b)A有n个标准正交的特征向量;
(c)A是对称矩阵。
| 对比维度 | 相似对角化(Similar Diagonalization) | 正交对角化(Orthogonal Diagonalization) |
|---|---|---|
| 1. 变换矩阵要求 | 仅需可逆(\(P^{-1}\) 存在) | 必须为正交矩阵 (\(Q^T = Q^{-1}\))要求更严格 |
| 2. 特征向量要求 | 仅需线性无关(P 的列是 A 的线性无关特征向量) | 需单位正交(Q 的列是 A 的标准正交特征向量,即两两正交且模长为 1) |
| 3. 适用矩阵范围 | 所有 “可对角化矩阵”(如:实对称矩阵、有 n 个不同特征值的矩阵、代数重数 = 几何重数的矩阵) | 仅适用于实对称矩阵(实对称矩阵必可正交对角化,且反之,可正交对角化的实矩阵必是对称矩阵) |
| 4. 变换的几何意义 | 一般可逆变换(可能改变向量的长度、夹角) | 正交变换(保持向量的长度、夹角不变,仅旋转 / 反射) |
| 5. 典型应用场景 | 简化矩阵幂运算(如 \(A^k = P\Lambda^k P^{-1}\))、求矩阵行列式(\(|A|=|\Lambda|\)) | 二次型化标准型(消去交叉项且保持几何形状,如解析几何中 “主轴变换”)、PCA(主成分分析)、数据降维 |
对称矩阵
对角线两边的元素 相等。
对称矩阵的转置后和自己一样(因为第X行和第X列的向量相等)
此外,对称矩阵的特征向量互相垂直
对于任何矩阵A,AAT和ATA都是对称矩阵
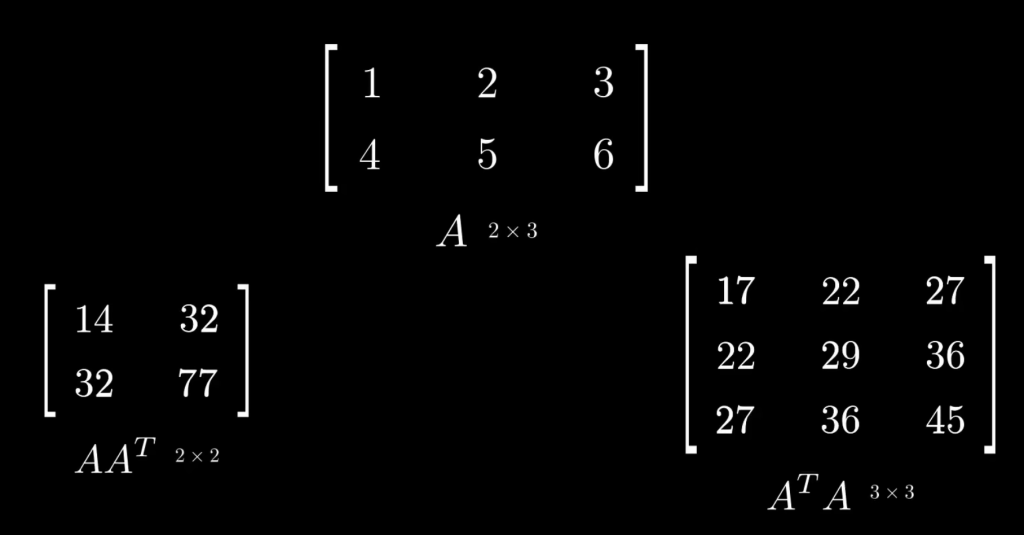
对称矩阵的正交对角化步骤如下:
- 第一步:求A的每个特征子空间的一组基;
- 第二步:对每个特征子空间的基应用格拉姆 – 施密特正交化过程,得到该特征子空间的标准正交基;
- 第三步:将所有特征子空间的标准正交基向量作为列,构成矩阵P,则P是正交矩阵,且可使A对角化(即PTAP为对角矩阵)。

奇异值分解(SVD):“万能矩阵分解法”
正交对角化只适用于 “对称矩阵”,但更多的矩阵是 “非对称矩阵”,甚至不是方阵,
这时候就需要能够分解任何矩阵的方法:“奇异值分解(SVD)
Singular 表示 “某方面独有且突出的特点”,此处对角矩阵表征的是伸缩变换,每个坐标轴方向都有属于自己的独特伸缩因子,因此叫 “奇异值”

对任何 \(m \times n\) 矩阵 A,SVD 都能写成:\(A = U\Sigma V^T\),其中:
- U:\(m \times m\) 正交矩阵(列向量是 “左奇异向量”,按特征值降序排列。对应 A 的列空间和零空间的规范正交基);
- \(\Sigma\):\(m \times n\)“对角矩阵”
只有对角线有值,按降序排序。其他为 0,这些值叫 “奇异值”,奇异值越大,对应部分越重要;- 当矩阵不是方阵时中间的sigma为广义的对角矩阵,形状与原矩阵相同
- \(V^T\):\(n \times n\) 正交矩阵的转置(V 的列向量是 “右奇异向量”,对应 A 的行空间和零空间的规范正交基)。
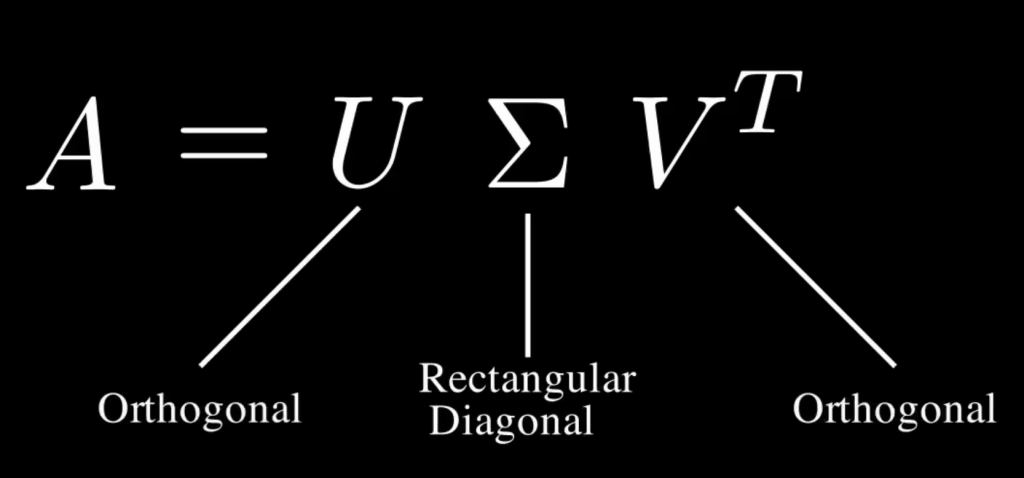
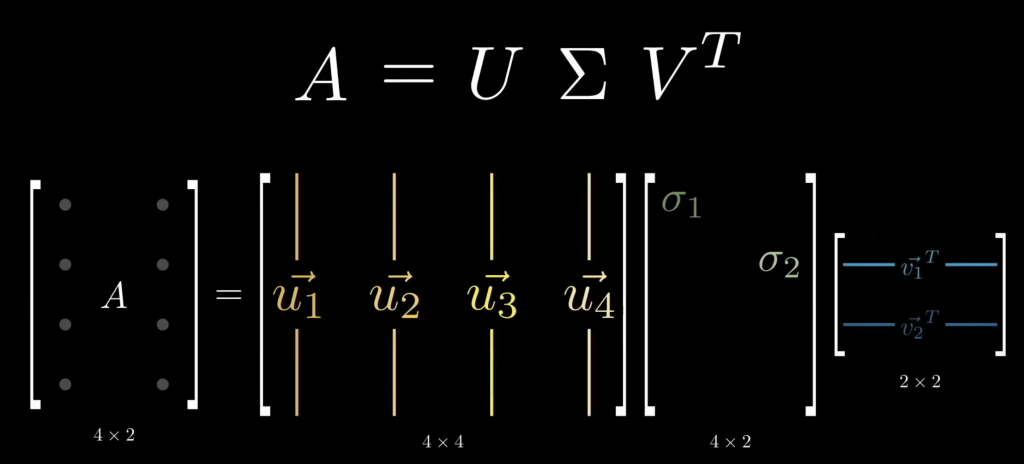
可视化分析
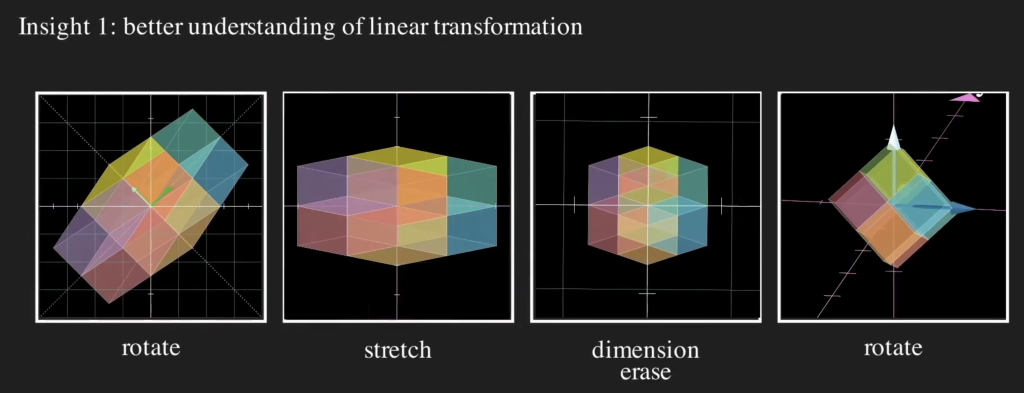
可以把矩阵A的变换拆成 3 步:
- 用
Vᵀ对向量做 “旋转 / 镜像”,保持向量长度不变(因为V是正交矩阵,转置也是正交矩阵); - 用
Σ对对向量进行缩放(只在奇异值对应的方向上缩放,其他方向不变); - 用
U再做一次 “旋转 / 镜像”。
比如图片压缩:奇异值大的部分对应图片的 “主要特征”(比如轮廓),小的部分对应 “细节噪声”,去掉小奇异值,就能在不损失主要信息的前提下压缩图片。
例题说明如何求矩阵的SVD分解

- 注意奇异值在对角矩阵的主对角线要降序排列
若原矩阵不为方阵也是同样的步骤,只要注意U和sigma的形状即可
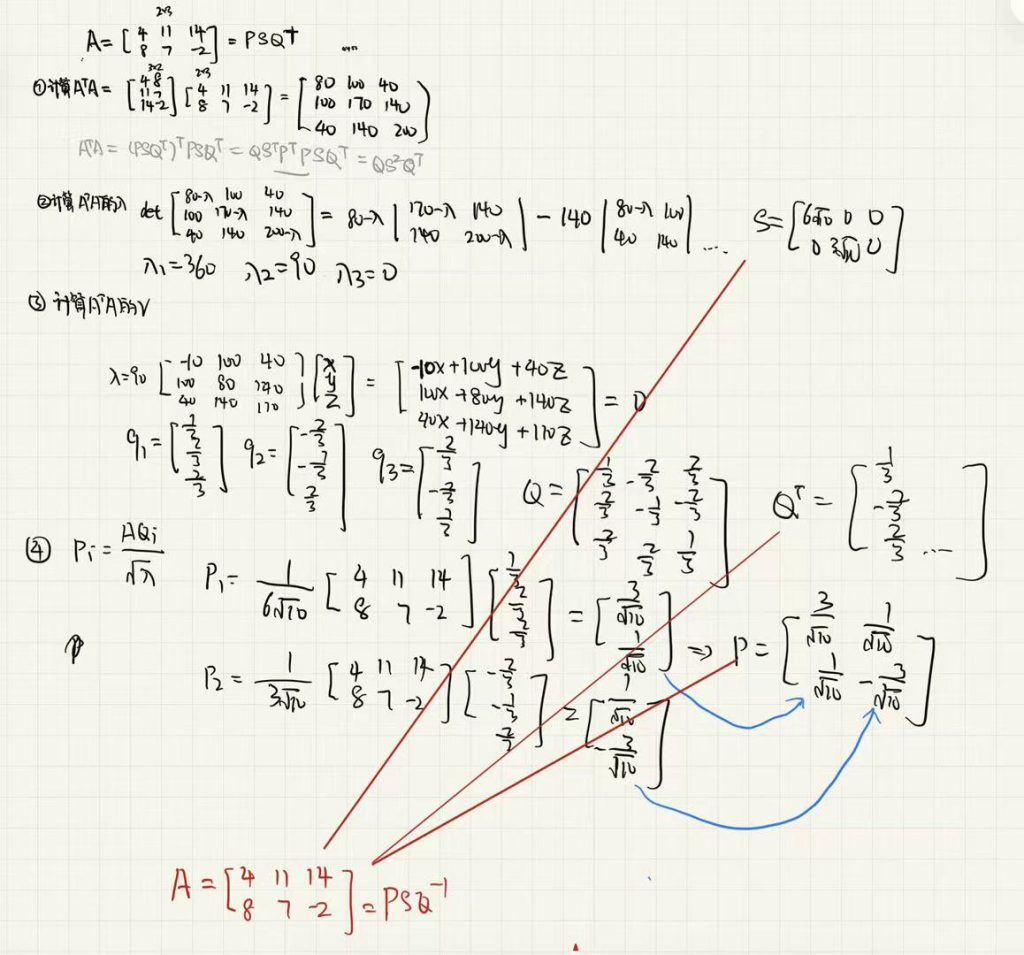
为什么左正交矩阵要通过右正交矩阵乘以原矩阵 / 奇异值计算

为什么要求A A^T的特征值和向量,化成这个形式的原因是因为一个矩阵乘以自己的转置一定是对称矩阵,对称矩阵的一个特性是其特征向量一定是互相垂直的,这样我们只需要对特征向量单位化就能保证用特征向量构建的矩阵是正交矩阵


对于奇异值(特征值)为0时如何在最后用求U矩阵


复数与复矩阵的对角化
实数矩阵可能没有实数特征值,但复数矩阵一定有特征值(因为复数多项式能完全分解成一次因式)。
比如 n 阶复数矩阵,不管 n 是多少,至少有一个复数特征值;如果 n 是奇数,实数矩阵也一定有一个实数特征值(因为复数特征值是成对出现的,奇数个特征值里必然有一个实数)。
矩阵代数的应用:矩阵差分方程与微分方程
其中\(y = f(x)\)是待求的未知函数,\(y’ = \frac{dy}{dx}\)是y对x的导数,a是常数。方程(3)的通解为\(y = ce^{ax}\)(\(c \in \mathbb{R}\),e为自然常数),即有无穷多个解。在实际物理问题中,通常会给出 “初始条件” 来确定唯一解。例如,若要求解满足\(y(0) = 3\),则代入通解得\(3 = ce^{0}\),即\(c = 3\),唯一解为\(y = 3e^{ax}\)。
本节关注线性微分方程组的求解,这类方程组的一般形式为:\(\begin{cases} y_1′ = a_{11}y_1 + \cdots + a_{1n}y_n \\ y_2′ = a_{21}y_1 + \cdots + a_{2n}y_n \\ \vdots \\ y_n’ = a_{n1}y_1 + \cdots + a_{nn}y_n \end{cases}\)
其中\(y_1, \cdots, y_n\)是待求的未知函数,\(a_{ij}\)(\(i, j = 1, \cdots, n\))是常数。用矩阵表示,上述方程可简写为:\(\begin{pmatrix} y_1′ \\ \vdots \\ y_n’ \end{pmatrix} = A \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix}\)
其中\(A = (a_{ij})\)是n阶常数矩阵。若A是对角矩阵,求解这类方程组只需分别求解每个一元微分方程,是上述简单微分方程的直接推广。
例 :设\(A = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 5 \end{pmatrix}\)(3 阶对角矩阵),则对应的微分方程组为:\(\begin{cases} y_1′ = 2y_1 \\ y_2′ = 3y_2 \\ y_3′ = 5y_3 \end{cases}\)
由一元微分方程的通解公式,方程组的通解为:
\(y_1 = c_1e^{2x}\),\(y_2 = c_2e^{3x}\),\(y_3 = c_3e^{5x}\)
其中\(c_1, c_2, c_3 \in \mathbb{R}\)是任意常数。
我们要解的是Y′=AY(其中A是系数矩阵)。如果A是对角矩阵,比如A=(a00b),那么方程组会被拆成两个独立的一元微分方程:
{y1′=ay1y2′=by2
这时候我们能直接用 “y′=ky的通解是y=cekx” 来求解,非常简单。
但如果A不是对角矩阵,我们需要变量替换,构造一个新的变量U,让新的方程组U′=ΔU(Δ是对角矩阵),这样就能用对角矩阵的简单解法来处理了,最后再通过我们所设的Y = PU变换将U变为Y就能得到原解了










