
霍纳法则(horner’s rule)—计算多项式值的高效算法
对于多项式求值问题,我们最容易想到的算法是求出每一项的值然后把所求的值累加起来,这种算法的时间和空间效率都不高。霍纳法则通过将多项式重新分解为嵌套的线性形式,减少计算复杂度。



其实上面的题主最后并没有给出这种方法可以简化多项式计算的的理由,其实是将高次幂转化为连续的线性乘法,从而避免直接计算高次幂,从而减少了一层循环
Legendre basis 勒让德多项式

是一组在数学和物理学中非常重要的正交多项式,它们的递推关系提供了一种高效的计算方法,可以避免直接求解微分方程或积分表达式。
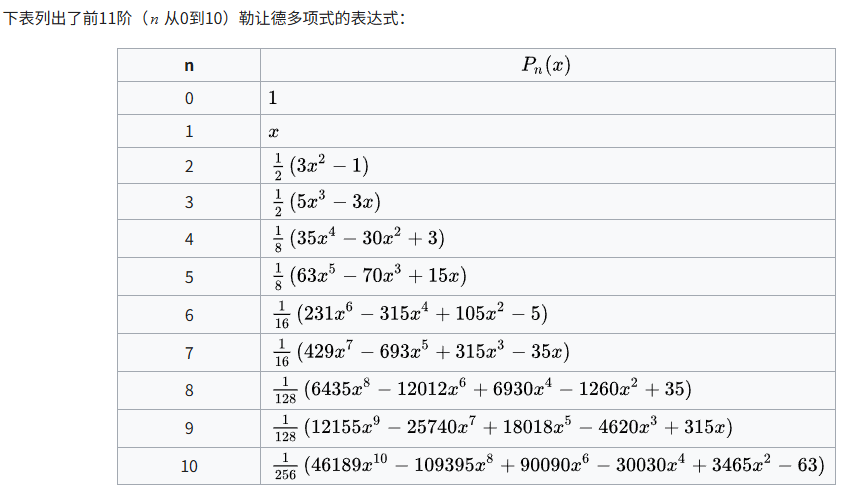
切比雪夫多项式到单项式(Chebyshev to Monomials)
推导多项式的递推公式:
棣莫弗定理 复数 – Skyshin34的博客
二项式定理:
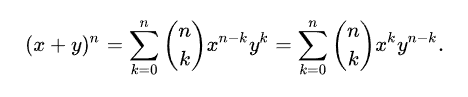


递推公式:
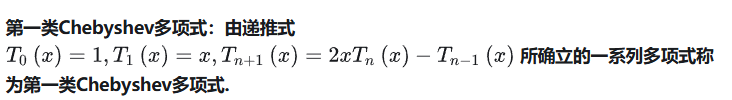
自变量为三角函数时的性质,在[-1,1]时的另一种表示
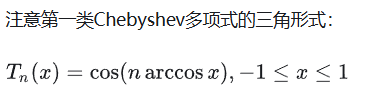

带权正交性
第一类切比雪夫多项式在区间 \([-1, 1]\)上关于权函数 \(\frac{1}{\sqrt{1 – x^2}}\) 具有正交性

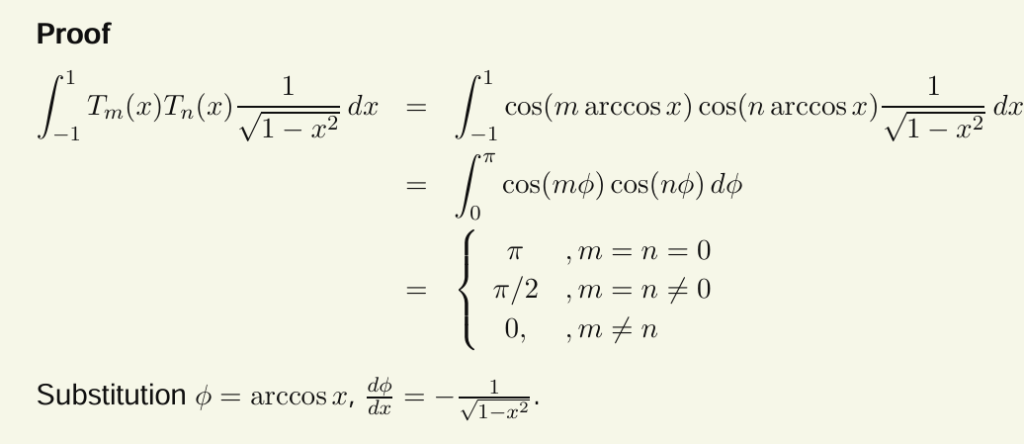
普通多项式转切比雪夫多项式


多项式表示切比雪夫多项式的递推公式


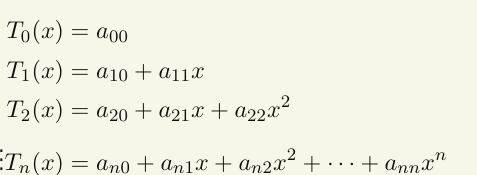
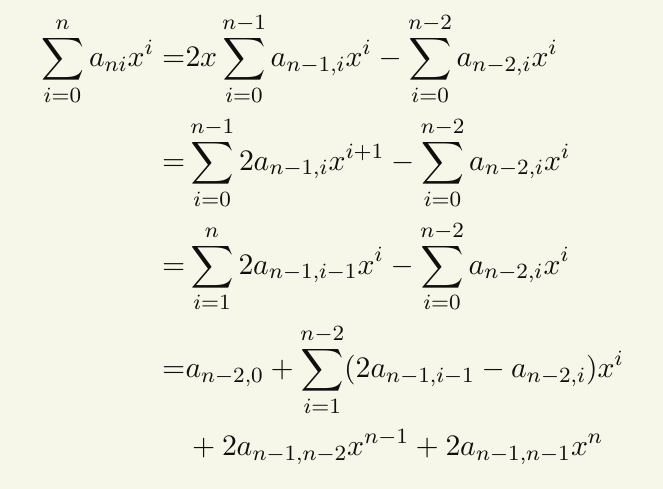
将最终结果一一对应可以得到
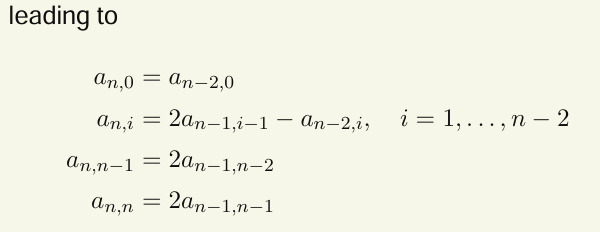
生成函数
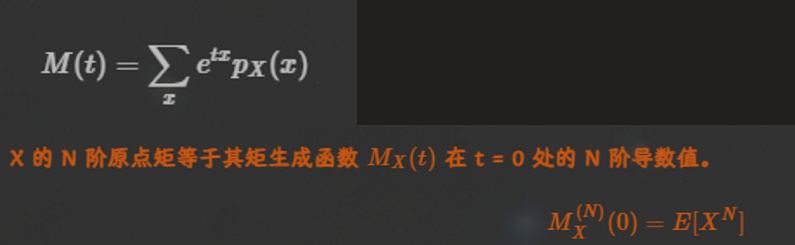
类比之前学习的矩生成函数,可以发现都同样有着形式变量,需要看求导的系数。通过生成函数可以获得任意阶切比雪夫多项式

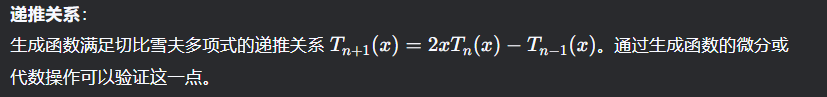
显式表达式


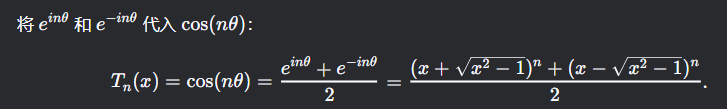
对称性
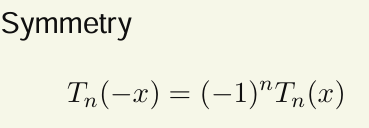

零点和极值点
证明思路:
求\(T_{n}\left(x_{k}\right) = 0 \)的根,利用切比雪夫多项式的三角定义\(T_{n}(\cos \theta)\) = \(\cos (n \theta) \),则要求\( \cos \left(n \theta_{k}\right) = 0 \)。解得 \(n \theta_{k} = \pi(k+1 / 2)\) ,即\( \theta_{k} = \frac{\pi(k+1 / 2)}{n} \)
当\(\theta = \frac{\pi}{2n}, \frac{3\pi}{2n}, \ldots, \frac{(2k-1)\pi}{2n}, \ldots, \pi \)时,\( \cos(n\theta) = 0 \)
\( T_n(x) \) 在 \([-1,1]\) 中有 \( n \) 个单根,分别为
\[ x_k = \cos\left(\frac{2k-1}{2n}\pi\right), \quad k=1,2,\ldots,n \]
同理,当\( \theta = 0, \frac{\pi}{n}, \frac{2\pi}{n}, \ldots, \frac{k\pi}{n}, \ldots, \pi \)时,\( \cos(n\theta) = 1, -1, 1, -1, \ldots, (-1)^n \)
\( T_n(x) \) 在 \([-1,1]\) 中有 \( n+1 \) 个极值点,为 \( x_k = \cos\left(\frac{k}{n}\pi\right), \quad k=0,1,\ldots,n \)且对于每个极值点,其极值为 \( T_n(x_k) = (-1)^k \)

看不太懂但将来可能要用的性质

Reference:









