Reference:
前置知识
矩阵三种初等行变换和高斯消元对应关系
① 给某行同时乘以一个非零常数k \(\leftrightarrow\) 某方程约去系数公因数
② 交换某两行的位置 \(\leftrightarrow\) 交换方程组内的两个方程
③ 把某一行的k倍加到另一行上 \(\leftrightarrow\) 方程组的加减消元
线性方程组解的判定
\[A\vec{x}=\vec{b}\]若无解,当且仅当:系数矩阵的秩数 < 增广矩阵的秩数

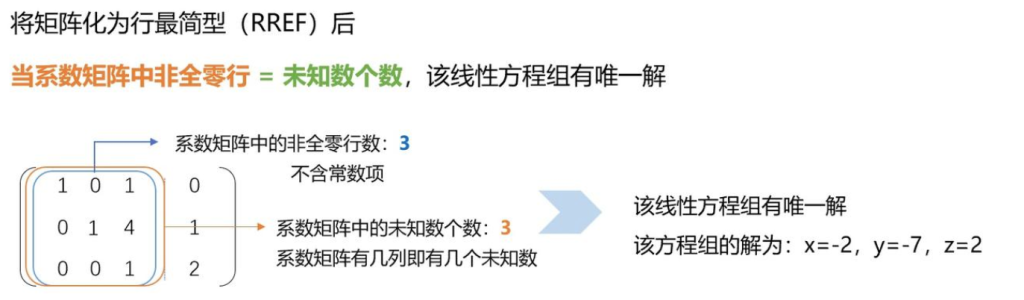
\[A\vec{x}=\vec{b}\]有唯一解当且仅当:系数矩阵的秩数 = 未知数个数
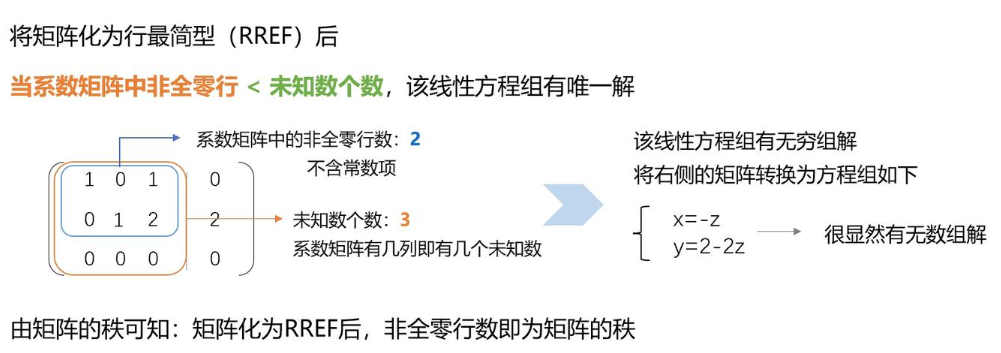
\[A\vec{x}=\vec{b}\]有无穷多组解当且仅当:系数矩阵的秩数 < 未知数个数


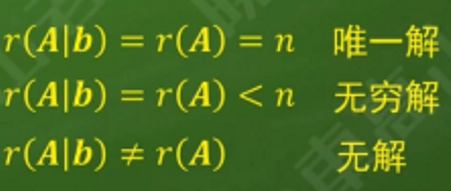
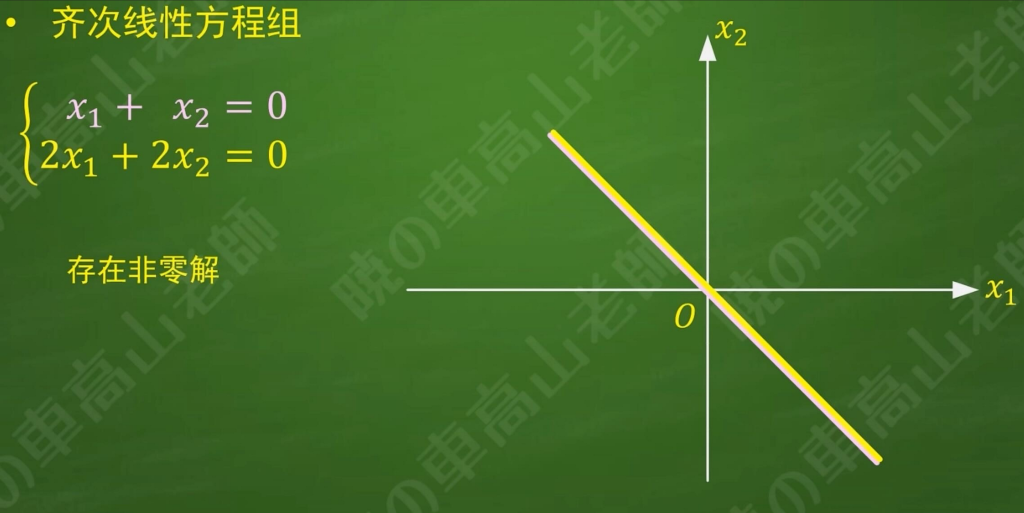
齐次线性方程组解的判定
齐次线性方程组,因为等号右边全为零,所以不会存在无解的情况
至少存在一组全零解,使得等式成立
所以齐次线性方程组的解只有两种情况:
① 有唯一解(系数矩阵的秩数 = 未知数个数),即为零解
② 有无穷多组解(系数矩阵的秩数 < 未知数个数),即为无穷多组解
那齐次线性方程组的无穷多组解,该如何表示出来呢?
答案是:用基础解系来表达这无穷多组解
基础解系(极大线性无关组)
指在无穷多组解中,找到一组解,且满足:
① 这组解内的向量线性无关
② 方程组的任意一个解都可由这组向量线性表示
那么这组解(向量组),就称为基础解系
这和极大线性无关组是一回事
基础解系到通解
通解就是线性方程组解的具体表达方式有了基础解系(一组线性无关的列向量)
那么每个列向量×对应系数再相加即为该方程组的通解,对应系数可为任意常数
求解齐次线性方程组的基础解系和通解
总览:
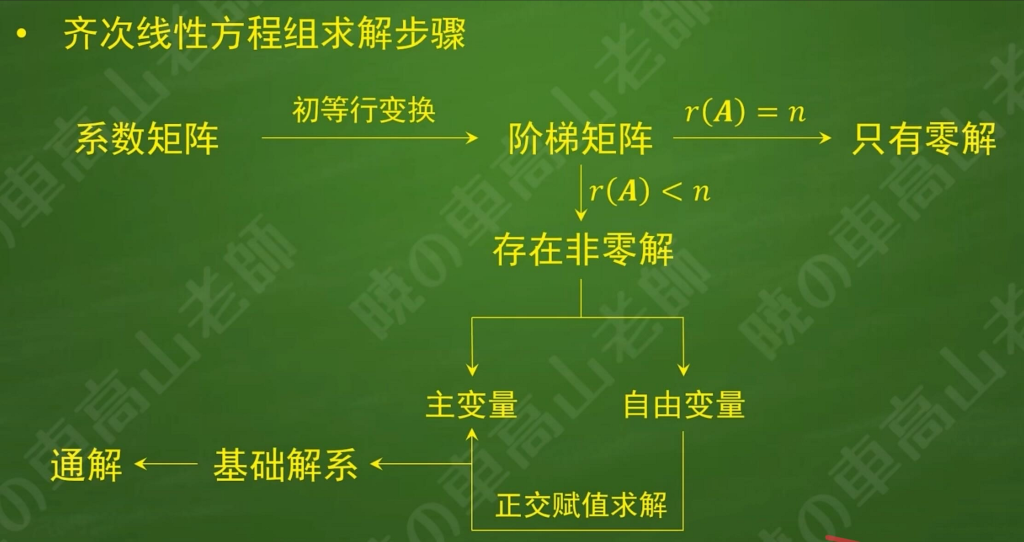

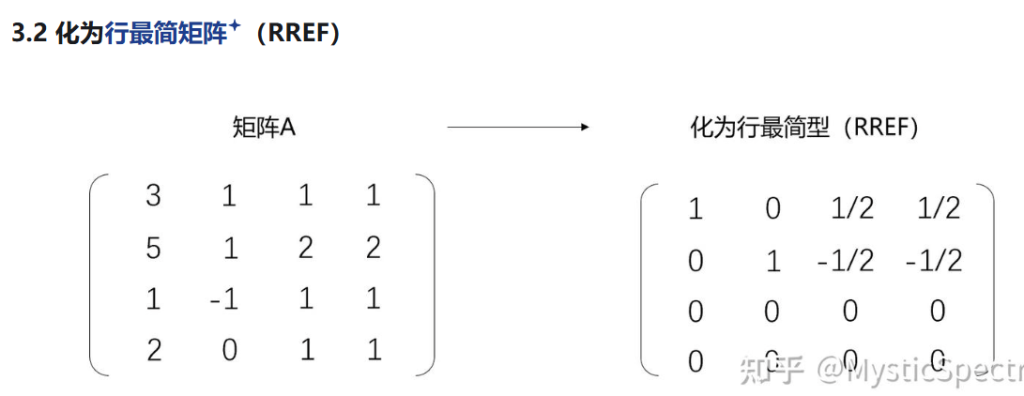
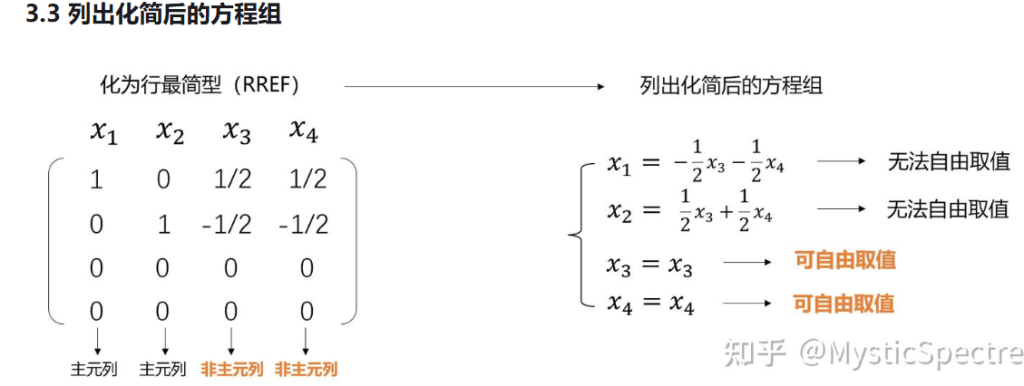
在处理线性方程组相关问题时,重点不是把自由变量(比如这里说的类似 \(x_1\)、\(x_2\) 这类自由变量)进行正交赋值后带回方程去解主变量,而是去寻找 “变换率”。具体来说,是用自由变量来表示其他变量,然后提取出表示这种关系的系数,这些系数就体现了变量之间的变化率。之前可能错误地认为需要把自由变量赋值后带回方程去解方程求主变量,但实际更关键的是通过用自由变量表示其他变量,得到变量间的变化规律(即变化率相关的系数关系)

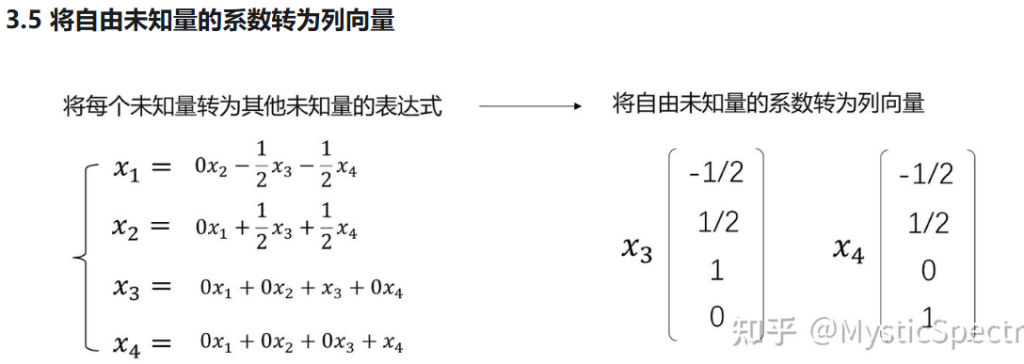



解的情况

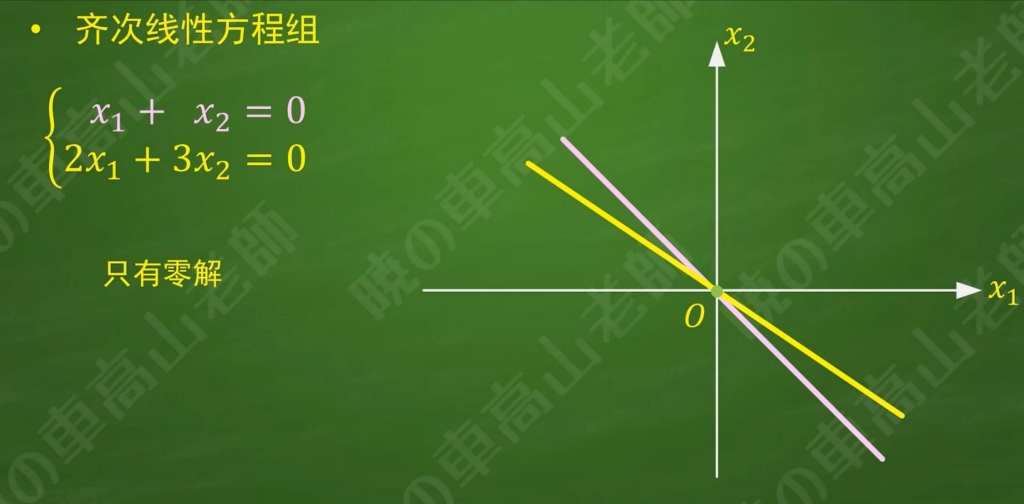
非齐次线性方程组
非齐次线性方程组的通解由齐次的通解和非齐次的特解组成
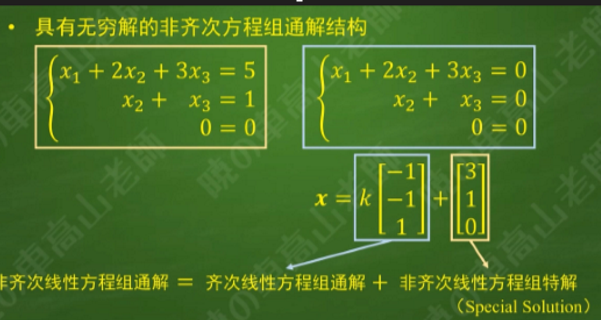
在阶梯增广矩阵中令全体自由变量为0即可得到特解。

自由变量呢,就像是小组里最 “自由” 的那个成员,它不用被其他成员的 “规则” 死死限制,能自己选值
梯形化后该行非主元列的未知量 – 人话,不是每一行的第一列非0元素,起码得是第二列非0元素








