本文最后更新于231 天前,其中的信息可能已经过时,如有错误请留言


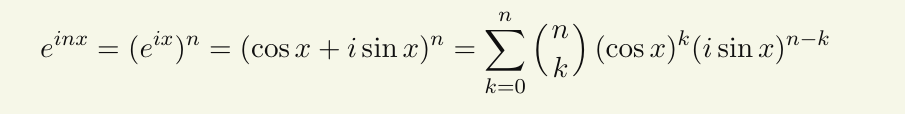

i的几何意义

至此我们赋予i在复平面单位圆中几何意义:不改变复数所代表的向量模长并逆时针旋转90°
推导(不是证明)
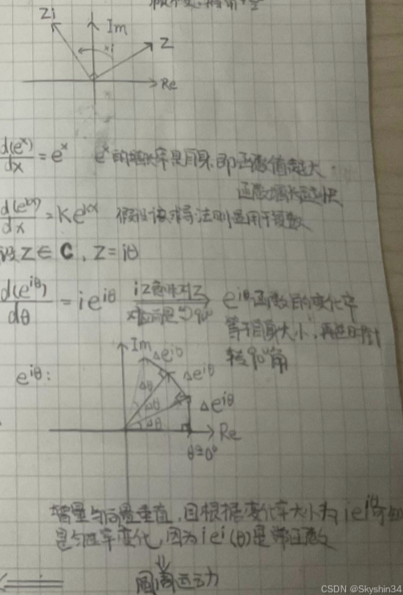
重点:\( e^{i\theta} \),该函数的随自变量变化的图像就是复平面的单位圆,是周期函数。而复平面单位圆可以用极坐标表示,两者联立起来,便可以得到欧拉公式
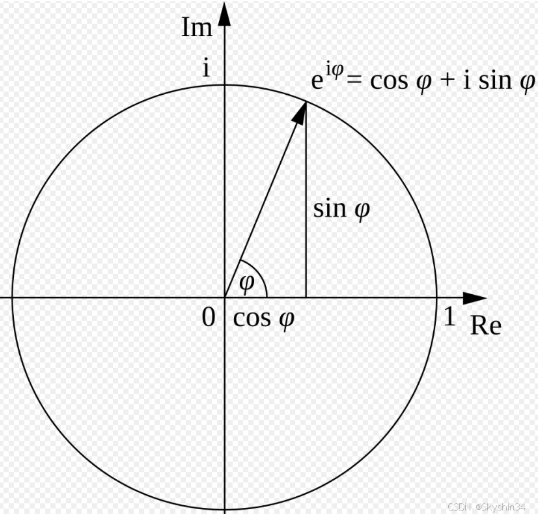

泰勒展开证明欧拉公式

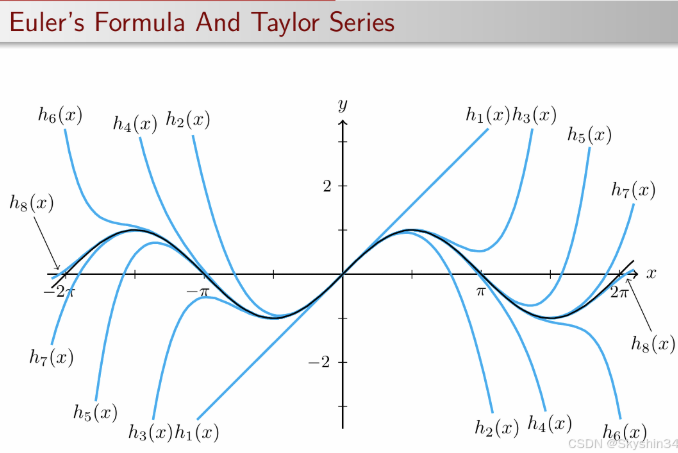
例题
定义->极坐标复数,通过欧拉公式转化为Exponenial指数复数

欧拉形式的复数转化为极坐标->定义复数

Hyperbolic and trigonometric functions 双曲和三角函数


Osborne’s Rule(奥斯本法则)










