Reference:如何简单理解概率分布函数和概率密度函数?_概率密度函数和分布函数的关系-CSDN博客https://blog.csdn.net/ypp0229/article/details/104982664
离散型随机变量和连续型随机变量
离散型随机变量是指其数值只能用自然数或整数单位计算的则为离散变量。例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得。反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值。例如,生产零件的规格尺寸,人体测量的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得
离散型随机变量的概率函数 – 概率质量函数 PM(mass)F
连续随机变量的概率函数 – 概率密度函数 PD(density)F
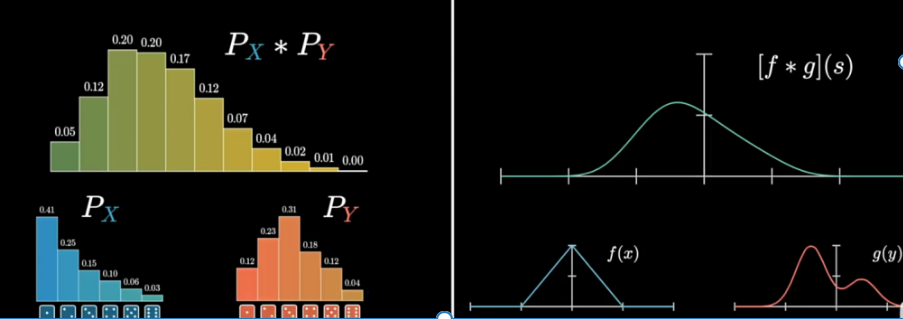
与下面的连续随机变量的概率密度函数(PDF)不同,PMF直接给出了随机变量取某个值的概率。

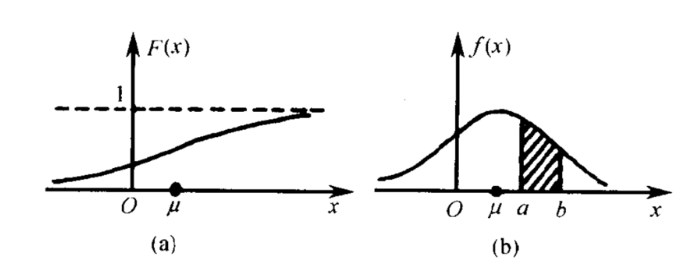
左边是F(x)连续型随机变量分布函数画出的图形,右边是f(x)连续型随机变量的概率密度函数画出的图像
连续型随机变量的“概率函数”换了一个名字,叫做“概率密度函数”,对累积分布函数(CDF)求导可以得到概率密度函数(PDF)。两张图一对比,你就会发现,如果用右图中的面积来表示概率,利用图形就能很清楚的看出,哪些取值的概率更大!所以,我们在表示连续型随机变量的概率时,用f(x)概率密度函数来表示,是非常好的!
定义为\( F_X(x) = \int_{-\infty}^{x} f_X(t) \, dt \),则 \( X \) 是一个连续型随机变量,并且 \( f_X(x) \) 是它的概率密度函数
概率质量函数 Vs. 概率密度函数
在概率论中,概率质量函数(probability mass function,简写为pmf)是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数不同之处在于:概率质量函数是对离散随机变量定义的,本身代表该值的概率;概率密度函数是对连续随机变量定义的,本身不是概率,只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。
离散型随机变量的概率分布
这样的列表都被叫做离散型随机变量的“概率分布”。严格来说,它应该叫离散型随机变量的值分布和值的概率分布列表”,这个名字虽然比“概率分布”长了点,但是肯定好理解了很多。因为这个列表,上面是值,下面是这个取值相应取到的概率,而且这个列表把所有可能出现的情况全部都列出来了!

离散/连续随机变量的(概率)分布函数 – 累积概率函数 CDF Cumulative Distribution Function
设离散型随机变量X的分布律是
\[ P \{ X = x_k \} = p_k \quad k=1,2,3\cdots \]
则\[ F(x) = P(X \leq x) = \sum_{x_k \leq x} p_k \]F(x)就代表概率分布函数啦。即F(x)=P(X<x) (-∞<x<+∞)。这个符号的右边是一个长的很像概率函数的公式,但是其中的等号变成了小于等于号的公式。它就是概率函数取值的累加结果!所以它又叫累积概率函数!研究一个随机变量X取值小于某一数值x的概率,这概率是x的函数,称这种函数为随机变量ξ的分布函数简称分布函数
概率函数和概率分布函数就像是一个硬币的两面,它们都只是描述概率的不同手段!
于是连续型随机变量X的概率分布函数可写为常用的概率积分公式的形式:
\[F(x) = \int_{-\infty}^{x} f(x) \, dx.\]
例题
例1:

- 当等比数列项数无穷时的求和公式不同
- PMF和CDF计算P(X<= x)的方式不同,PMF是一个一个代入X后求和,CDF是直接代入公式X的临界值
例2:计算E(XY),验证XY是否独立的方法

- 列表计算F(XY),不能从F(x)和F(Y)直接得出
- 验证独立性时要带入具体值,后来我想想是废话,之前不带入是因为有P(XY)和P(x)的通式,现在没有通式取一个值验证即可
例3:

遇到证明题,尽量写出定义式,就能破局
例4:


第一句话中的first翻译为前,而不是第一次。求前\(n – 1\)次抛掷都为反面的概率
第二、三句话中的first翻译为第一次,第一次正面出现在第n次抛掷的概率是多少?设X为记录首次出现正面的抛掷次数的随机变量
做了一个变量替换

例5:二项分布

例6:不能用排列组合数计算总数的情况 – 不同事件有相同元素
排列组合数不包括不同项相同的组合,所以当题目中比如骰子这种两次都可以相同且顺序很重要的题型,用乘法公式/枚举,这题36是通过符合条件的数量/总数量计算的(如果通过排列数需要+6个相同的项总数才正确),分子是通过列举(1,1~6) (2~6,1) = 6+5项得到的,这就是答案的解法

我的错误:试图通过A62计算分母的组合总数,但这样就会忽略两次抛数相同的情况
所以如果题目不同事件可以拥有相同的值的情况下,用乘法公式而不是排列组合数计算事件的数量 和 事件总数,通过满足事件的数量 / 事件总数计算概率,而不是像经典分布用
满足条件事件1 × 事件对应的概率 + 满足条件事件2 × 事件对应的概率…计算
例7:牌的数字和牌本身要独立,如何计算Z=X+Y
不要被数字迷惑,即使数字相同,但是是不同牌
所以这个不是硬币的值相同问题,不能拿相同的牌(不放回),先拿A牌和先拿B牌是同一种情况(我的理解是本题没有强调拿取顺序不同,所以就不考虑顺序),可以用组合数计算总数
回顾:这题不但可以有相同元素,甚至相同元素交换顺序都算2种不同情况,所以用排列组合肯定会少算情况

我的错误:我以为(1,2)(2,1)(1,1)(1,1)是一种情况,所以概率质量函数的分母我写的是5
例8:又忘记在符合条件的组合数的概率前乘符合条件的组合数了,做题前先审视是特殊分布与否?