方向角与方向余弦
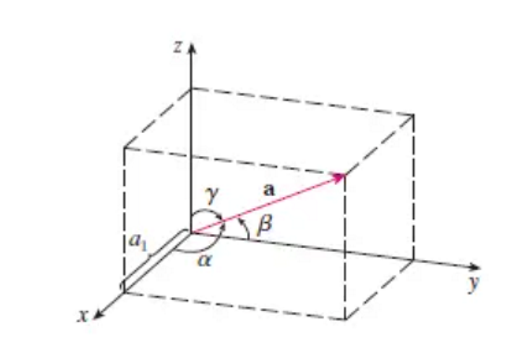
非零向量 \(\mathbf{a}\) 与三条坐标轴正向的夹角 \(\alpha, \beta, \gamma\) 称为向量 \(\mathbf{a}\) 的方向角,设向量 \(\mathbf{a} = (x, y, z)\),方向角的余弦值\(\cos\alpha, \cos\beta, \cos\gamma\) 称为向量a的方向余弦(| a |的算法见上单位向量)
\[
\cos\alpha = \frac{x}{|\mathbf{a}|}, \quad \cos\beta = \frac{y}{|\mathbf{a}|}, \quad \cos\gamma = \frac{z}{|\mathbf{a}|}
\]
单位(方向)向量u
定义:模长为1的任意方向向量
所以第一种计算方式为:方向向量(任取直线两点坐标做差) / 向量的模
向量各分量的平方和的算术平方根是它的模(L2范数),即有 \(|\mathbf{u}| = \sqrt{u_1^2 + u_2^2 + u_3^2 + \ldots + u_n^2} = 1\)
以向量a的方向余弦为坐标的向量就是与 a同方向的单位向量 \(\mathbf{e}_a\)
证明\[
(\cos\alpha, \cos\beta, \cos\gamma) = \left(\frac{x}{|\mathbf{a}|}, \frac{y}{|\mathbf{a}|}, \frac{z}{|\mathbf{a}|}\right) = \frac{1}{|\mathbf{a}|}(x, y, z) = \frac{\mathbf{a}}{|\mathbf{a}|} = \mathbf{e}_a,
\]
单位向量可以表示为方向余弦的向量,而单位向量的L2范数等于1,所以可得:
\[
\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1
\]
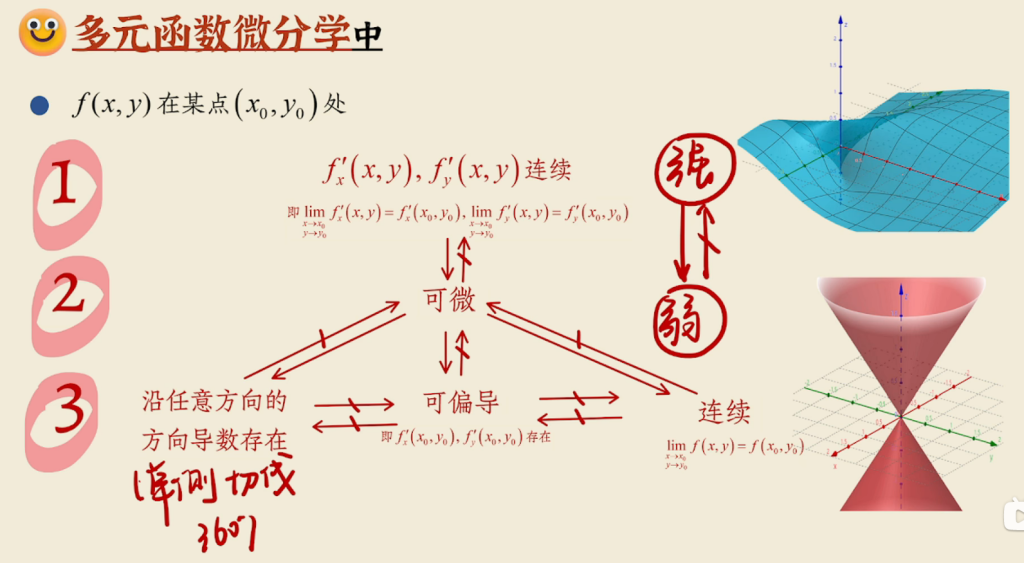
方向导数
定义
导数:反映的是函数y=f(x)在某一点处沿x轴正方向的变化率
偏导数:偏导数也就是函数在某一点上沿坐标轴正方向的的变化率,所以偏导数的方向不是切线方向,而是沿着自变量坐标轴的方向
方向导数:偏导数只看两个方向,即从点两侧沿坐标轴的方向,而方向导数就是函数在任意方向上的变化率。可以说偏导数是方向导数的特例。所以从定义如下

如果 \(f(x, y)\) 是 x 和 y 的函数,且 \(u = u_{1}i + u_{2}j\) 是单位向量,则 f 在点 \((x_{0}, y_{0})\) 处沿 u 方向的方向导数记为 \(D_{u}f(x_{0}, y_{0})\),定义为(实际不通过这种方式计算方向导数)
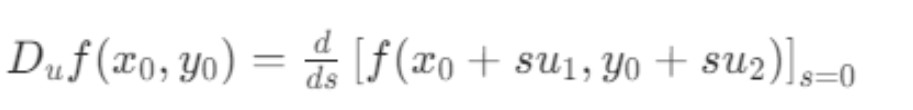
\(D_{u}f(x_{0}, y_{0})\) 可以解释为曲面 \(z = f(x, y)\) 在点 \((x_{0}, y_{0}, f(x_{0}, y_{0}))\) 处沿 u 方向的斜率。方向导数表示 \(f(x, y)\) 在点 \((x_{0}, y_{0})\) 处沿 u 方向关于距离的瞬时变化率。
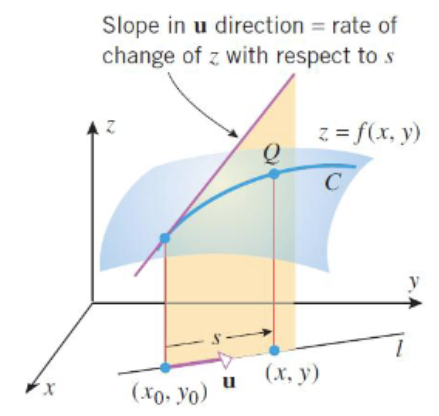
可进一步将方向导数的定义式写成以下形式:
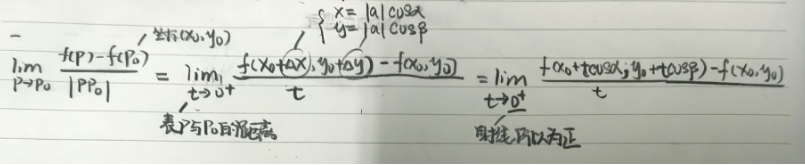

例题:

此外,偏导数是双侧极限,方向导数是单侧极限,通过下面一个例子理解

在(0,0)对X轴的偏导不存在(不光滑),对X轴正方向的方向导数存在为1
计算公式
但实际计算中并不通过定义求方向导数,通过下公式计算(方向导数 = 梯度 点乘 单位向量)

证明:

例题:


梯度
公式:
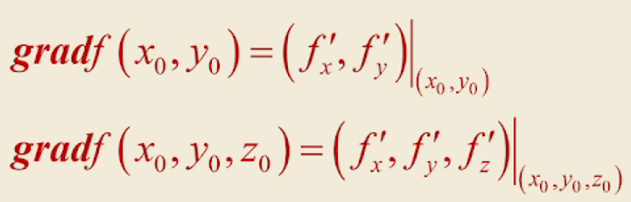
同样的表述方式
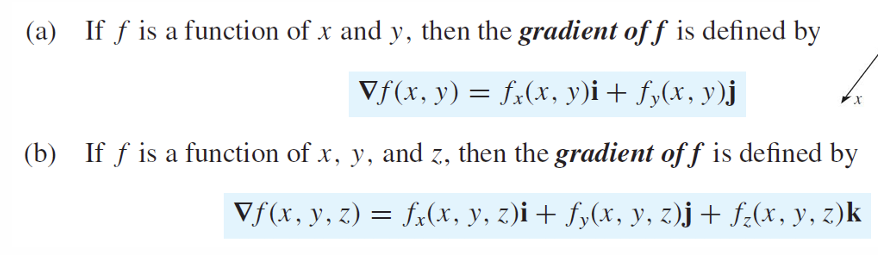
解释:
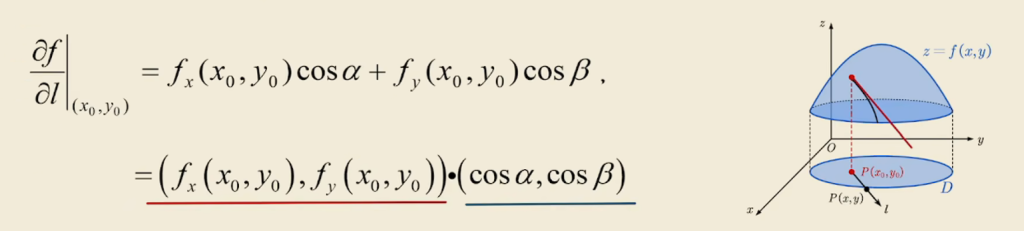
将函数某点方向导数的定理写成向量点积的形式,可以发现右侧为单位向量,左侧的向量即定义为梯度
梯度的性质:
(a) 如果在 P 点 \(\nabla f = 0\),则 f 在 P 点的所有方向导数均为零。
(b) 如果在 P 点 \(\nabla f ≠ 0\),则在 f 在 P 点的所有可能方向导数中,沿 P 点处 \(\nabla f\) 方向的导数具有最大值,该最大方向导数的值为 P 点处的 \(\|\nabla f\|\)。
(c) 如果在 P 点 \(\nabla f ≠ 0\),则在 f 在 P 点的所有可能方向导数中,沿与 P 点处 \(\nabla f\) 相反方向的导数具有最小值,该最小方向导数的值为 P 点处的 \(-\|\nabla f\|\)。

梯度是各个维度上偏导矢量的向量和,天然就是该点最大的变化率,方向也就是该点最大的变化方向。
例题:


梯度与方向导数的关系
结论:方向导数 = 梯度 点乘 单位向量
梯度:是一个向量指向变化率最大的方向即f方向导数最大的方向,大小等于f方向导数的最大值,对于一元函数而言,函数f(x)在a点处的梯度,等于该函数的导数在a点的值即\(f'(a) = \nabla f|_a\),因为方向上没得选,于是梯度直接等于导数
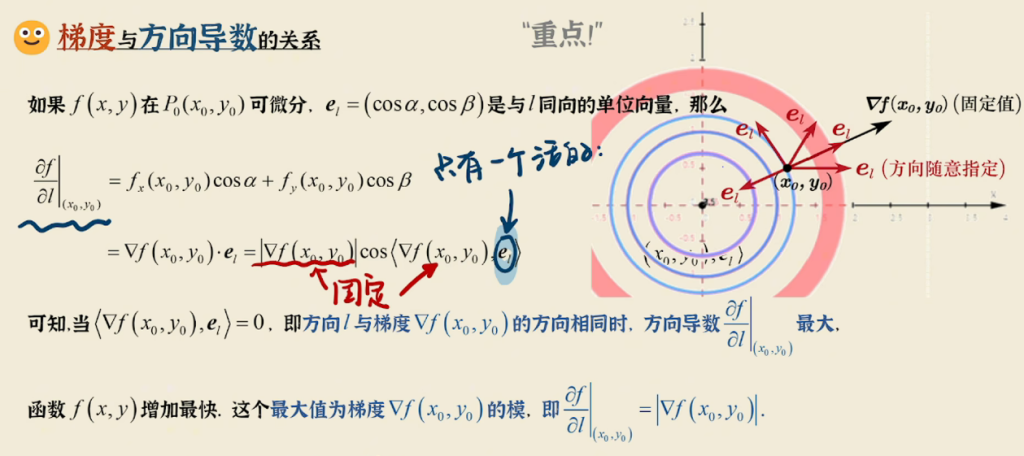
在用了5h后,最终还是通过kira老师的课明白为什么方向导数 = 梯度 点乘 单位向量了,如果将方向向量的点乘形式写成模长夹角的形式,由于单位向量的模长等于1所以省略不写,可以发现,当cos=1时方向导数最大,而此时意味着梯度与方向向量e重合,即当方向导数的方向与梯度重合时,方向导数的值最大,反过来梯度方向的方向导数也最大

总结:导数、偏导数、方向导数、梯度有何区别?
- 梯度是一个向量,其他三者都是一个数
- 偏导数和导数只能对某一坐标轴方向求导,方向导数可对自变量定义域任意方向求导,而梯度是方向导数值取最大的一个特殊情况
越靠上越强,上能推下,下不能推上。最下层互相不可推
例题:



Tangent Planes and Normal Vectors to Level Surfaces F(x, y, z) = c 等值面 \(F(x, y, z) = c\) 的切平面与法向量
平面方程表示复习:点法式(点 – 法向量形式): \(A(x – x_0) + B(y – y_0) + C(z – z_0) = 0\) 适合已知平面上一点 \((x_0, y_0, z_0)\) 和法向量 \((A, B, C)\)
\(Ax + By + Cz + D = 0\)
所以易知 \(A, B, C\) 是平面的法向量分量(即法向量 \(\boldsymbol{n} = (A, B, C)\)
什么是等值面?
给定一个三元函数 \(F(x, y, z)\),等值面是形如: \(S: F(x, y, z) = c\) 的三维空间曲面,其中 c 是常数。 它表示:所有使得函数值相同的点组成的曲面。比如:
- \(F(x, y, z) = x^2 + y^2 + z^2 \Rightarrow\) 等值面是球面。
- \(F(x, y, z) = z – x^2 – y^2 \Rightarrow\) 等值面是抛物面。
梯度 \(\nabla F\) 与切平面的关系
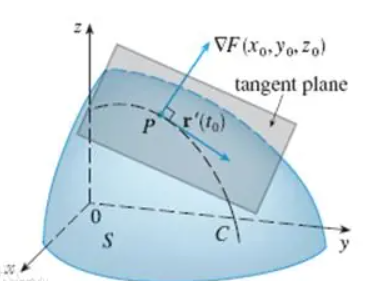
这是核心: 梯度 \(\nabla F(x_0, y_0, z_0)\) 是等值面在点 \(P_0\) 的法向量。 换句话说:
- 梯度是指向函数上升最快的方向;
- 而在等值面内(即在表面上)移动时,函数值不变 \(\Rightarrow\) 沿切平面方向导数为 0;
- 所以梯度必然垂直于切平面!
切平面方程
利用法向量 \(\boldsymbol{n} = \nabla F(x_0, y_0, z_0) = (F_x, F_y, F_z)\), 和点 \(P_0 = (x_0, y_0, z_0)\),切平面方程为: $$F_x(x_0, y_0, z_0)(x – x_0) + F_y(x_0, y_0, z_0)(y – y_0) + F_z(x_0, y_0, z_0)(z – z_0) = 0$$ 这正是用法向量 \(\times\) 点 \(=\) 平面方程的经典构造方式。
既然梯度是切平面的法向量,我们可以画出一条通过该点且沿梯度方向延伸的直线,它自然是切平面的法线。
过点 \(P_{0}\) 且平行于法向量 n 的直线垂直于切平面,我们称这条直线为法线,或更简单地称为曲面 \(F(x, y, z) = c\) 在 \(P_{0}\) 处的法线。由此可得,该直线的参数方程可表示为: $$x = x_{0} + F_{x}(x_{0}, y_{0}, z_{0})t, \quad y = y_{0} + F_{y}(x_{0}, y_{0}, z_{0})t, \quad z = z_{0} + F_{z}(x_{0}, y_{0}, z_{0})t$$