Boosting的基本思路
通过改变训练样本权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能
将多个专家的判断进行适当的综合所得出的判断要比其中任何一个专家单独的判断好
强可学习的(strongly learnable)和弱可学习的(weakly learnable)
在概率近似正确(probably approximately correct, PAC)学习的框架中,一个概念(类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,称这个概念是强可学习的;
一个概念(类),如果存在一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测略好,则称这个概念是弱可学习的。
Boosting就是从弱学习算法除法,反复学习得到一系列弱分类器(又称为基本分类器),然后组合这些弱分类器,构成一个强分类器。大多数Boosting都是改变训练数据的概率分布(训练数据的权值分布)针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
怎样获得不同的弱分类器
- 使用不同的弱学习算法得到不同基本学习器:参数估计、非参数估计…
- 使用相同的弱学习算法,但用不同的参数:K-Mean不同的K,神经网络不同的隐含层…
- 相同输入对象的不同表示凸显事物不同的特征
- 使用不同的训练集
怎样组合弱分类器
- 多专家组合Bagging:一种并行结构,所有的弱分类器都给出各自的预测结果,通过“组合器”把这些预测结果转换为最终结果。 eg.投票(voting)及其变种、混合专家模型
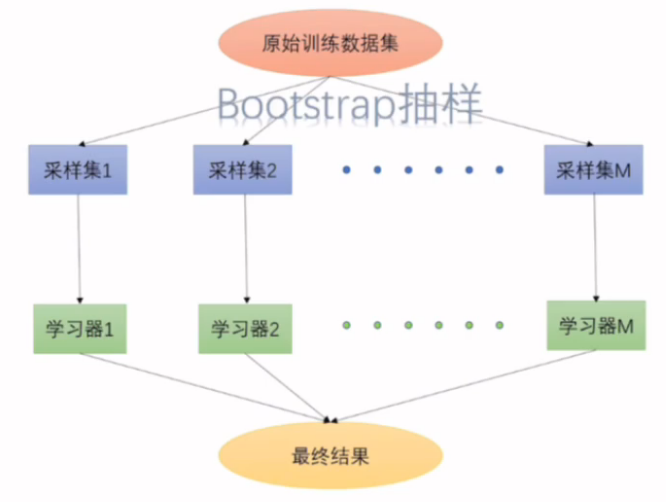
- 多级组合:一种串行结构,其中下一个分类器只在前一个分类器预测不够准(不够自信)的实例上进行训练或检测。 eg. 级联算法(cascading),Adaboast
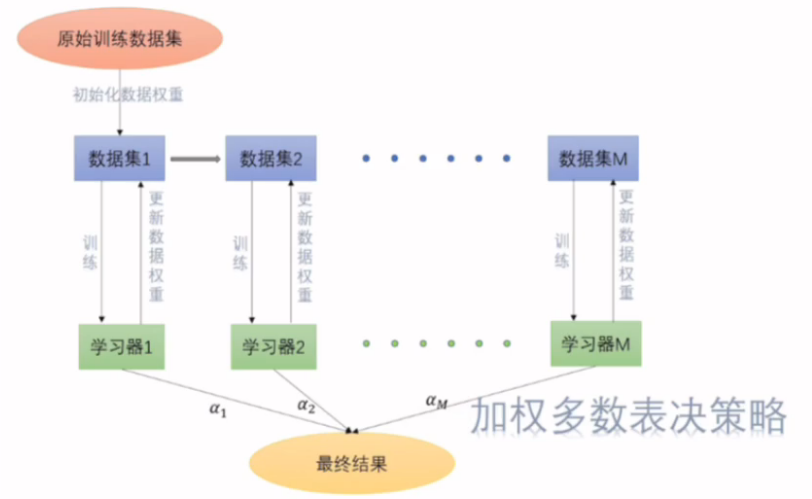
加权多数表决策略,给准确率高的学习器x更多的权重,相当于少数服从多数。
AdaBoost算法 – 代表性Boosting算法
只要找到一个比随机猜测略好的弱学习算法就可以直接将其提升为强学习算法,而不必直接去找很难获得的强学习算法。
对于boosting有两个问题需要回答:
- 每一轮如何改变训练数据的权值(概率分布)?
- 如何将弱分类器组合成一个强分类器?
对于Adaboost算法
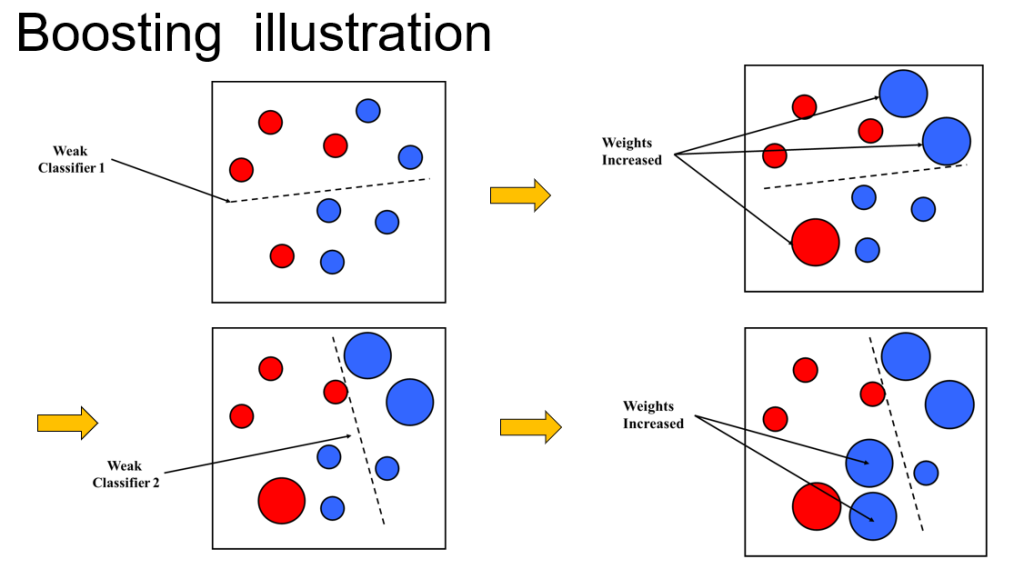
- 提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后一轮的弱分类器的更大关注。也就是说下一轮学习所用的数据集是上一轮加权后的的数据集
- 弱分类器的组合,AdaBoost 采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用;减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
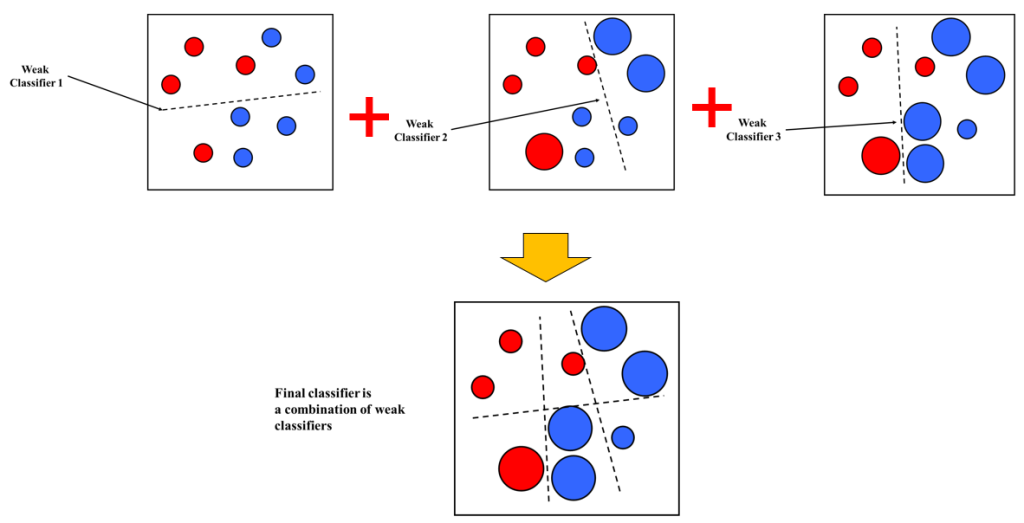
总结基本思想:AdaBoost 通过迭代地训练多个弱分类器,每一轮根据前一轮分类的结果,提高被错分样本的权重,降低被正确分类样本的权重,以便下一轮更加关注困难样本。最终, 采取加权多数表决的方法。具体地,将所有弱分类器按其性能加权线性组合成一个强分类器。分类误差小的弱分类器赋予更大的权重,误差大的赋予更小的权重。
AdaBoost 的巧妙之处就在于它将这些想法自然且有效地实现在一种算法里。
过程:



符号说明以及例子

Data集1D1中第一项数据的权重w11,和第二项数据的权重w22,以此类推
阈值v取 2.5 时分类误差率最小,预测分类与实际分类不同的项取1,相同的取0,再与对应项权重乘积的和最小。这里样本7、8、9乘以对应的w17、w18、w19得到e1=0.3。故得到基本学习器1G1(x)
根据计算G1(x)的误差率计算其在强分类器中的权重\(\alpha_1\)
由于样本数789判断错误,所以我们希望给这三个样本点加大权重,之前所有样本的权重都是相同的。通过刚刚得到的\(\alpha_1\)和数据集中的实际标签yi和预测数据集中的标签G1(xi)计算加权后的w2i构成的D2,规范化因子在最大熵模型时提到过,其作用为保证权重的和为1,在这里就是对于D这个离散概率分布的概率和为1
至此第一轮学习结束,开始第二轮学习:

D2已由上一轮循环得到,观察可得阈值v取 2.5 时分类误差率最低为3
决策函数f1(x),即最后的强分类器,是每个Gi(x)与各自对应的\(\alpha_i\)求和得到。将数据集带入计算得到误分类点个数,直到0为止方可停止学习
提升树 – 以分类树或回归树为基本分类器的提升方法
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。基本分类器x < v或x > v,可以看作是由一个根结点直接连接两个叶结点的简单决策树,即所谓的决策树桩(decision stump),决策树桩就是一棵只包含一个决策节点和两个叶子的极其简单的决策树。它只做“一次判断”,就输出结果。提升树模型可以表示为决策树的加法模型: \[ f_M(x)=\sum_{m = 1}^{M}T(x;\Theta_m) \] (8.24) 其中,\(T(x;\Theta_m)\)表示决策树,\(\Theta_m\)为决策树的参数,M为树的个数。
算法:

例题
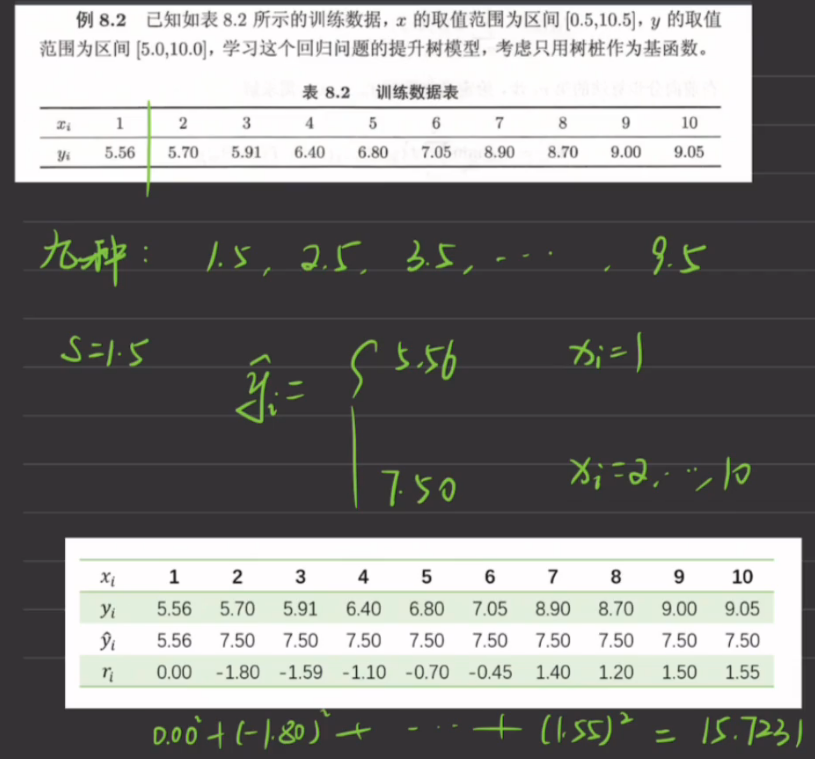
每一个分割点S都能列出这样一个表,得到该切分点下的平方损失m(注意与拟合残差r区别,拟合残差的平方和即为平方损失m),如下图。
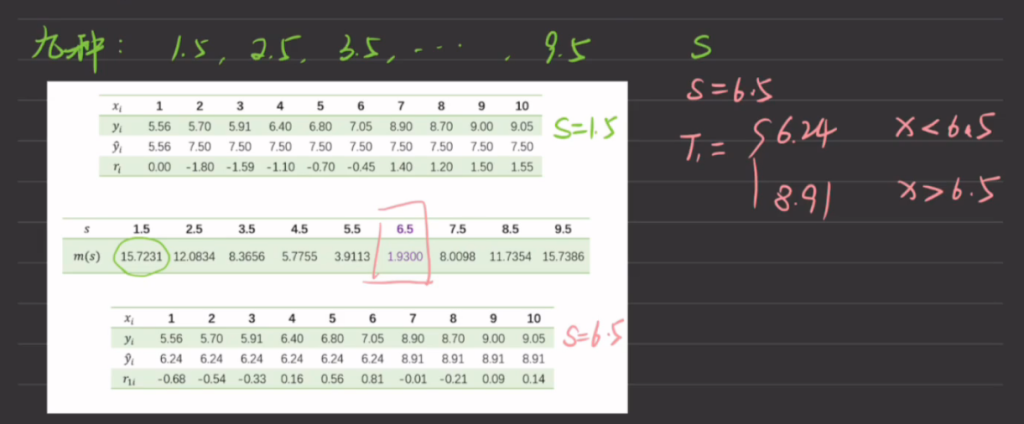
然后我们选择平方损失m最小的点作为切分点,此处选择S=6.5作为切割点,因此就可以得到第一个基回归树桩T1,输出的回归结果为两部分yi的平均值,这里X=6.5分为X1-X6和X7-X10两部分,因此当X<6.5时的回归是(y1+…+y6)/6,X≥6.5的回归是(y7+…+y10)/4(到此与回归决策树cart算法相同)
现在开始出现差别,第 2 步求\(T_2(x)\)。方法与求\(T_1(x)\)一样,只是拟合的数据是表 8.4 的残差,即T1真实值与平均值的差

第一个基回归树T1的输出是在最佳分割点切分两部分数据集,各自y的平均值。T2的输出由是第一个基回归树的拟合残差rmi(真实值与平均值的差)得到的,因此也为拟合残差的回归值。此时的学习器,由两部分的回归值的分割点共同组合而成,输出结果为T1和T2的输出之和。因此我们说新的学习器是由T1和T2合并得到的
此时真实值与回归函数值对比的拟合图形如下:
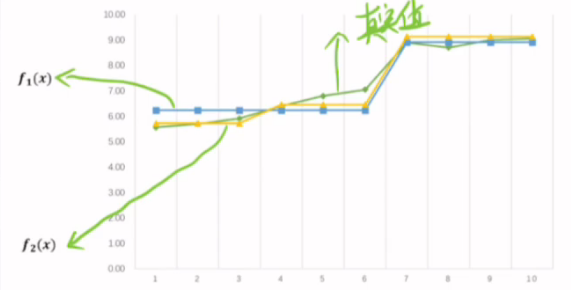
继续迭代,并记录每次添加新的最佳分割点时的平方误差m,当误差小于规定误差后即可停止,一般也不会要求0误差,因为此时会造成过拟合问题,因为每次迭代只是划分的更细了而已,倘若最终找了9个划分点,那的确可以做到0误差,但是泛化能力就会很差

Adaboost算法每个数据都没有变化,变化的只是数据的权重。而提升树数据也会跟着改变。
何为提升树,用回归树作为基础模型,正如其迭代的过程包括最终停下的条件与回归决策树相同,但是不同的是,他是将每次迭代的拟合残差作为数据源,并且不断叠加每次得到的模型









