期望最大化算法（ExpectationMaximization Algorithm）是含有隐变量的概率模型极大似然估计(核心)或极大后验概率估计的迭代算法，用于含有隐变量的模型的参数估计。含有隐变量的模型往往用于对不完全数据进行建模。EM算法是一种参数估计的思想，典型的EM算法有高斯混合模型、隐马尔可夫模型和K均值聚类等

我们用扔硬币的例子来理解EM的思想

假设有两个硬币A和B，但是他们质地不同因此正面朝上的概率不同分别为\(\theta_A\)和\(theta_B\)，为了求出他们的值，进行5次实验，每轮实验取出一枚硬币，连续抛掷5次记录结果，然后根据最大似然估计就可以计算出

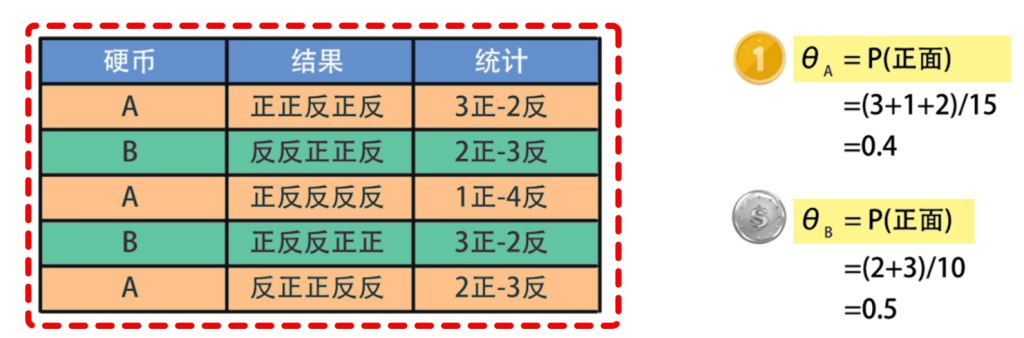
但你不知道每一轮实验中抛出的是哪一枚硬币。此时就需要引入隐变量用来代表硬币的种类

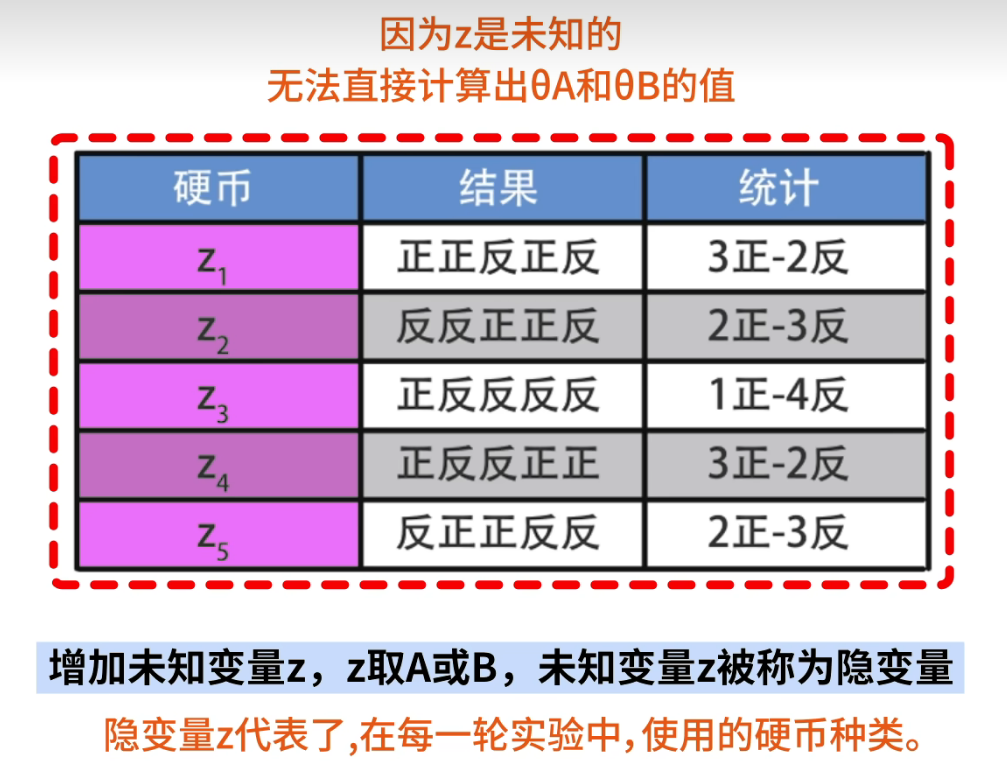
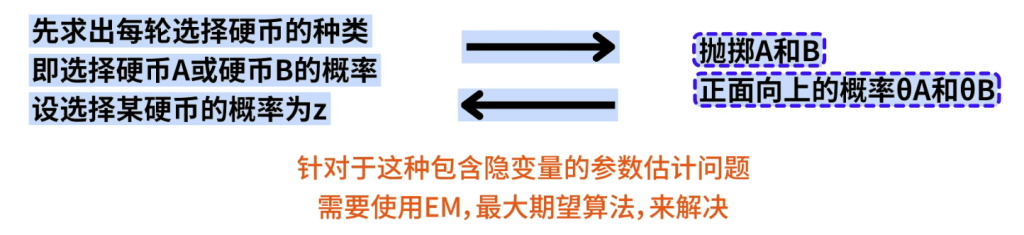
但是会造成求Z隐变量和\(\theta_A\),\(theta_B\)是相互依赖的， 这时最大似然法就无法直接应用了。

因此针对这种包含隐变量的参数估计问题我们需要使用EM最大期望算法

EM算法是一种迭代算法 包含两个步骤： 1) “E步(Expectation)” 计算 隐变量 Z的条件分布（后验概率）

计算期望 2) “M步(Maximum)” 最大化期望的对数完全似然函数

极大似然估计回顾

给定一组观测数据，我们希望找到一组参数 θ\thetaθ，使得在这些参数下，观测数据出现的概率最大。

换句话说，我们把参数当作未知量，把数据当作 “既定” 的，构造一个 “在给定参数下数据出现的可能性” 函数 —— 这就是似然函数：
\(L(\theta)=P(\text{数据}|\theta)\)
极大似然估计就是要解这个优化问题：
\(\hat{\theta}_{\text{MLE}} = \arg\max_{\theta} L(\theta)\)

本质目标就是：最大化似然函数（Likelihood Function），或者更常见地，最大化对数似然函数（Log-Likelihood Function）

除了最大似然估计，其他我们已经学过的统计估计包括最小二乘估计-最小化误差平方和(在线性回归中使用)，贝叶斯估计

算法：

EM 算法通过迭代求解观测数据的对数似然函数\(L(\theta)=\log P(Y|\theta)\)的极大化，实现极大似然估计。每次迭代包括两步：E 步，求期望，即求\(\log P(Y,Z|\theta)\)关于\(P(Z|Y,\theta^{(i)})\)的期望： \(Q(\theta,\theta^{(i)})=\sum_{Z}\log P(Y,Z|\theta)P(Z|Y,\theta^{(i)})\) 称为Q函数，这里\(\theta^{(i)}\)是参数的现估计值；M 步，求极大，即极大化Q函数得到参数的新估计值： \(\theta^{(i + 1)}=\underset{\theta}{\arg\max}Q(\theta,\theta^{(i)})\)

在构建具体的 EM 算法时，重要的是定义Q函数。每次迭代中，EM 算法通过极大化Q函数来增大对数似然函数\(L(\theta)\)。

EM 算法在每次迭代后均提高观测数据的似然函数值，即 \(P(Y|\theta^{(i + 1)})\geq P(Y|\theta^{(i)})\)

符号说明(抛硬币为例)：

• Y（X） :硬币每次观测出的结果，表示为正反面序列
• Z 是隐变量数据，代表 A 硬币或 B 硬币
•  \(\theta_A,\theta_B\) 是对应 A 硬币和 B 硬币正面朝上的概率

思路解释：

输入：观测变量数据 Y，隐变量数据 Z，联合分布 \(P(Y,Z|\theta)\)，条件分布 \(P(Z|Y,\theta)\)

E步做的事：

• 用当前的旧参数\(\theta^{(i)}\)；
• 计算隐变量Z在观测Y条件下的后验分布\(\mu_j^{(i + 1)} = P(Z_j = B\mid y_j, \theta^{(i)})\)。在后面的例题中用贝叶斯计算\(\mu_j^{(i + 1)} = \frac{\pi^{(i)}\cdot p^{(i)^{y_j}}(1 – p^{(i)})^{1 – y_j}}{\pi^{(i)}\cdot p^{(i)^{y_j}}(1 – p^{(i)})^{1 – y_j}+(1 – \pi^{(i)})\cdot q^{(i)^{y_j}}(1 – q^{(i)})^{1 – y_j}}\)
  • \(P(Z|Y,\theta)\) —— 条件概率（后验概率）
  • 也就是说：
  • 我们观测到了 Y，但看不到 Z，只能根据当前的参数 θ(i)估计每个可能的隐变量取值的概率。 即：在知道实验抛出了正面 / 反面后，它到底是从硬币 B 抛出来的，还是硬币 C 抛出来的概率。
• 然后用这个分布对\(\log P(Y,Z|\theta)\)求期望；
  • \(P(Y,Z|\theta)\) —— 完整数据的联合概率
  • 也就是：在参数\(\theta\)下，生成某个观测值Y且隐变量是Z的概率。
  • 在三硬币模型中，这个意思就是：同时知道实验结果是 “正面” 或 “反面”Y，并且知道选的是 B 或 C 硬币（即Z），在当前参数\(\theta\)下的概率。这个是我们想最大化的目标函数中对数部分的内容（M 步）。
• 这就构造出目标函数\(Q(\theta,\theta^{(i)})\)。

M步做的事：

最大化这个目标函数\(Q(\theta,\theta^{(i)})\)，也就是： \(\theta^{(i + 1)}=\arg\max_{\theta}Q(\theta,\theta^{(i)})\) 目的：找到一组新的参数\(\theta^{(i + 1)}\)，能让在当前对Z的 “理解” 下，完整数据的似然最大。后面的做法是对参数θ求偏导数，\(\theta = (\pi, p, q)\)

那你就在 M 步中分别对这三个变量求偏导： \(\begin{cases} \frac{\partial Q}{\partial \pi}=0 \\ \frac{\partial Q}{\partial p}=0 \\ \frac{\partial Q}{\partial q}=0 \end{cases}\) 解这三个方程，就得到：

\(\pi^{(i + 1)}\) \(p^{(i + 1)}\) \(q^{(i + 1)}\)

输出：模型参数 \(\theta\)

推导

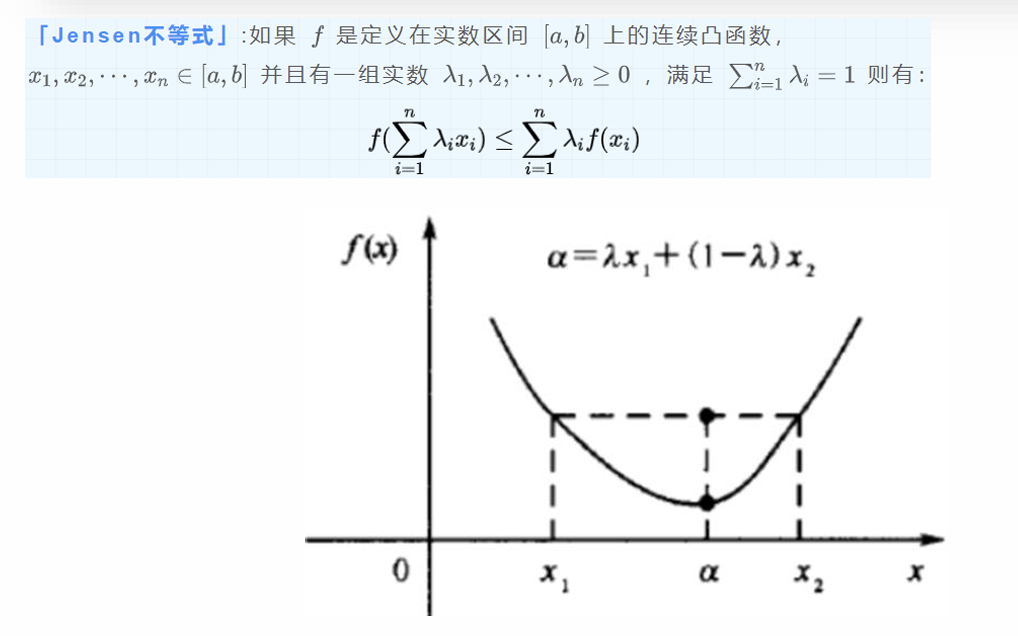
E步

大致的思路讲解，并不严格按照正式步骤：

最初随机设置一组PA和PB的值，基于这组概率我们就能通过最大似然估计求出每轮对于硬币种类的选择

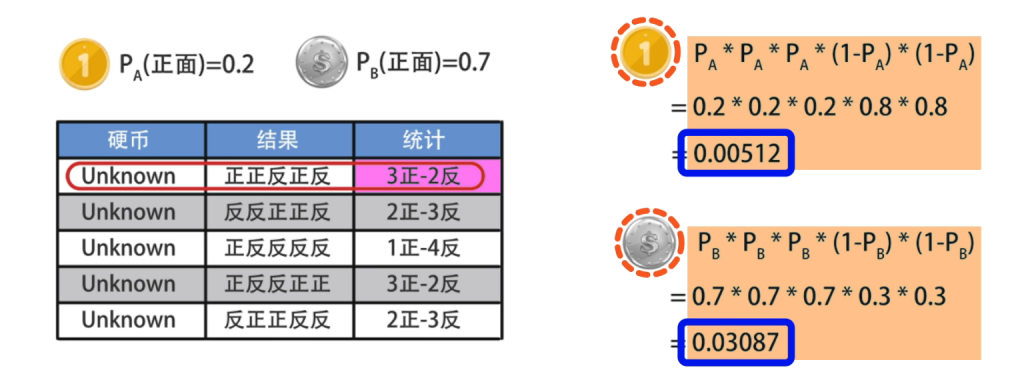
假设第一组Z为B的概率明显大于Z为A的概率，也就是说在PA=0.2，PB=0.7的初始条件下，为了出现3正两反的结果，抛掷时更有可能使用的是硬币B，同理可以计算出2、3、4、5轮结果下最有可能使用的硬币种类

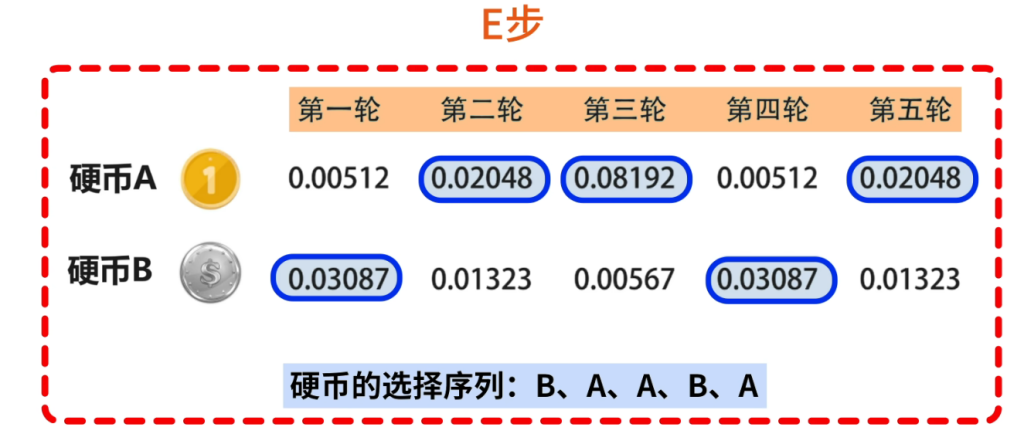
M步

再根据得到的隐变量的选择序列后依然使用最大似然估计重新计算PA和PB的结果

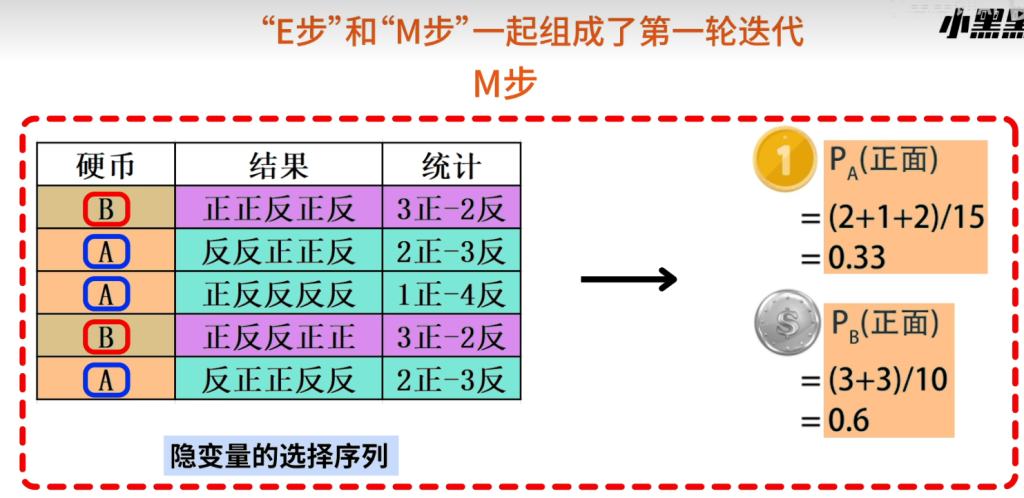
如此循环迭代最终可以计算出接近真实值的PA和PB

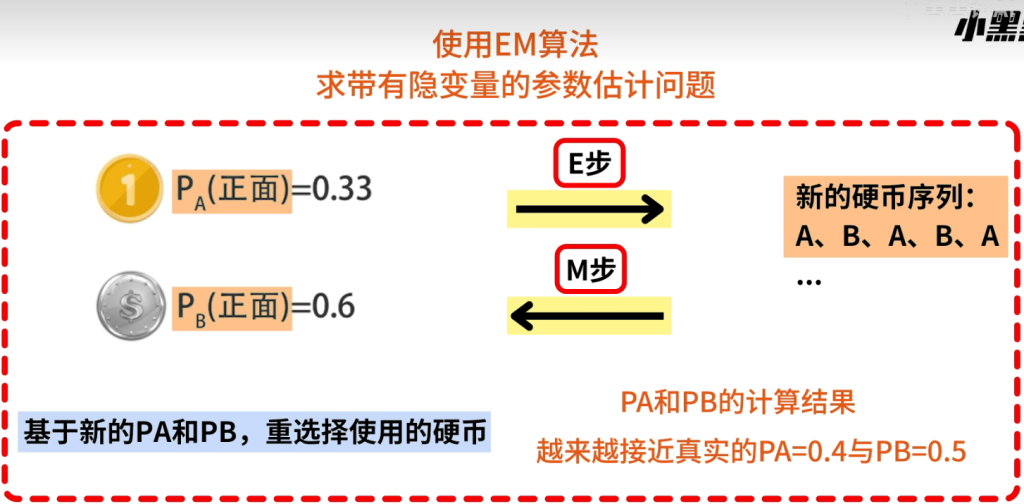
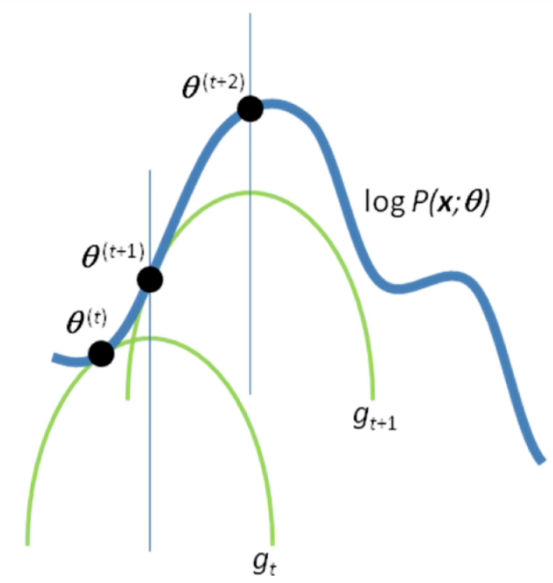
新估计出的PA和PB： 一定会更接近真实的PA和PB 按照EM算法迭代下去： 不一定刚好收敛到最初设想的真实值最终的结果，取决于初始化的情况

EM算法案例-两硬币模型

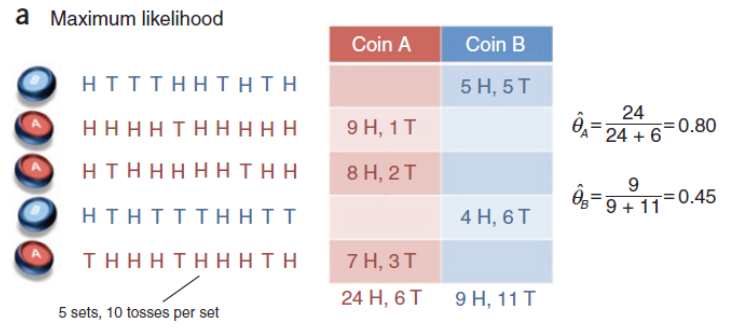
假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的掷硬币实验：共做 5 次实验，每次实验独立的掷十次，结果如图中 a 所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H (H代表正面朝上)。a 是在知道每次选择的是A还是B的情况下进行，b是在不知道选择的是A还是B的情况下进行，问如何估计两个硬币正面出现的概率？

知道每次实验的硬币种类：

不知道每次实验的硬币种类：

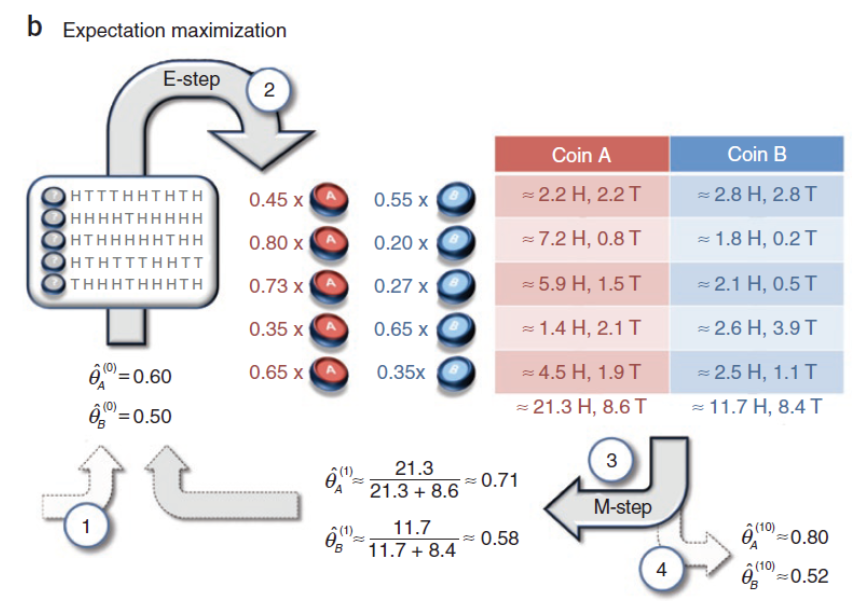
只不过写出了其中一个（$\rho_j$）后，另一个就可以由 $1 – \rho_j$ 得到。

注意在知道每次实验的硬币种类的情况中，参数为\(\hat{\theta}_A = \frac{A\text{的正面数}}{A\text{的总次数}}\)，\(\hat{\theta}_B = \frac{B\text{的正面数}}{B\text{的总次数}}\)。

三硬币模型

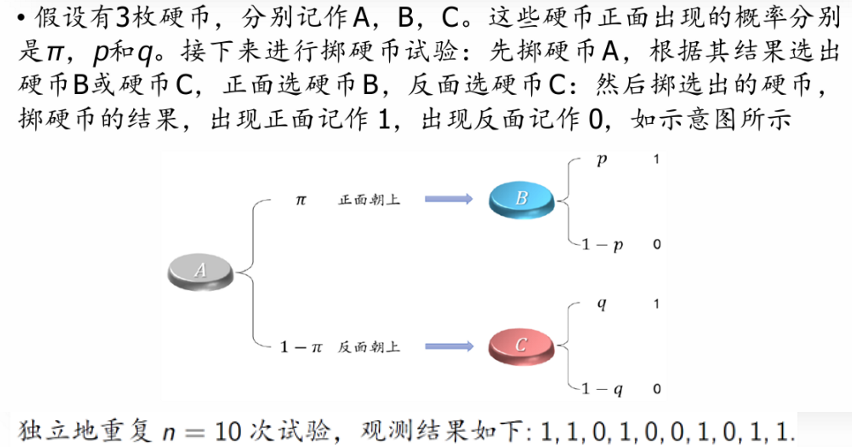
在 M 步更新参数时，比如更新 $\pi$，我怎么知道代入的是 $z = \text{B}$ 的概率（$\rho_j$），而不是 $z = \text{C}$ 的？因为$\pi$ 的定义是“从 A 抛出后选到硬币 B 的概率”，所以更新它就要用有多少次是“来自硬币 B”的期望次数来平均。

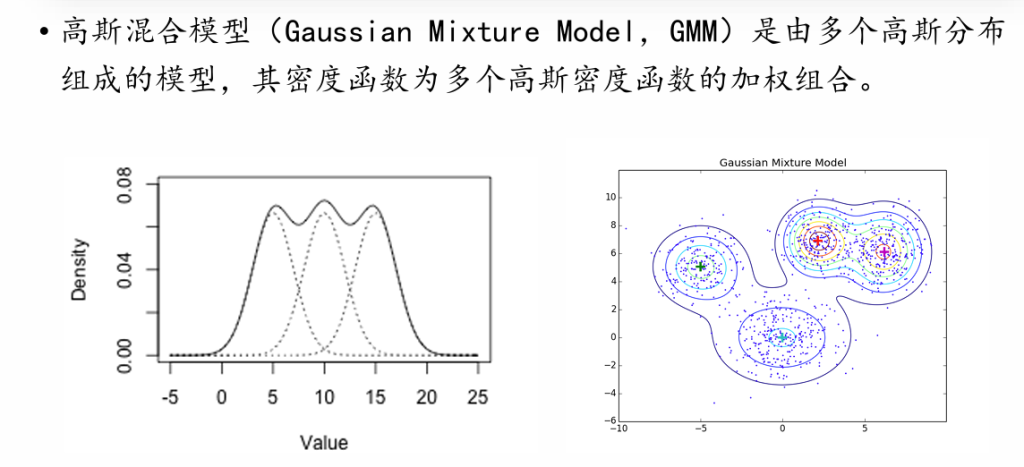
EM算法应用：高斯混合模型

符号	含义
y	一个观测数据点
K	高斯分布的数量（即有 K 个“簇”或“成分”）
\(\alpha_k\)	第 k 个高斯分布的“权重”或“概率”，满足：\(\alpha_k \geq 0\), 且 \(\sum_{k=1}^{K} \alpha_k = 1\)
\(\theta_k = (\mu_k, \sigma_k^2)\)	第 k 个高斯分布的参数：均值和方差
\(\phi(y \mid \theta_k)\)	第 k 个高斯分布在 y 处的密度值，也就是第 k个高斯分布的“概率密度函数”

这是我们熟悉的一维高斯分布密度公式。

例题：