前几章的数据元素都是原子类型,元素的值是不再分解的
数组和广义表是一种特殊的线性表,即线性表中数据元素本身也是一个数据结构
一个n维数组类型可以定义为其数据元素为n-1维数组类型的一维数组类型
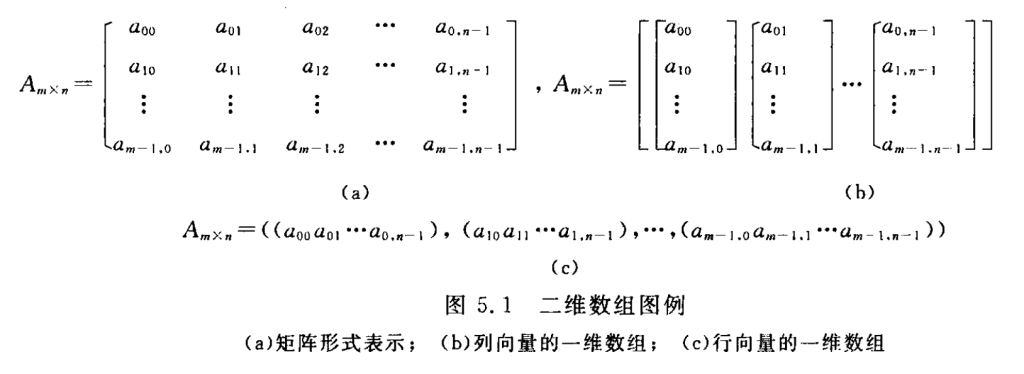
和线性表一样,所有的数据元素必须属于同一类型
数组一旦被定义,她的维度和长度就不再改变
数组只有存取元素和修改元素的操作
数组的顺序表示和实现
由于数组不作插入和删除操作,因此一旦建立了数组,结构中的数据元素个数与元素之间的关系就不再发生变动,因此普遍采用顺序存储结构
由于存储单元是一维的结构,而数组是个多维的结构,则用一组连续存储单元存放数组的数据元素就有个次序约定问题。对二维数组可有两种存储方式:
- 一种以列序为主序(column major order)的存储方式
- 一种是以行序为主序(row major order)的存储方式
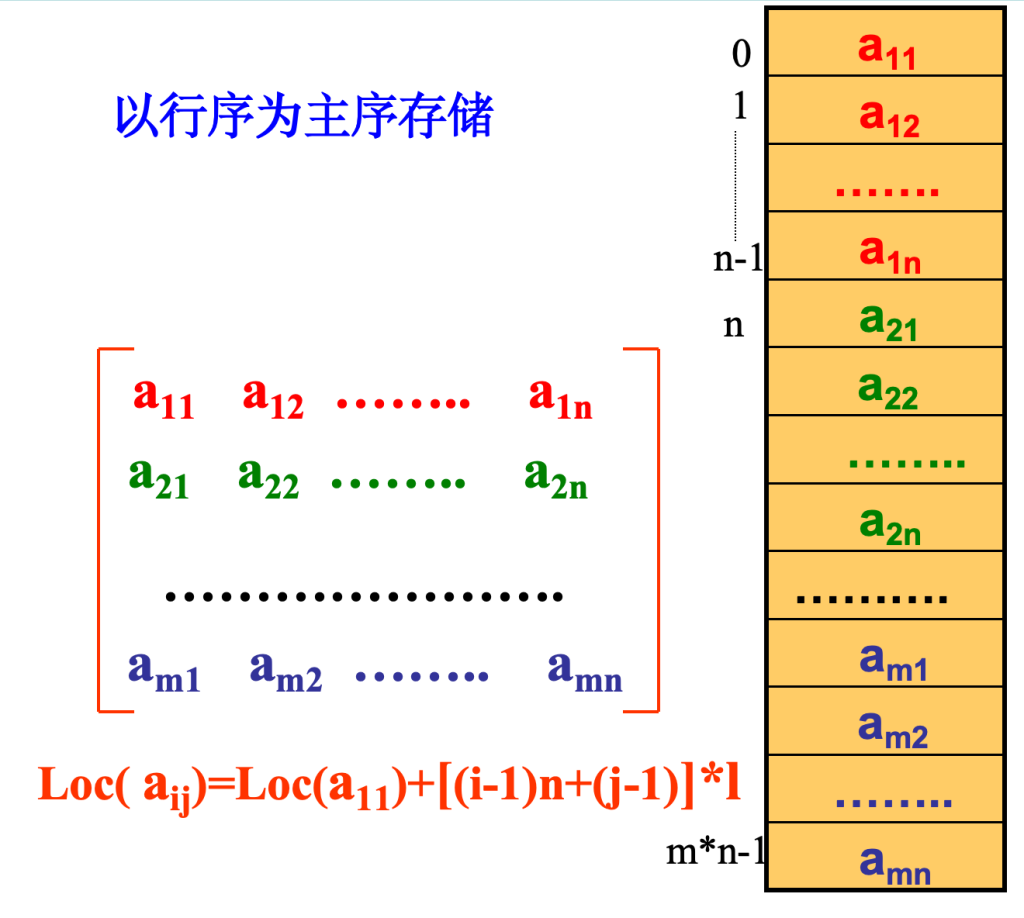
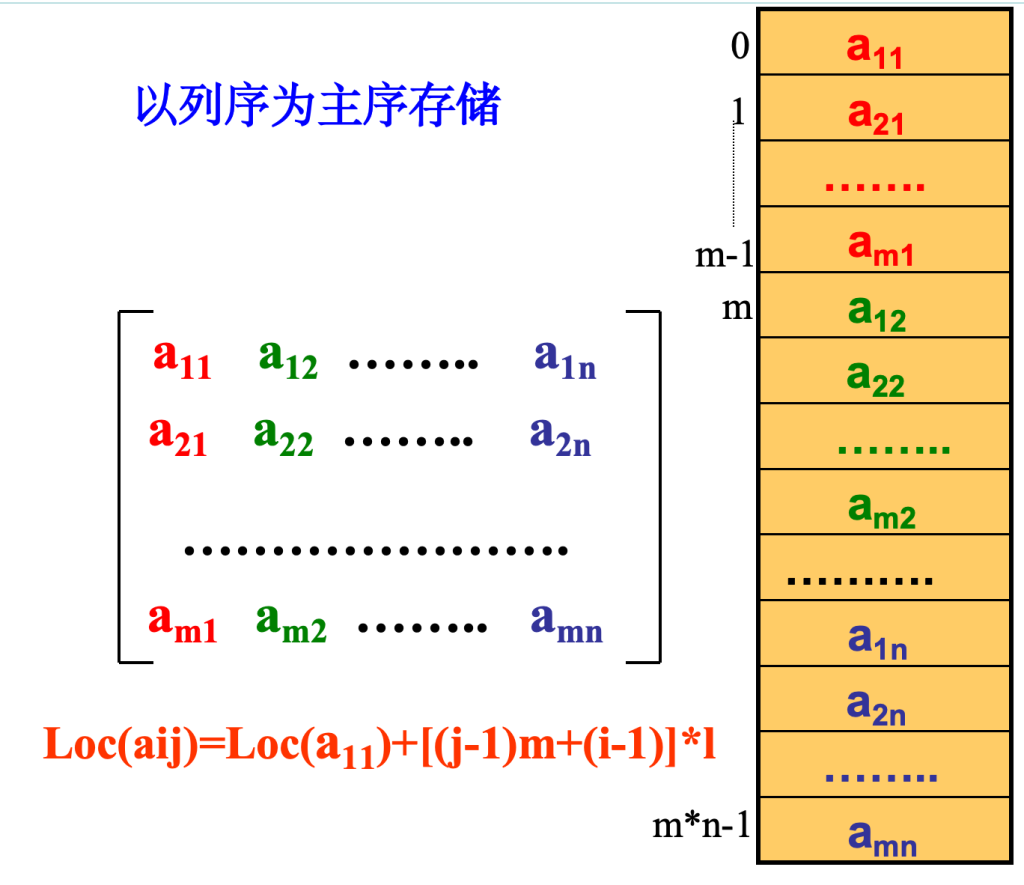
-1是因为实际行列数 = index + 1 (图中a11的下标实际应为a00)
总偏移量(aᵢⱼ之前的所有元素占用的存储单元数):总元素数 = 第 j 列之前的元素数 + 第 j 列中 aᵢⱼ之前的元素数
矩阵的压缩存储
有时为了节省存储空间,可以对这类矩阵进行压缩存储。所谓压缩存储是指:为多个值相同的元只分配一个存储空间;对零元不分配空间。
假若值相同的元素或者零元素在矩阵中的分布有一定规律,则我们称此类矩阵为特殊矩阵;反之,称为稀疏矩阵。下面分别讨论它们的压缩存储。
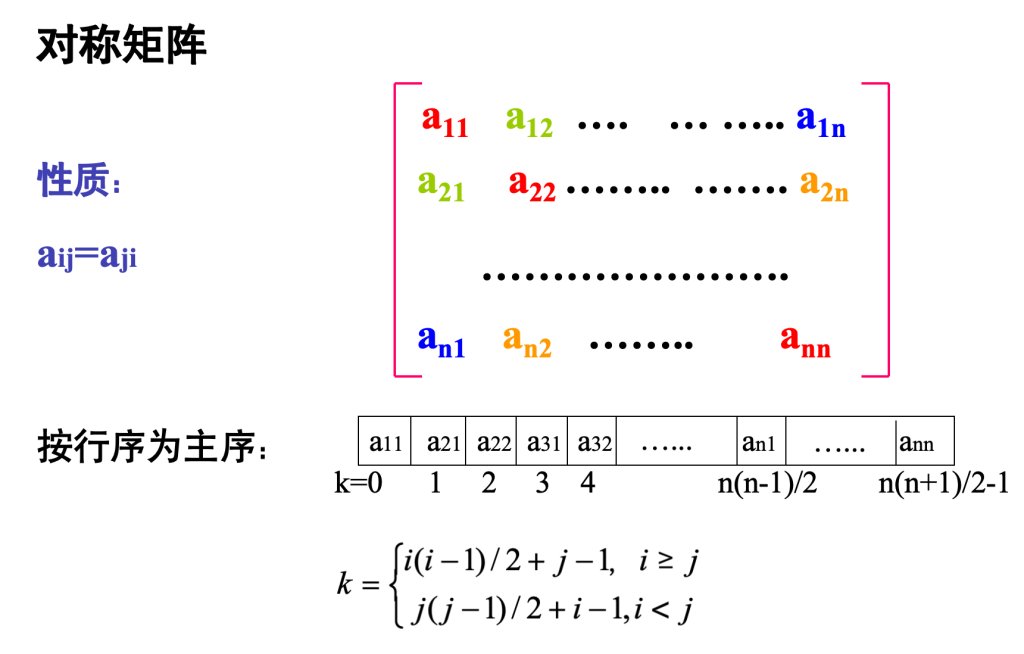
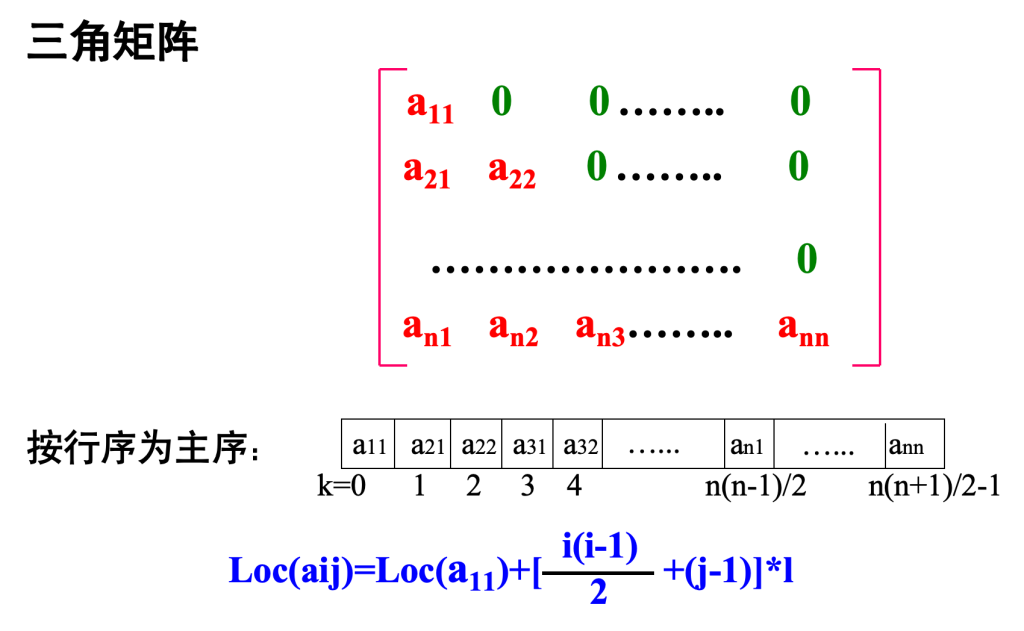
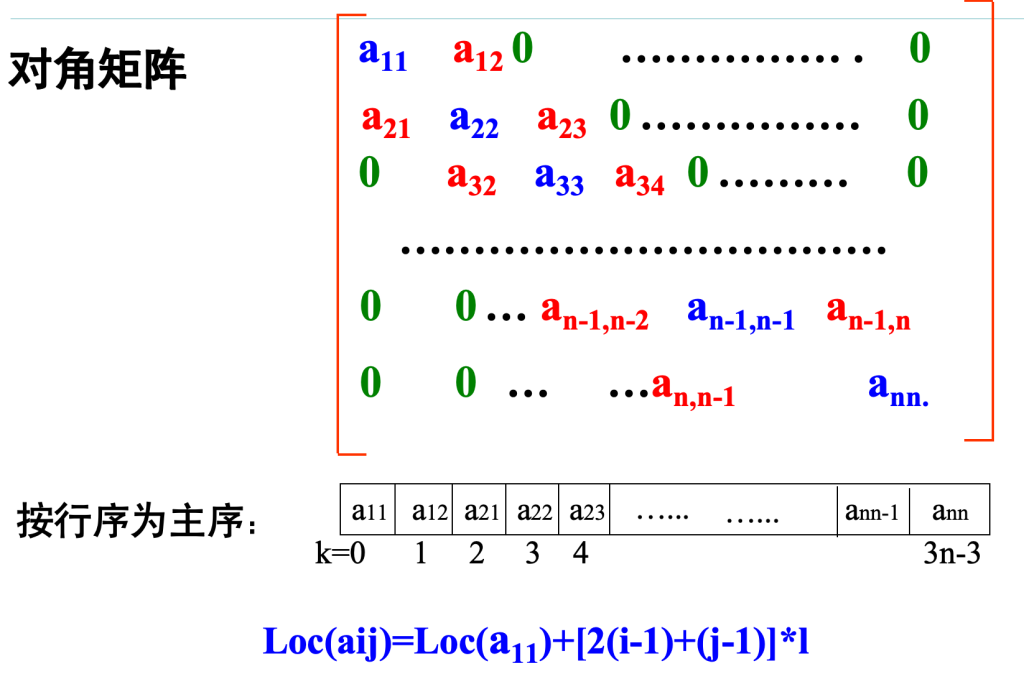
特殊矩阵
稀疏矩阵
非0元较0元少,且分布没有一定规律的矩阵
压缩存储原则:只存矩阵的行列维数和每个非零元的行列下标及其值
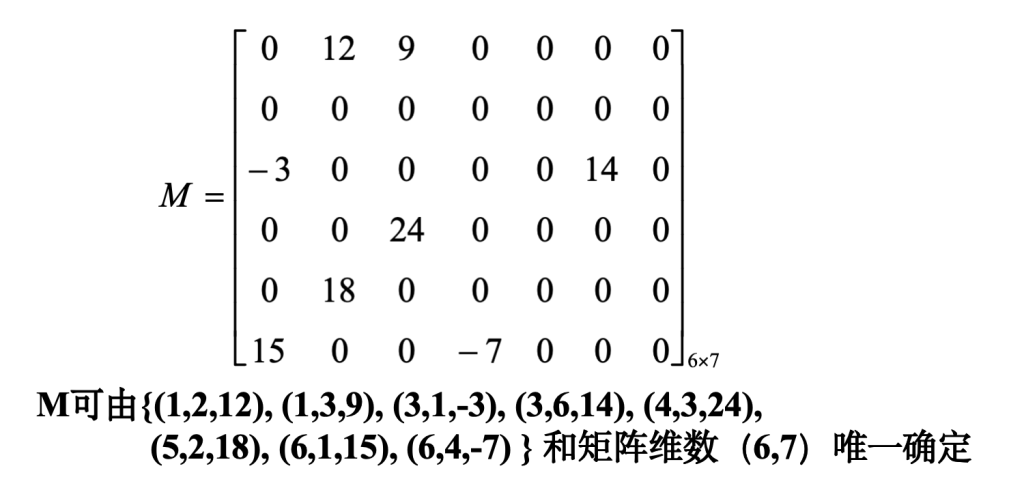
而由上述三元组表的不同表示方法可引出稀疏矩阵不同的压缩存储方法。
顺序存储结构表示三元表
在此,data域中表示非零元的三元组是以行序为主序顺序排列的,从下面的讨论中读者容易看出这样做将有利于进行某些矩阵运算。下面将讨论在这种压缩存储结构下如何实现矩阵的转置运算。
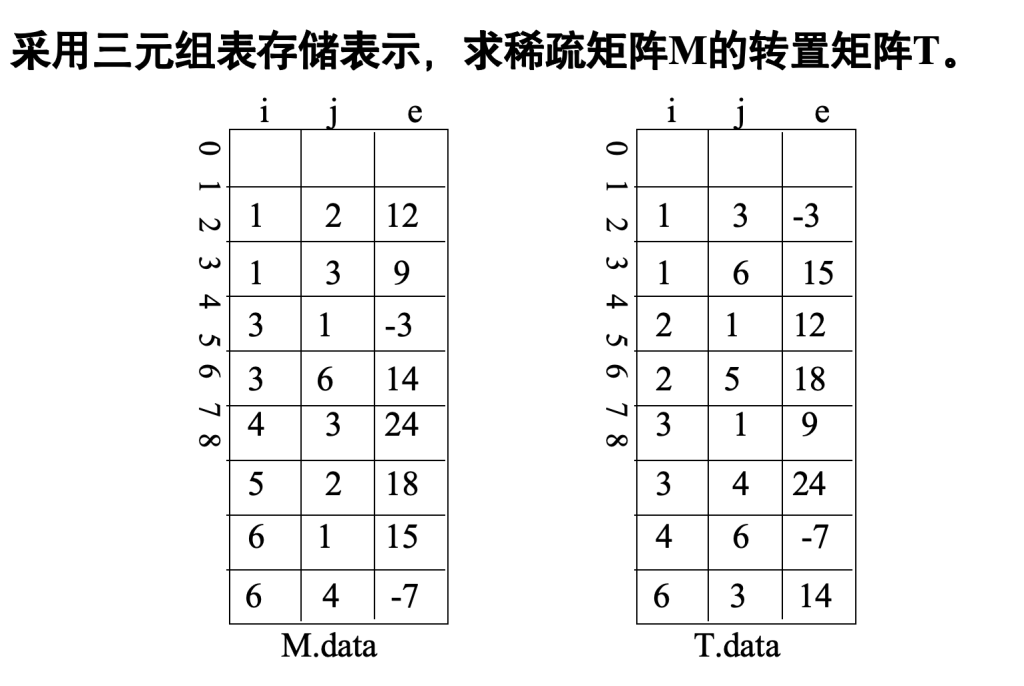
问题描述:已知一个稀疏矩阵的三元组表,求该矩阵转置矩阵的三元组表
一般矩阵转置算法

一个 mu行、nu列 的普通矩阵(每个位置都存元素,不管是不是 0),转置就是把 “第 row 行第 col 列” 的元素,放到 “第 col 行第 row 列”。
它的循环是:先遍历每一列(col),再遍历每一行(row),逐个交换位置。
因为要把所有 mu×nu 个元素都转一遍,所以时间复杂度是 O (mu×nu)
稀疏矩阵的转置算法:
稀疏矩阵的特点是 “大部分元素是 0,只存非 0 元素(共 tu 个)”,用三元组(行、列、值)存这些非 0 元素。想按 “原矩阵的列” 取元素,但原列表是按 “原矩阵的行” 存的
它的转置算法是:先遍历原矩阵的每一列(col),再把所有非 0 元素都扫一遍(找 “列 = col” 的元素),然后交换行列存到新三元组里。
所以时间复杂度是 O(nu×tu)(外层循环 nu 次列,内层循环 tu 次非 0 元素)
比如要找原矩阵第 1 列的元素,就把 a.data 里所有 “j=1” 的三元组(比如 a.data 里的 (3,1,-3)、(6,1,15))挑出来,交换 i 和 j,放到 b.data 里;
再找原矩阵第 2 列的元素,挑 a.data 里 “j=2” 的三元组(比如 (1,2,12)、(5,2,18)),交换 i 和 j 放到 b.data 里…
// 函数功能:将稀疏矩阵M转置,结果存到矩阵T中;Status是函数返回状态(成功/失败)
Status TransposeSMatrix(TSMatrix M, TSMatrix &T)
{
// 1. 初始化转置矩阵T的基本信息:
// T的行数 = 原矩阵M的列数;T的列数 = 原矩阵M的行数;T的非零元素个数 = M的非零元素个数
T.mu = M.nu;
T.nu = M.mu;
T.tu = M.tu;
// 2. 如果存在非零元素(需要转置)
if (T.tu) {
q = 1; // q是转置矩阵T的data数组的下标(记录当前要存到T的第几个位置)
// 3. 按“原矩阵M的列”遍历(col是原矩阵M的列号)
for (col = 1; col <= M.nu; col++) {
// 4. 遍历原矩阵M的所有非零元素(p是M的data数组的下标)
for (p = 1; p <= M.tu; p++) {
// 5. 找到原矩阵M中“列号等于当前col”的元素
if (M.data[p].j == col) {
// 6. 把该元素的行列交换,存到T的data数组中:
T.data[q].i = M.data[p].j; // 转置后元素的行 = 原元素的列
T.data[q].j = M.data[p].i; // 转置后元素的列 = 原元素的行
T.data[q].e = M.data[p].e; // 元素值不变
q++; // T的下标后移,准备存下一个元素
}
}
}
}
// (注:函数末尾一般会返回成功状态,比如return OK; 这里代码可能省略了)
}重点:什么时候这个算法不好用?
如果矩阵 “不稀疏” 了 —— 比如非 0 元素的个数 tu 和 mu×nu 差不多(比如矩阵里没几个 0),那 tu ≈ mu×nu。
这时候,三元组转置的时间复杂度就变成:
O(nu×tu) ≈ O(nu×mu×nu) = O(mu×nu²)。
而普通矩阵转置的时间复杂度是 O(mu×nu),显然 O(mu×nu²) 比 O(mu×nu) 慢很多(多了一个 “nu” 的倍数)。
所以这个 “三元组转置算法”,只适合 “非 0 元素特别少” 的情况(tu 远小于 mu×nu),这时候它比普通矩阵转置快;如果非 0 元素多了,它反而更慢。
快速转置算法
之前的普通转置是 “挨个找每一列的快递”,很慢;快速转置是 “先算好每一列快递的存放位置”,直接放,效率更高。
快速转置分两步:
- 统计每一列的非零元素数量(知道每列有多少个 “快递”);
- 算好每一列第一个非零元素在 T 里的位置(知道每列的 “快递堆” 从哪开始放);然后按原顺序遍历非零元素,直接放到对应的位置。
为此需要设两个数组
num[col]:表示矩阵M中第col列中非零元个数
cpot[col]:指示M中第col列第一个非零元在T.data中位置
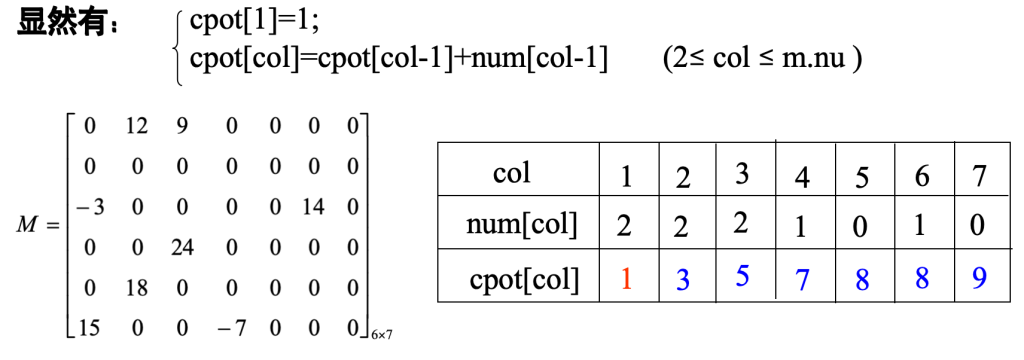
- 第 1 列的第一个元素,从 T 的第 1 个位置开始放(cpot [1]=1);
- 第 2 列的起始位置 = 第 1 列的起始位置 + 第 1 列的元素数量(cpot [2]=1+2=3);
- 第 3 列的起始位置 = 第 2 列的起始位置 + 第 2 列的元素数量(cpot [3]=3+2=5);以此类推,就能算好每一列元素在 T 里的 “起始堆放点”。
// 函数功能:快速转置稀疏矩阵M,结果存到矩阵T中;Status是返回状态(成功/失败)
Status FastTranposeSMatrix(TSMatrix M, TSMatrix &T)
{
// 1. 初始化转置矩阵T的基本信息:
// T的行数 = 原矩阵M的列数;T的列数 = 原矩阵M的行数;T的非零元素数 = M的非零元素数
T.mu = M.nu;
T.nu = M.mu;
T.tu = M.tu;
// 2. 如果存在非零元素(需要转置)
if (T.tu) {
// 2.1 初始化num数组:统计每列非零元素的数组,先全部置0
for (col = 1; col <= M.nu; ++col)
num[col] = 0;
// 2.2 遍历M的所有非零元素,统计每列的非零元素数量(num[col]是第col列的非零元素数)
for (t = 1; t <= M.tu; ++t)
++num[M.data[t].j]; // M.data[t].j是第t个元素的列号,对应列的计数+1
// 2.3 初始化cpot数组:第1列的第一个非零元素,在T中的起始位置是1
cpot[1] = 1;
// 2.4 计算每列第一个非零元素在T中的起始位置
for (col = 2; col <= M.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1]; // 第col列的起始位置 = 前一列起始位置 + 前一列元素数
// 2.5 按M的非零元素顺序,逐个放到T的对应位置
for (p = 1; p <= M.tu; ++p) {
col = M.data[p].j; // 当前元素属于原矩阵的第col列
q = cpot[col]; // 取该列在T中的当前存放位置
// 转置:行列交换,值不变,存到T的第q个位置
T.data[q].i = M.data[p].j; // 转置后的行 = 原元素的列
T.data[q].j = M.data[p].i; // 转置后的列 = 原元素的行
T.data[q].e = M.data[p].e; // 元素值不变
++cpot[col]; // 该列的存放位置后移一位,准备放下一个同列元素
}//for
}//if
return OK; // 返回成功状态
}//FastTranposeSMatrix这个算法仅比前一个算法多用了两个辅助向量①。从时间上看,算法中有4个并列的单循环,循环次数分别为nu和tu,因而总的时间复杂度为O(nu+tu)。在M的非零元个数tu和mu×nu等数量级时,其时间复杂度为O(mu×nu),和经典算法的时间复杂度相同。









