前言：栈和队列是限定插入和删除只能在表的“端点”进行的线性表（是线性表的子集，是插入和删除位置受限的线性表）

栈

定义：限定仅在栈顶进行插入或删除操作的线性表（所以栈与一般线性表区别仅在于运算规则不同）
表尾称为栈顶top，表头又称为栈底
固定的一端称为栈底，变化的一端称为栈顶
栈存入的新元素永远放在栈顶，栈底是栈的起始位置，一旦确定后不会因入栈操作改变

逻辑结构：同线性表相同，仍为一对一关系
存储结构：用顺序栈或链栈存储均可，但以顺序栈更常见

特点后进先出LIFO

ADT Stack{
    数据对象: D={ai | ai ∈ ElemSet, i = 1,2 … n n>=0}
    数据关系: R1 = {< ai-1, ai > | ai-1, ai ∈ D}
              约定an端为栈顶, a1端为栈底
    基本操作:
        InitStack(&S); DestroyStack (&S);
        Push (&S, e); Pop (&S, &e);
        ……等等
}ADT Stack

- InitStack(&S):
  ✓ 操作结果: 构造一个空栈S
- DestroyStack (&S)
  ✓ 初始条件: 栈S已经存在
  ✓ 操作结果: 销毁栈S
- ClearStack (&S)
  ✓ 初始条件: 栈S已经存在
  ✓ 操作结果: 将栈S清为空栈

StackEmpty(S):
✓ 初始条件: 栈S已经存在
✓ 操作结果: 若栈S为空栈, 返回TRUE; 否则返回FALSE
StackLength (S)
✓ 初始条件: 栈S已经存在
✓ 操作结果: 返回栈S中的元素个数, 即栈的长度
GetTop (S, &e)
✓ 初始条件: 栈S已经存在且非空
✓ 操作结果: 用e返回栈S的栈顶元素

Push(&S, e):
✓ 初始条件: 栈S已经存在
✓ 操作结果: 插入元素e为新的栈顶元素
Pop (&S, &e)
✓ 初始条件: 栈S已经存在且非空
✓ 操作结果: 删除S的栈顶元素, 并用e返回其值
StackTraverse(S, visit())
✓ 初始条件: 栈S已经存在且非空
✓ 操作结果: 从栈底到栈顶依次对S的每个数据元素调用函数visit(),
  旦visit()失败, 则操作失败。

栈的表示和实现：

typedef struct {
    SElemType *base; //栈底的指针
    SElemType *top;  //栈顶的指针
    int stacksize;
} SqStack;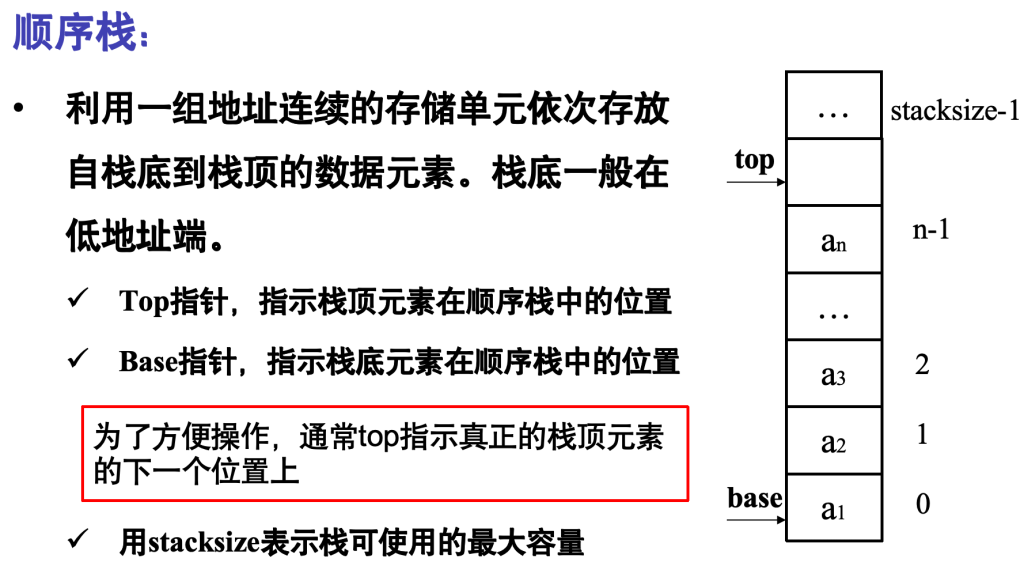

Top = base表示空栈 
栈满：top-base=stacksize

相应基本操作的实现算法

初始化时栈顶指针被设置为栈底指针位置，随着新增元素，栈顶指针自增
但这点在共享栈中可能会改变，新增元素放在栈顶，栈顶指针自减

Status InitStack (SqStack &S){
    //构造一个空栈
    S.base=(SElemType *)malloc(
            STACK_INIT_SIZE*sizeof (SElemType));
    if (!S.base) exit (OVERFLOW);
    S.top = S.base ;
    S.stacksize = STACK_INIT_SIZE ;
    return OK;
}

Status GetTop (SqStack S, SElemType &e){
    //若栈不空，用e返回S的栈顶元素
    if (S.top == S.base) return ERROR;
    e = *(S.top - 1);
    return OK;
}

Status Push (SqStack &S, SElemType e){
    //插入元素e为新的栈顶元素
    if (S.top - S.base >= S.stacksize) { //栈满，追加存储空间
        S.base = (SElemType *) realloc (S.base,
            (S.stacksize+STACKINCREMENT)*sizeof(SElemType));
        if (!S.base) exit (OVERFLOW);
        S.top = S.base + S.stacksize ;
        S.stacksize += STACKINCREMENT;
    }
    *S.top ++ = e ; //每当插入新的栈顶元素时，指针top增1
    return OK;
}

Status Pop (SqStack &S, SElemType &e){
    //若栈不空，则删除S的栈顶元素，用e返回其值
    if (S.top == S.base) return ERROR;
    e = * -- S.top ;//每当删除栈顶元素时，指针top减1
    return OK;
}

链栈中指针不再指向下一个位置，因为方便
指针的方向和单链表相反，因为操作都在栈顶，否则每次操作都需要O(n)时间定位到栈顶

栈的应用实例

表达式求值：只对四则运算表达式求值

假定输入的表达式没有语法错误，实现算符优先算法，使用两个工作栈
OPTR：寄存运算符
OPND：寄存操作数或运算结果
算法基本思想：
首先置操作数栈为空栈，表达式起始符为运算符栈的栈底元素
依次读入表达式中每个字符，若是操作数则进OPND栈，若是运算符则和OPTR栈的栈顶运算符比较优先权后作相应操作，直到整个表达式求值完毕（即OPTR栈的栈顶元素和当前读入的字符均为“#”）

// 计算表达式的值并返回结果，返回值类型为OperandType
OperandType EvaluateExpression()
{
    // 初始化运算符栈OPTR，并压入#作为表达式的起始标记
    InitStack(OPTR); 
    Push(OPTR, '#');
    
    // 初始化运算数栈OPND，从输入流读取第一个字符
    InitStack(OPND); 
    c = getchar();
    
    // 循环处理：当输入字符不是#或运算符栈顶不是#时继续
    // 直到表达式处理完毕（#匹配#）
    while (c != '#' || GetTop(OPTR) != '#') {
        // 判断当前字符是否为非运算符（如数字或字母）
        if (!In(c, OP))
        {
            // 非运算符则压入运算数栈，并读取下一个字符
            Push(OPND, c); 
            c = getchar();
        } 
        // 若为运算符，则根据优先级进行处理
        else
            // Precede函数：比较栈顶运算符与当前运算符的优先级
            switch (Precede(GetTop(OPTR), c)) {
                // 栈顶运算符优先级低：当前运算符入栈，读取下一个字符
                case '<': 
                    Push(OPTR, c); 
                    c = getchar(); 
                    break;
                // 优先级相等（如括号匹配或#与#匹配）：弹出栈顶运算符，读取下一个字符
                case '=': 
                    Pop(OPTR, x); 
                    c = getchar(); 
                    break;
                // 栈顶运算符优先级高：弹出栈顶运算符进行计算
                case '>': 
                    Pop(OPTR, theta);       // 弹出运算符theta
                    Pop(OPND, b);           // 弹出右操作数b
                    Pop(OPND, a);           // 弹出左操作数a
                    // 计算a theta b的结果并压入运算数栈
                    Push(OPND, Operate(a, theta, b)); 
                    break;
            }
    }
    // 循环结束时，运算数栈顶即为表达式的计算结果
    return GetTop(OPND);
}

栈与递归的实现

递归函数：类似于多个函数的嵌套调用，只是调用函数和被调用函数是同一个函数。

以下三种情况常常用到递归

• 递归定义的数学函数：如阶乘函数\(Fact(n)=\begin{cases} 1 & 若n = 0 \\ n * Fact(n – 1) & 若n > 0 \end{cases}\)
• 具有递归特性的数据结构：如二叉树、广义表
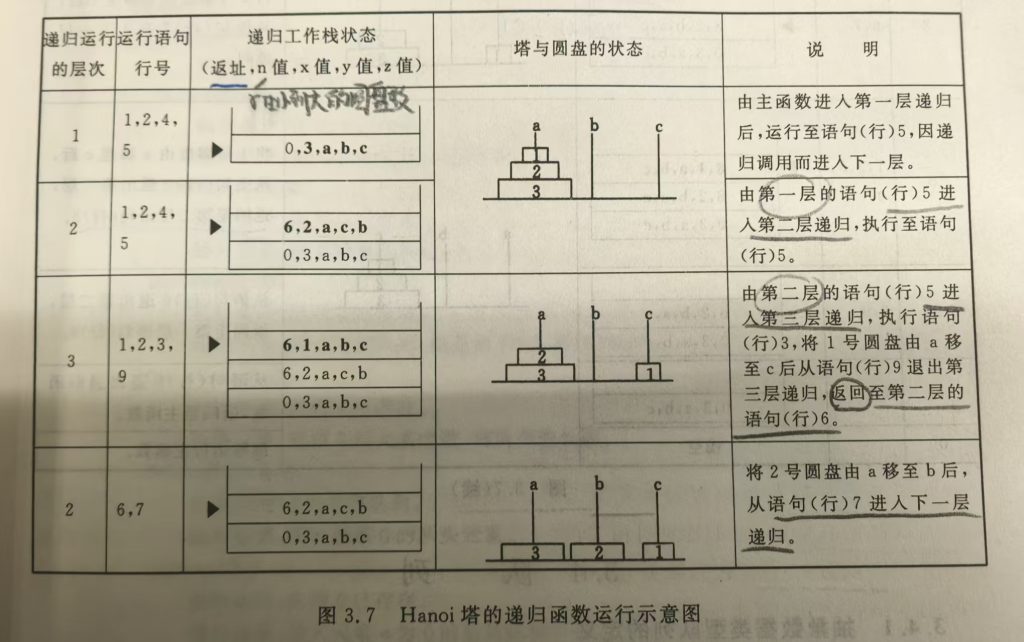
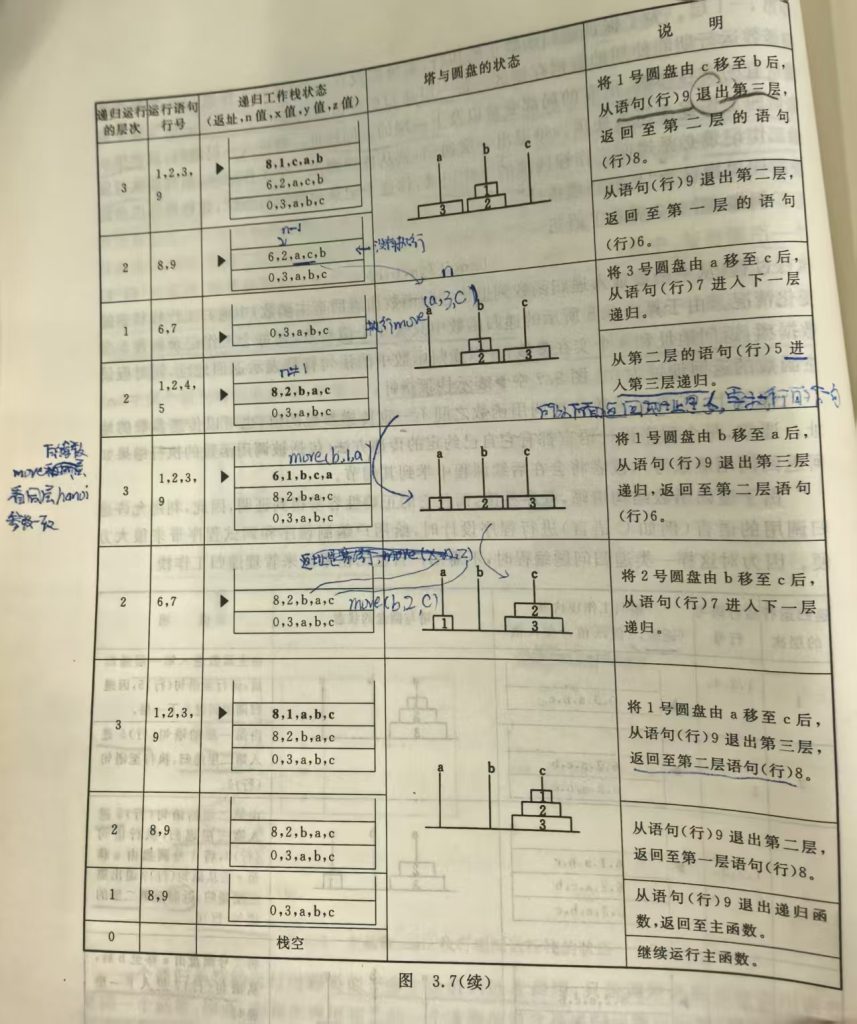
• 可递归求解的问题：如八皇后问题，Hanoi 塔问题

递归问题—用分治法求解
分治法：对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解

函数调用过程：
调用前，系统完成：

将实参、返回地址等传递给被调用函数
为被调用函数的局部变量分配存储区
将控制转移到被调用函数的入口

调用后，系统完成：

保存被调用函数的计算结果
释放被调用函数的数据区
依照被调用函数保存的返回地址将控制转移到调用函数

遵循后调用的先返回

队列 (Queue)

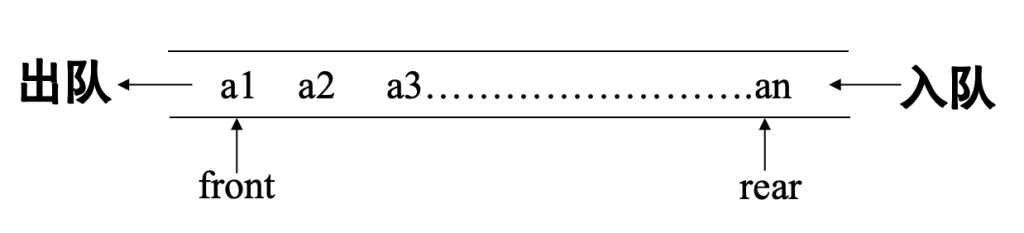
只能在队尾进行插入，在对头进行删除的线性表
先进先出 FIFO

逻辑结构：同线性表相同，仍为一对一关系
存储结构：顺序队或链队，以循环顺序队列更常见

队列的常见应用：脱机打印输出：按申请的先后顺序依次输出…

队列的抽象数据类型定义

ADT Queue {

数据对象：\(D=\{a_i | a_i \in \text{ElemSet}, i = 1,2 \dots n, n\geq0\}\)

数据关系：\(R1 = \{< a_{i - 1}, a_i > | a_{i - 1}, a_i \in D\}\)

约定\(a_1\)端为队列头，\(a_n\)端为队列尾

基本操作：

InitStack (&Q)；DestroyStack (&Q);

EnQueue (&Q, e); DeQueue (&Q, &e);

…… 等等

} ADT Queue

• InitQueue(&Q)：
  • 操作结果：构造一个空队列 Q
• DestroyQueue (&Q)
  • 初始条件：队列 Q 已经存在
  • 操作结果：销毁队列 Q
• ClearQueue (&Q)
  • 初始条件：队列 Q 已经存在
  • 操作结果：将队列 Q 清为空队列
• QueueEmpty(Q)：
  • 初始条件：队列 Q 已经存在
  • 操作结果：若队列 Q 为空队列，返回 TURE；否则返回 FALSE
• QueueLength (Q)
  • 初始条件：队列 Q 已经存在
  • 操作结果：返回队列 Q 中的元素个数，即队列的长度
• GetHead (Q, &e)
  • 初始条件：队列 Q 已经存在且非空
  • 操作结果：用 e 返回队列 Q 的队头元素

• EnQueue(&Q, e)：
  • 初始条件：队列 Q 已经存在
  • 操作结果：插入元素 e 为新的队尾元素
• DeQueue (&Q, &e)
  • 初始条件：队列 Q 已经存在且非空
  • 操作结果：删除 Q 的队头元素，并用 e 返回其值
• QueueTraverse(Q, visit())
  • 初始条件：队列 Q 已经存在且非空
  • 操作结果：从队头到队尾依次对 Q 的每个数据元素调用函数 visit ()，一旦 visit () 失败，则操作失败。

队列的表示和实现

由于队列本身就是线性表，也有顺序存储和链式存储两种实现方式
队列的顺序存储—顺序队列
队列的链式存储—链队列（循环队列）

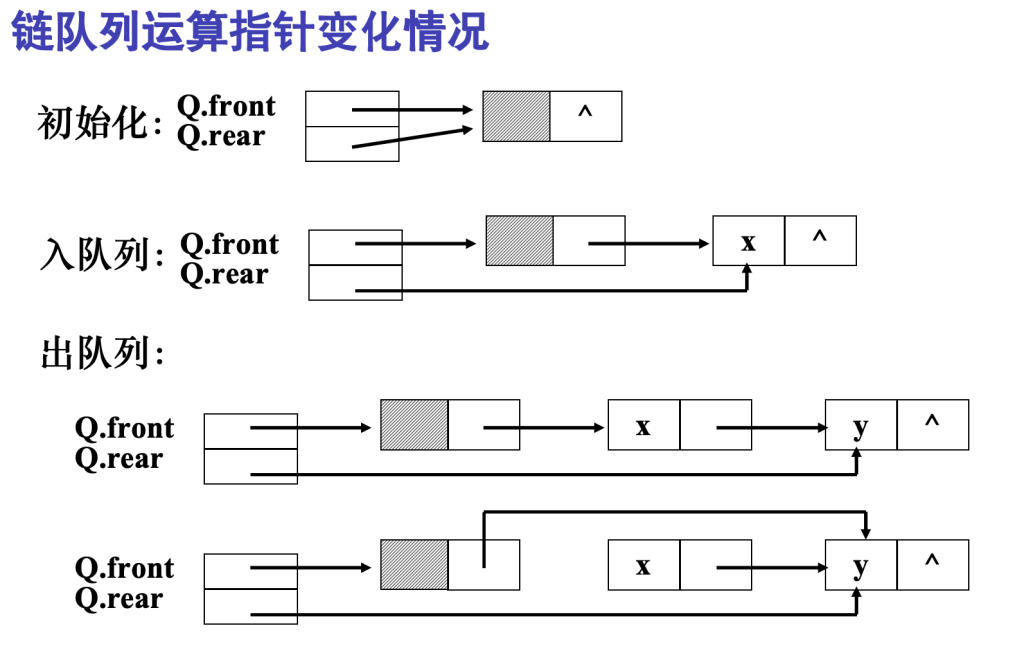
//链队列的操作-初始化
Status InitQueue (LinkQueue &Q)
{ Q.front=Q.rear= (QueuePtr) malloc (sizeof (QNode));
  if (! Q.front) exit (OVERFLOW);
  Q.front ->next = NULL;
  return OK;
}

//链队列的操作 - 销毁链队列
//思想：从队头结点开始，依次释放所有节点
Status DestroyQueue (LinkQueue &Q)
{ while (Q.front) {
    Q.rear = Q.front -> next;
    Free (Q.front);
    Q.front = Q.rear;
  }
  return OK;
}

链队列的操作 - 入队列
Status EnQueue (LinkQueue &Q, QElemType e)
{ p = (QueuePtr) malloc (sizeof (QNode));
  if (! p) exit (OVERFLOW);
  p -> data = e; p -> next = NULL;
  Q.rear -> next = p;
  Q.rear = p;
  return OK;
}

链队列的操作 - 出队列
Status DeQueue (LinkQueue &Q, QElemType &e)
{ if (Q.front == Q.rear) return ERROR;
  p = Q.front -> next;
  e = p -> data;
  Q.front ->next = p -> next;
  if (Q.rear == p) Q.rear = Q.front;
  free (p);
  return OK;
}

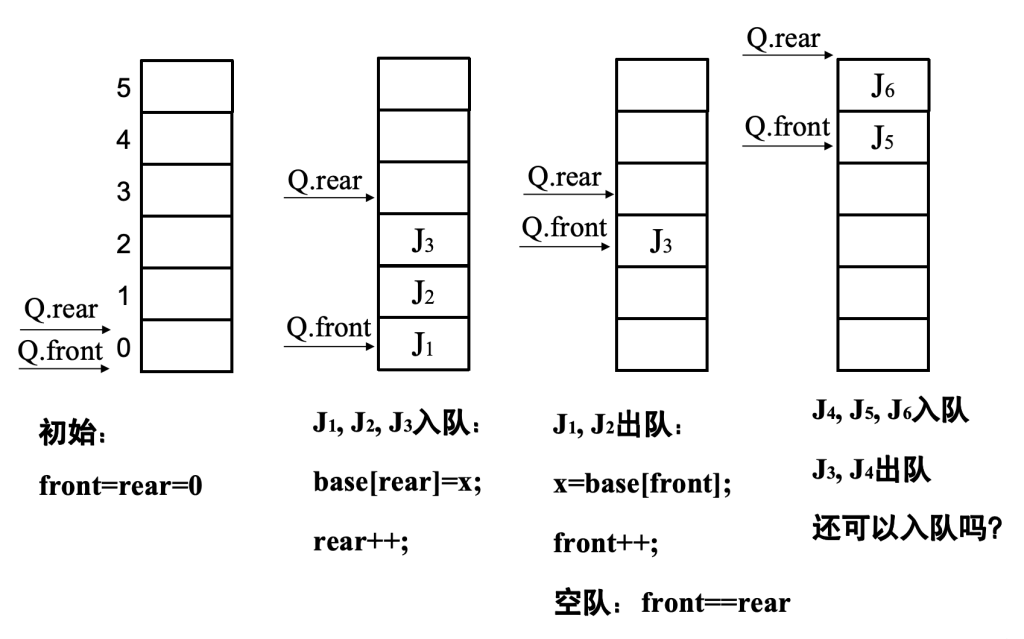
环状队列

若以最后图像的状态，不可再继续插入新的队尾元素因为数组越界，然而此时不宜如顺序栈那样扩大数组空间，因为队列的实际可用空间被没有占满，一个巧妙的方法是将顺序队列臆造为一个环状的空间，称之为环状队列

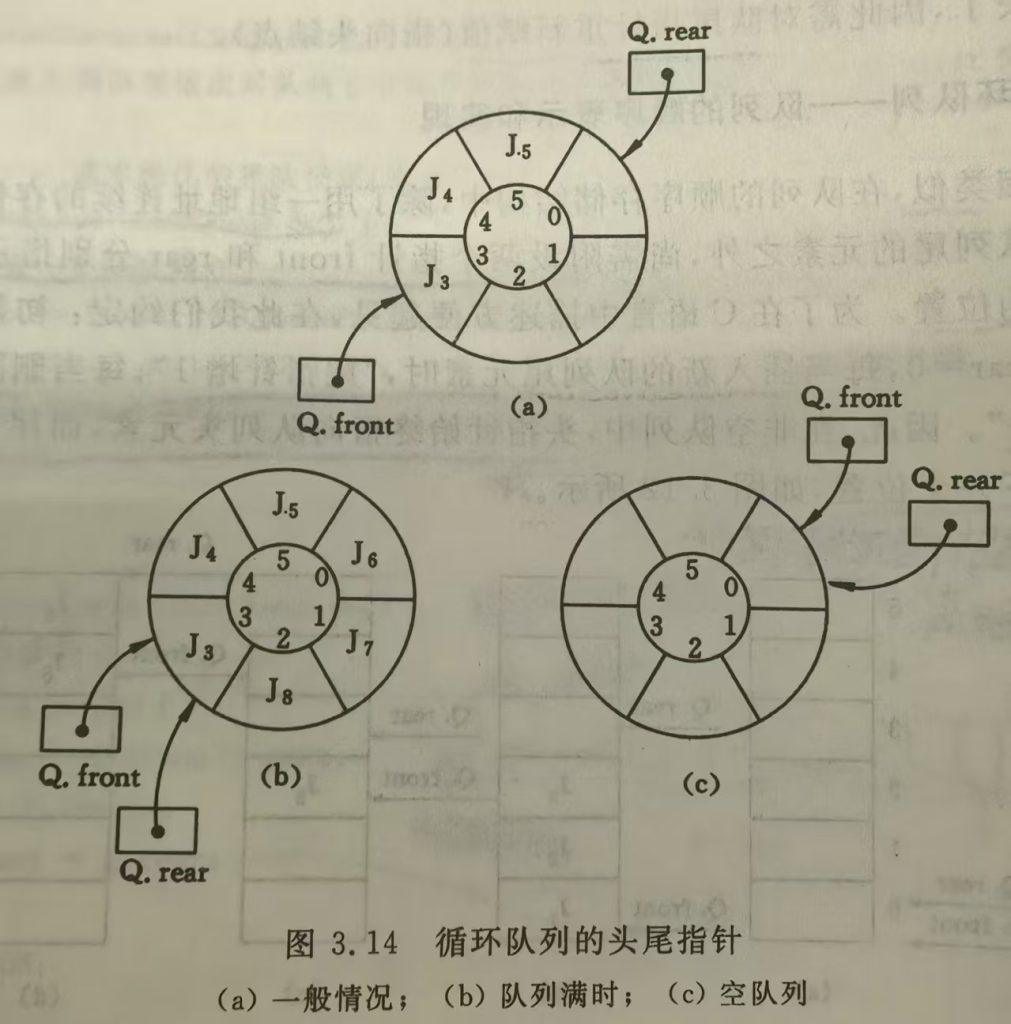
循环队列-队满和队空无法区分问题？
另外设一个标志区分队空队满
少用一个元素空间，以尾指针加1等于头指针作为队列满的标志，即队列满的条件:
( Q.rear + 1 )%MAXQSIZE = Q.front

循环队列的基本操作-初始化

Status InitQueue (SqQueue &Q)
{Q.base=(QElemType *)malloc(MAXQSIZE*sizeof(QElemType));
  if (! Q.base ) exit (OVERFLOW);
  Q.front = Q.rear = 0;
  return OK;
}

循环队列的基本操作 – 入队列

Status EnQueue (SqQueue &Q, QElemType e)
{ if ((Q.rear+1)% MAXQSIZE == Q.front ) return ERROR;
  Q.base [ Q.rear ] = e;
  Q.rear = ( Q.rear + 1 ) % MAXQSIZE;
  return OK;
}

循环队列的基本操作 – 出队列

Status DeQueue (SqQueue &Q, QElemType &e)
{ if ( Q.front == Q.rear ) return ERROR;
  e = Q.base [ Q.front ];
  Q.front = ( Q.front + 1 ) % MAXQSIZE;
  return OK;
}

例题：

3.15 假设以顺序存储结构实现一个双向栈，即在一维数组的存储空间中存在着两个栈，它们的栈底分别设在数组的两个端点。试编写实现这个双向栈 tws 的三个操作：初始化 inittack(tws)、入栈 push(tws,i,x) 和出栈 pop(tws,i) 的算法，其中 i 为 0 或 1，用以分别指示设在数组两端的两个栈，并讨论按过程(正/误状态变量可设为零参)或函数设计这些操作算法各有什么有缺点。

1. 标准共享栈（两端向中间生长）

这是最经典的共享栈模型，核心特点：

• 栈底位置：
  • 栈 1 的栈底在数组起始位置（base1 = arr[0]）。
  • 栈 2 的栈底在数组末尾位置（base2 = arr[size-1]）。
• 生长方向：
  • 栈 1 的栈顶 top1 从栈底（起始位置）向中间移动（入栈时 top1++）。
  • 栈 2 的栈顶 top2 从栈底（末尾位置）向中间移动（入栈时 top2--）。
• 栈满条件：top1 + 1 == top2（两个栈顶 “相邻”，中间无剩余空间）。

2. 此题的变种（中间起始向两端扩展）

代码里的设计是另一种 “共享思路”：

• 初始栈顶：两个栈的栈顶都从数组中间开始（top[0] = top[1] = p + m/2）。
• 生长方向：
  • 栈 0（i=0）向数组起始端扩展（入栈时 top[0]--）。
  • 栈 1（i=1）向数组末尾端扩展（入栈时 top[1]++）。
• 栈满条件：top[0] == p（栈 0 触达起始端）或 top[1] == p + stacksize - 1（栈 1 触达末尾端）。

所以，之前的解释是共享栈的 “变种实现”，和标准 “两端向中间” 模型不冲突，只是栈顶初始位置和扩展方向相反
栈 0 向左、栈 1 向右，因此它们的 “可用空间” 是从中间向两端逐步占用的。当两个栈顶指针 top[0] 和 top[1] 相遇时（top[0] == top[1]），栈为空；当栈 0 的 top[0] 触达数组起点（p），或栈 1 的 top[1] 触达数组末尾（p + stacksize - 1）时，对应栈满

// 双向栈类定义
class DStack {
    // 两个栈顶指针，top[0]对应一个栈，top[1]对应另一个栈
    ElemType *top[2];
    // 指向数组起始位置的指针
    ElemType *p;
    // 栈的总大小
    int stacksize;
    // 用于指示操作的是哪个栈（0或1）
    int di;
public:
    // 构造函数，初始化双向栈，参数m为数组大小
    DStack(int m) {
        // 为数组分配m个ElemType类型的空间
        p = new ElemType[m];
        // 如果内存分配失败，退出程序
        if (!p) exit(OVERFLOW);
        // 初始化top[0]为数组中间位置，作为其中一个栈的栈顶初始位置
        top[0] = p + m / 2;
        // 初始化top[1]与top[0]相同，作为另一个栈的栈顶初始位置
        top[1] = top[0];
        // 设置栈的总大小
        stacksize = m;
    }
    // 析构函数，释放数组内存
    ~DStack() { delete p; }
    // 入栈操作，i指示栈（0或1），x为入栈元素
    void Push(int i, ElemType x) {
        // 记录要操作的栈
        di = i;
        // 操作第0个栈
        if (di == 0) {
            // 由中间向左扩展，栈顶不断减小。如果栈顶指针大于数组起始指针，说明栈未满，可入栈
            if (top[0] > p) 
                //先赋值再自减
                *top[0]-- = x;
            else 
                cerr << "Stack overflow!";
        } else {
            // 操作第1个栈，由中间向右扩展，栈顶不断自增
            // 如果栈顶指针小于数组末尾指针，说明栈未满，可入栈
            if (top[1] < p + stacksize - 1) 
                *++top[1] = x;
            else 
                cerr << "Stack overflow!";
        }
    }
    // 出栈操作，i指示栈（0或1），返回出栈元素
    ElemType Pop(int i) {
        // 记录要操作的栈
        di = i;
        // 操作第0个栈
        if (di == 0) {
            // 如果两个栈顶指针不重叠，说明栈非空，可出栈
            if (top[0] < top[1]) 
                return *++top[0];
            else 
                cerr << "Stack empty!";
        } else {
            // 操作第1个栈，如果两个栈顶指针不重叠，说明栈非空，可出栈
            if (top[1] > top[0]) 
                return *top[1]--;
            else 
                cerr << "Stack empty!";
        }
        return 0;
    }
};

橙色子索引问题：
假设数组 p 的总大小为 stacksize（即能存储 stacksize 个元素），那么数组的有效索引范围是 0 到 stacksize - 1（从起始位置到末尾位置）。

p + stacksize - 1 指向数组的最后一个有效位置（索引 stacksize - 1 对应的位置）。

p 指向数组的起始地址（索引 0 对应的位置）。

// 计算 Ackerman 函数的递归算法
int akm(int m, int n) {
    // 当 m 为 0 时，直接返回 n + 1
    if (m == 0) {
        return n + 1;
    } 
    // 当 m 不为 0 但 n 为 0 时，递归调用 akm(m - 1, 1)
    else if (n == 0) {
        return akm(m - 1, 1);
    } 
    // 当 m 和 n 都不为 0 时，递归调用 akm(m - 1, akm(m, n - 1))
    else {
        return akm(m - 1, akm(m, n - 1));
    }
}

非递归实现 Ackerman 函数的核心思路是用栈模拟递归调用的过程，因为递归的本质是函数调用栈的层层嵌套，用自定义的栈可以手动管理这些 “调用” 与 “返回” 逻辑。

栈的作用：用栈来存储待计算的 Ackerman 函数参数（m 和 n）。每次处理栈顶的参数，根据 Ackerman 函数的定义，将复杂的递归分解为更简单的子问题，逐步推进计算，直到能直接得到结果。

// 非递归算法：计算 Ackerman 函数
int akm1(int m, int n)
{
    // 定义栈 s，用于模拟递归调用栈
    Stack s;
    // 初始化栈
    InitStack(s);
    // 定义结构体变量 e, e1, d，用于存储 Ackerman 函数的参数 m 和 n
    ElemType e, e1, d;
    // 初始化当前要计算的 Ackerman 函数参数 m 和 n
    e.mval = m;     
    e.nval = n;
    // 将初始参数入栈
    Push(s, e);
    do {
        // 当 m 不为 0 时，进入循环处理
        while (e.mval) {
            // 当 n 不为 0 时，进入循环处理
            while (e.nval) {
                // n 减 1
                e.nval--;
                // 将新的参数入栈
                Push(s, e);
            }
            // m 减 1，n 置为 1
            e.mval--; e.nval = 1;
        }
        // 如果栈中元素个数大于 1，进行回溯计算
        if (StackLength(s) > 1) {
            // 保存当前栈顶元素的 n 值
            e1.nval = e.nval;
            // 弹出栈顶元素
            Pop(s, e);
            // m 减 1
            e.mval--;
            // n 为子问题结果加 1
            e.nval = e1.nval + 1;
        }
    // 直到栈中只剩一个元素且 m 为 0（此时可直接计算结果）
    } while (StackLength(s) != 1 || e.mval != 0);
    // 返回最终结果（结果为 nval + 1，因为 m 为 0 时结果是 n + 1）
    return e.nval + 1;
}

3.19 假设一个算术表达式中可以包含三种括号：圆括号 “(” 和 “)”、方括号 “[” 和 “]” 和花括号 “{” 和 “}”，且这三种括号可按任意的次序嵌套使用（如：…[…{…}…[… ]…]…[… ]…(…)…）。编写判别给定表达式中所含括号是否正确配对出现的算法（已知表达式已存入数据元素为字符的顺序表中）

def is_bracket_matched(expr):
    stack = []
    # 定义括号匹配的字典，右括号为键，左括号为值
    bracket_map = {')': '(', ']': '[', '}': '{'}
    for char in expr:
        if char in '([{':  # 左括号入栈
            stack.append(char)
        elif char in ')]}':  # 右括号判断匹配
            if not stack:  # 栈空，无左括号匹配
                return False
            top = stack.pop()
            if bracket_map[char] != top:  # 左右括号不匹配
                return False
    return len(stack) == 0  # 栈空则全部匹配

# 测试示例
expr1 = "3+[4*(5-2)]"
expr2 = "3+[4*(5-2)"
expr3 = "3+[4*(5-2)}"

print(f"表达式 '{expr1}' 括号匹配：{is_bracket_matched(expr1)}")
print(f"表达式 '{expr2}' 括号匹配：{is_bracket_matched(expr2)}")
print(f"表达式 '{expr3}' 括号匹配：{is_bracket_matched(expr3)}")

3.28 假设以带头结点的循环链表表示队列，并且只设一个指针指向队尾元素结点（注意不设头指针），试编写相应的队列初始化、入队列和出队列的算法。

// 定义元素类型为 int
typedef int ElemType;
// 定义链表结点结构
typedef struct NodeType {
    ElemType data;
    struct NodeType *next;
} QNode, *QPtr;
// 定义队列结构，包含队尾指针和队列大小
typedef struct {
    QPtr rear;
    int size;
} Queue;

// 队列初始化函数
Status InitQueue(Queue &q) {
    // 队尾指针初始化为 NULL
    q.rear = NULL;
    // 队列大小初始化为 0
    q.size = 0;
    return OK;
}

// 入队列函数，将元素 e 加入队列
Status EnQueue(Queue &q, ElemType e) {
    QPtr p;
    // 分配新结点内存
    p = new QNode;
    if (!p) return FALSE;
    // 新结点数据域赋值为 e
    p->data = e;
    // 若队列为空
    if (!q.rear) {
        // 队尾指针指向新结点
        q.rear = p;
        // 新结点的 next 指向自己，形成循环
        p->next = q.rear;
    } else {
        //若队列非空
        // 新结点的 next 指向队头（原队尾的 next）
        p->next = q.rear->next;
        // 原队尾的 next 指向新结点
        q.rear->next = p;
        // 队尾指针指向新结点
        q.rear = p;
    }
    // 队列大小加 1
    q.size++;
    return OK;
}

// 出队列函数，将队头元素出队并保存到 e 中
Status DeQueue(Queue &q, ElemType &e) {
    QPtr p;
    // 若队列为空，出队失败
    if (q.size == 0) return FALSE;
    // 若队列只有一个元素
    if (q.size == 1) {
        // 将指针 p 指向这个唯一的结点，后续对该结点进行数据获取和内存释放操作
        p = q.rear;
        // 取出结点数据
        e = p->data;
        // 队尾指针置为 NULL
        q.rear = NULL;
        // 释放结点内存
        delete p;
    } else {
        // p 指向队头结点（队尾的 next 指向队头）
        p = q.rear->next;
        // 取出队头结点数据
        e = p->data;
        // 队尾的 next 指向新的队头（原队头的 next）
        q.rear->next = p->next;
        // 释放原队头结点内存
        delete p;
    }
    // 队列大小减 1
    q.size--;
    return OK;
}

算法思路

• 初始化队列（InitQueue）：将队尾指针 rear 置为 NULL，表示队列为空，同时将队列大小 size 初始化为 0。
• 入队列（EnQueue）：首先创建新结点存储要入队的元素。若队列为空，新结点成为队尾，且自身形成循环（next 指向自己）；若队列非空，新结点插入到队尾，调整队尾指针 rear 指向新结点，并维护循环链表的结构，最后队列大小加 1。
• 出队列（DeQueue）：先判断队列是否为空，若为空则出队失败。若队列只有一个元素，取出该元素，释放结点并将队尾指针置为 NULL；若队列有多个元素，找到队头元素（通过队尾指针的 next 找到），取出元素，调整链表结构，释放队头结点，最后队列大小减 1。

3.30 假设将循环队列定义为：以域变量 rear 和 length 分别指示循环队列中队尾元素的位置和内含元素的个数。试给出此循环队列的队满条件，并写出相应的入队列和出队列的算法（在出队列的算法中要返回队头元素）

// 定义队列的最大容量
#define MaxQSize 4
// 定义队列中元素的类型为 int
typedef int ElemType;
// 定义循环队列的结构体
typedef struct {
    // 指向存储队列元素的数组的指针
    ElemType *base;
    // 指示队尾元素的位置
    int rear;
    // 队列中内含元素的个数
    int length;
} Queue;

// 初始化队列的函数
Status InitQueue(Queue &q) {
    // 为队列分配 MaxQSize 个 ElemType 类型的空间
    //当将数组名赋值给指针时，数组名会隐式转换为指向数组首元素的指针（即首元素的地址）
    q.base = new ElemType[MaxQSize];
    // 如果分配空间失败，返回 FALSE
    if (!q.base) return FALSE;
    // 初始时队尾位置为 0
    q.rear = 0;
    // 初始时队列中元素个数为 0
    q.length = 0;
    // 初始化成功，返回 OK
    return OK;
}

// 入队列的函数，将元素 e 加入队列
Status EnQueue(Queue &q, ElemType e) {
    // 通过下一个队尾的位置” 是否等于 “队头的位置”判断队列是否已满 
    if ((q.rear + 1) % MaxQSize == (q.rear + MaxQSize - q.length) % MaxQSize)
        // 队满，无法入队，返回 FALSE
        return FALSE;
    else {
        // 将元素 e 放入队尾位置
        q.base[q.rear] = e;
        // 队尾位置后移一位，利用取模运算实现循环
        q.rear = (q.rear + 1) % MaxQSize;
        // 队列中元素个数加 1
        q.length++;
    }
    // 入队成功，返回 OK
    return OK;
}

// 出队列的函数，将队头元素出队并保存到 e 中
Status DeQueue(Queue &q, ElemType &e) {
    // 通过通过 “队头位置”是否等于“队尾位置” ，判断队列是否为空
    if ((q.rear + MaxQSize - q.length) % MaxQSize == q.rear)
        // 队空，无法出队，返回 FALSE
        return FALSE;
    else {
        // 计算队头元素的位置，将其值赋给 e
        e = q.base[(q.rear + MaxQSize - q.length) % MaxQSize];
        // 队列中元素个数减 1
        q.length--;
    }
    // 出队成功，返回 OK
    return OK;
}

(q.rear + 1) % MaxQSize：表示下一个队尾的位置。因为rear是当前队尾位置，插入一个新元素后，队尾要后移一位，通过取模运算保证在数组范围内循环。

(q.rear - q.length + MaxQSize) % MaxQSize：表示队头的位置。

• 已知rear是队尾位置，length是元素个数。
• 队列中元素是连续存储的（循环意义上的连续），所以队头位置 = 队尾位置 – 元素个数 + 最大容量（取模是为了防止负数，保证在数组索引范围内）。