
我们希望构造一个多项式 \(p(x)\),满足 \(p(90) = 5.2\)、\(p(105) = 5.9\)、\(p(120) = 7\)、\(p(135) = 8.4\)。但我们该选择多少次多项式呢?尝试使用含 4 个系数的多项式,即:\(p(x) = a_0 + a_1x + a_2x^2 + a_3x^3\)
需要满足的条件为:\(\begin{align*} a_0 + 90a_1 + 90^2a_2 + 90^3a_3 &= 5.2 \\ a_0 + 105a_1 + 105^2a_2 + 105^3a_3 &= 5.9 \\ a_0 + 120a_1 + 120^2a_2 + 120^3a_3 &= 7 \\ a_0 + 135a_1 + 135^2a_2 + 135^3a_3 &= 8.4 \end{align*}\)
这是一个含 4 个未知数的四元一次方程组。若行列式:\(\det\begin{pmatrix} 1 & 90 & 90^2 & 90^3 \\ 1 & 105 & 105^2 & 105^3 \\ 1 & 120 & 120^2 & 120^3 \\ 1 & 135 & 135^2 & 135^3 \end{pmatrix} \neq 0\)
则该线性方程组有唯一解。在完成求解前,我们先考虑一个更简单但更通用的例子
插值多项式Interpolating polynomial
给定互异的 \(x_0, x_1, x_2\),构造一个次数 ≤2 的插值多项式Interpolating polynomial \(p_2(x)\),满足:\(p_2(x_0) = y_0, \quad p_2(x_1) = y_1, \quad p_2(x_2) = y_2\)
构造步骤
- 步骤 1:从点 \(x_0\) 出发,构造一个在另外两点 \(x_1, x_2\) 处为 0 的多项式,利用因式表示为:\(L(x) = (x – x_1)(x – x_2)\)
- 步骤 2:计算该多项式在 \(x_0\) 处的值:\(L(x_0) = (x_0 – x_1)(x_0 – x_2)\)
- 步骤 3:调整 \(L(x)\) 使其在 \(x = x_0\) 处值为 1,即除以 \(L(x_0)\),得到基函数 \(L_0(x)\):\(L_0(x) = \frac{(x – x_1)(x – x_2)}{(x_0 – x_1)(x_0 – x_2)}\) 验证:\(L_0(x_0) = 1\),\(L_0(x_1) = 0\),\(L_0(x_2) = 0\)。
- 步骤 4:对另外两点重复上述过程:
- 对于 \(x_1\),令 \(L(x) = (x – x_0)(x – x_2)\),则 \(L(x_1) = (x_1 – x_0)(x_1 – x_2)\),故:\(L_1(x) = \frac{(x – x_0)(x – x_2)}{(x_1 – x_0)(x_1 – x_2)}\)
- 对于 \(x_2\),令 \(L(x) = (x – x_0)(x – x_1)\),则 \(L(x_2) = (x_2 – x_0)(x_2 – x_1)\),故:\(L_2(x) = \frac{(x – x_0)(x – x_1)}{(x_2 – x_0)(x_2 – x_1)}\)
- 步骤 5:组合基函数得到插值多项式:\(p_2(x) = a_0L_0(x) + a_1L_1(x) + a_2L_2(x)\)
- 步骤 6:确定系数 \(a_0, a_1, a_2\):
- 当 \(x = x_0\) 时,\(p_2(x_0) = a_0L_0(x_0) + a_1L_1(x_0) + a_2L_2(x_0) = a_0 \times 1 + a_1 \times 0 + a_2 \times 0 = a_0\),故 \(a_0 = y_0\);
- 同理,\(a_1 = y_1\),\(a_2 = y_2\)。最终:\(p_2(x) = y_0L_0(x) + y_1L_1(x) + y_2L_2(x)\) 注意:通常无需展开乘积项。
拉格朗日插值基函数 \(L_0(x)\)
示例:次数≤3 的多项式
已知 \(x_0, x_1, x_2\) 和 \(x_3\) 均互不相同,且已知 \(y_0, y_1, y_2\) 和 \(y_3\),求 \(p_3(x)\),即次数≤3 的多项式,使得 \(p_3(x_i) = y_i, \quad i = 0,1,2,3\)
设 \(L_0(x), L_1(x), L_2(x)\) 和 \(L_3(x)\) 为次数≤3 的多项式,满足
\(\begin{array}{c|cccc} x & x_0 & x_1 & x_2 & x_3 \\ \hline L_0(x) & 1 & 0 & 0 & 0 \\ L_1(x) & 0 & 1 & 0 & 0 \\ L_2(x) & 0 & 0 & 1 & 0 \\ L_3(x) & 0 & 0 & 0 & 1 \\ \end{array}\)
即 \(L_j(x_i) = \begin{cases} 1, & i = j \\ 0, & i \neq j \end{cases}\) ,这里是在介绍拉格朗日插值基多项式,用于构造满足插值条件的三次(及以下)插值多项式 。
要构造 \(L_0(x)\),我们需要像之前那样考虑因式。当 \(x = x_1, x_2, x_3\) 时,\(L_0(x) = 0\),因此我们可以先临时定义 \(L(x)\) 为:
\(L(x) = (x – x_1)(x – x_2)(x – x_3)\)
现在看 \(L(x_0)\) 的值:
\(L(x_0) = (x_0 – x_1)(x_0 – x_2)(x_0 – x_3)\)
为了让 \(L_0(x_0) = 1\),我们需要定义:
\(\begin{align*} L_0(x) &= \frac{L(x)}{L(x_0)} \\ &= \frac{(x – x_1)(x – x_2)(x – x_3)}{(x_0 – x_1)(x_0 – x_2)(x_0 – x_3)} \\ &= \prod_{k = 1}^{3} \frac{x – x_k}{x_0 – x_k} = \prod_{\substack{k = 0 \\ k \neq 0}}^{3} \frac{x – x_k}{x_0 – x_k} \end{align*}\)
类似地
\(\begin{align*} L_1(x) &= \prod_{\substack{k = 0 \\ k \neq 1}}^{3} \frac{x – x_k}{x_1 – x_k} \\ L_2(x) &= \prod_{\substack{k = 0 \\ k \neq 2}}^{3} \frac{x – x_k}{x_2 – x_k} \\ L_3(x) &= \prod_{\substack{k = 0 \\ k \neq 3}}^{3} \frac{x – x_k}{x_3 – x_k} \end{align*}\)
一般地
\(L_j(x) = \prod_{\substack{k = 0 \\ k \neq j}}^{3} \frac{x – x_k}{x_j – x_k}, \quad j = 0,1,2,3\)
最后
\(p_3(x) = y_0L_0(x) + y_1L_1(x) + y_2L_2(x) + y_3L_3(x)\)
呈现了拉格朗日插值基函数 \(L_j(x)\) 的一般形式,以及通过基函数线性组合 \(y_jL_j(x)\) 得到满足插值条件的三次插值多项式 \(p_3(x)\) 的过程 ,属于数值分析中插值法的内容
举例:


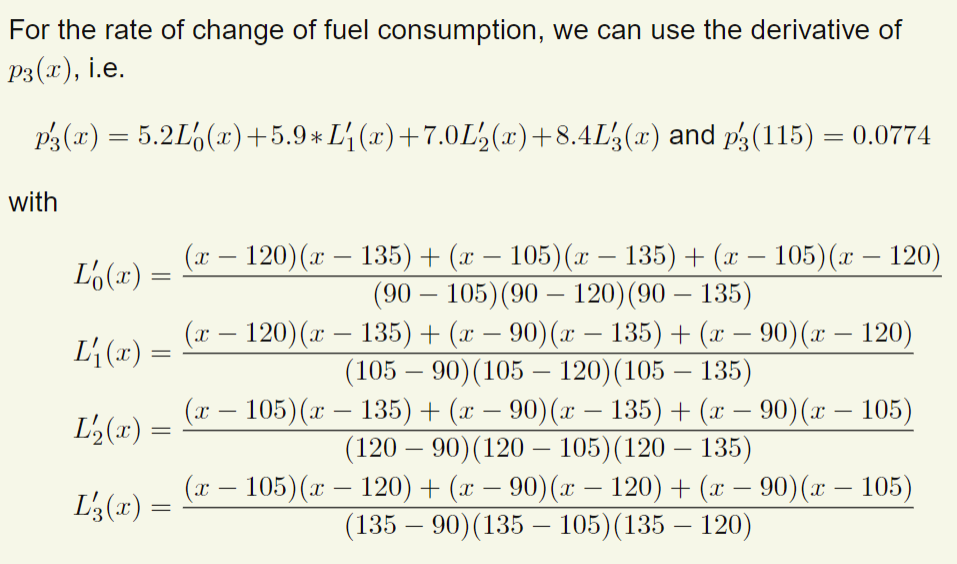
例2:










