Reference:
【数值计算方法】常微分方程初值问题的数值解 – FE-有限元鹰 – 博客园
前置知识:
函数上标的_代表该函数为预估函数,在机器学习中有提到
初值问题与数值解
求微分方程满足初始条件的特解问题称为初值问题。然而初值问题并不是总有解析解,事实上很多函数的原函数的很难求得,所以我们求数值解,通过计算y(t)在节点tn处的近似值yn。
比如想直到满足某初始条件的人口增长模型tn年之后大约有多少人,如果满足该模型的微分方程没有解析解,我们只需要计算其在tn处的数值解即可

之所以称为”一阶”,是因为方程中最高阶导数为一阶;称为”标量”,因为仅涉及单个函数 y。
数值解即求初值问题在节点处函数值的近似
微分方程的近似解法,常用的有欧拉法、改进的欧拉法与龙格—库塔法,而其本质都是将初值问题方程离散化,所以也称为初值问题的数值积分方法
欧拉法
将区间 \([0, T]\) 作 \(N\) 等分,每一小区间长度 \(h = \frac{T}{N}\) 称为步长,\(t_n = nh\) 称为节点。根据初值 \(y(0) = y_0\),代入微分方程可直接解出 \(t = t_0\) 的导数值 \(y’ = f(y_0, t_0)\)。之后再进行迭代最终求得 \(y\)\[
t_{k+1} = t_k + h
\]\[
y_{k+1} = y_k + hf(y_k, t_k)
\]
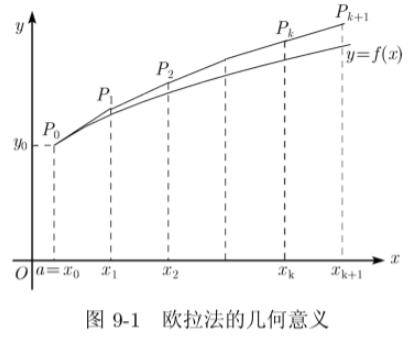
欧拉方法就是用从 P0出发的折线 P0,P1⋅⋅⋅PN 来作为积分曲线 y = y(x) 的近似解,
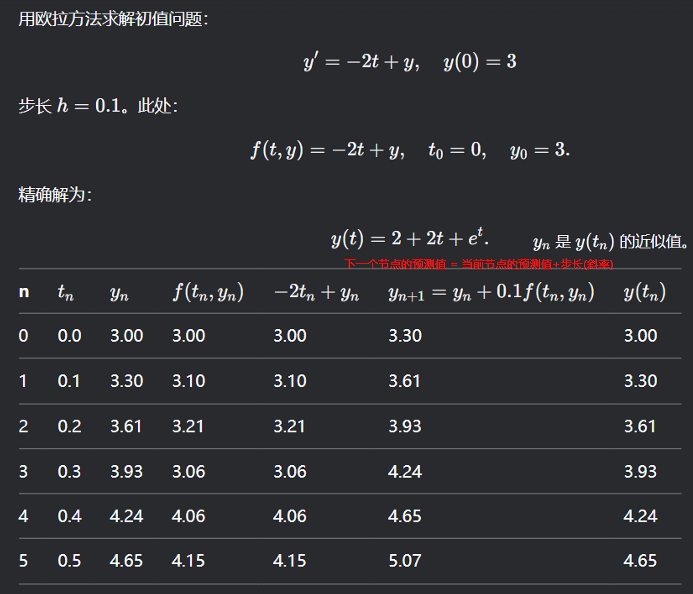
例题


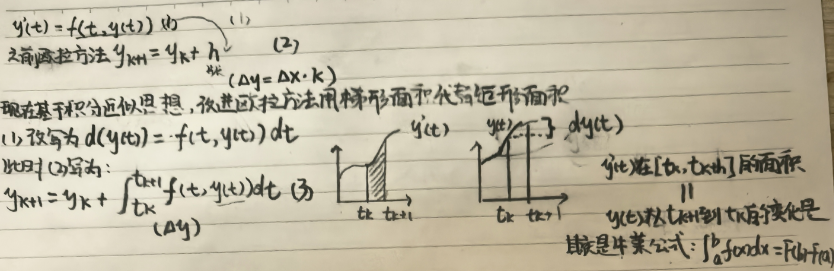
改进的欧拉方法-预估校正法
欧拉法计算的是以f(yk,tk)为高的矩形面积,而改进的欧拉法计算的是图中所示的改进的左梯形数值积分的面积。提到面积我们先将欧拉法的公式写为积分的形式:
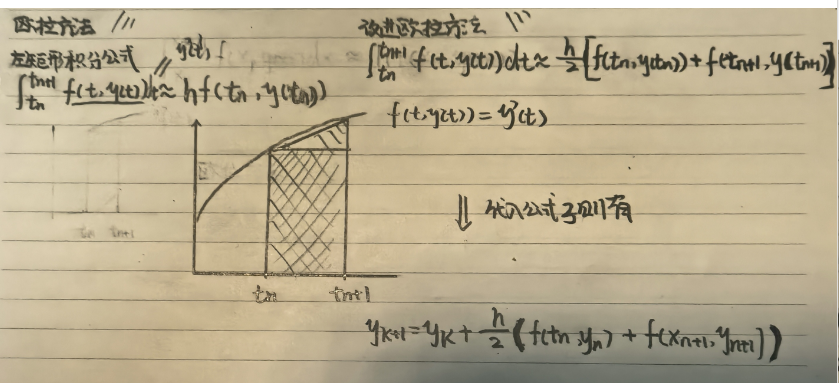
积分式子中含有位置函数y(t)是我们无法求得解析解的方程,采用数值积分的方法计算其近似值,左侧为上述的欧拉法,右侧为改进的欧拉法(梯形公式)
在步长合理时,显然左梯形的面积更接近实际函数下方面积,故改进的欧拉法实际上效果好于欧拉法,但计算量会复杂很多。一种有效简化计算的方法是:当 $h$ 较小时,先使用显式格式计算合适的预估值 $y_{n+1}$,后利用隐式格式迭代一次计算校正值 $y_{n+1}$,称为预估校正方法。下为一阶预估二阶矫正公式
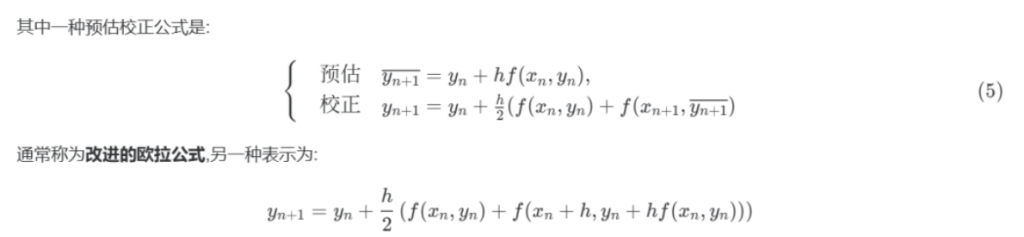
构造预估校正格式时 , 应该注意阶数的匹配, 例如在式 (5) 中 , 校正公式具有二阶精度 , 而预估公式仅具有一阶精度 . 因为提供的预估精度较差 , 且仅经一次校正 , 校正值的精度不会太高
例题


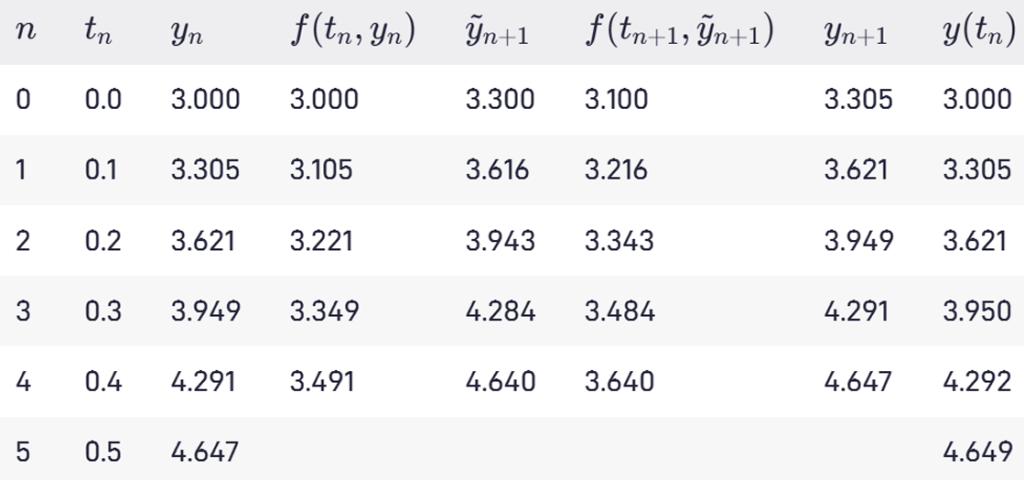
\( O(h^p) \) 的含义
数值方法中常用大O符号描述误差随步长 h变化的速率,\( O(h^2) \) 读作“大O \( h^2 \)”或“\( h^2 \)”阶项。P为误差阶数,指明步长变化时,误差的变化的几何倍数(注意与编程中的时间复杂度区分,其n是趋于无穷大,而这里的h趋于无穷小)
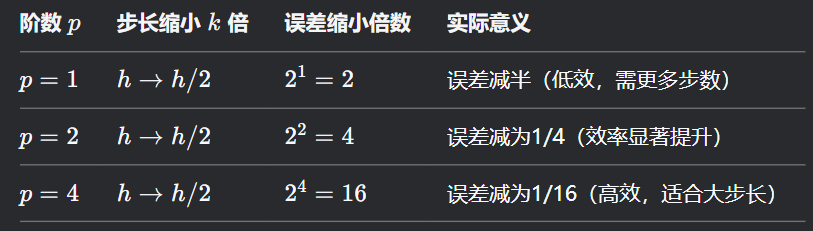
\( O(h^2) \) 标准定义:“当 \( h \to 0 \) 时,某项的幅度(magnitude)增长不超过常数 \( C \) 倍的 \( h^2 \)”。即
\[A = O(h^2)\]表示存在常数 \( C \),使得:
\[|A| \leq Ch^2 \quad (h \to 0).\] 意味:A缩小倍数是h缩小倍数的 p 次方
通常不关心 \( C \) 的具体值。因为即使C很大(比如 C=1000),只要 h足够小,也会让模长变得微不足道。在O用于表示误差大小的语境中,O(h2)表示“误差随 h的平方减小”,这也符合采样的规律的,样本数越多,采样越真实
误差分析
误差类型
- 截断误差:由截断数学过程(如忽略高阶项)引起的误差。
- 舍入误差:由数值的有限精度表示引起的误差。
- 局部误差:单步方法中的误差。
- 全局误差:多步方法应用后的累积误差。
组合可以得到局部截断误差和全局截断误差
局部截断误差衡量数值方法在单一步骤中的近似精度,假设前一步的数值解是精确的,即\( y_n = y(x_n) \),称 \( R_{n+1} = y(x_{n+1}) – y_{n+1} \) 为局部截断误差
对于一般的一步数值方法:\[y_{n+1} = y_n + h f(t_n, y_n,),\]
全局误差表示从初始时刻到当前时刻所有步骤的误差累积结果,定义为精确解与数值解在 \( t_n \) 处的差值:\[E_n = y(t_n) – y_n,\]
龙格 – 库塔公式( R-K 方法)
龙格-库塔算法与欧拉法和改进欧拉法类似,其形式为
\[ y_{n+1} = y_n + \text{对积分} \int_{t_n}^{t_{n+1}} f(t, y(t)) \, dt \]的近似值
不同于欧拉法用矩形面积、改进欧拉法用梯形面积近似积分,龙格-库塔法用 f(x,y) 在某些点上的函数值的线性组合构造近似计算公式 , 再把近似公式和解的泰勒展开式相比较 , 使使前面的若干项吻合 , 从而获得达到一定精度的数值计算公式
龙格 – 库塔公式是一类公式 , 每确定一组特殊的系数 , 就得到一个特殊的龙格 – 库塔公式
二阶R-K公式

4阶R-K公式

n阶RK方法的局部截断误差和全局截断误差和n阶泰勒级数的相同,都分别为O(h^n+1)和O(h^n)
,比如局部截断误差为O(h^5),全局误差为O(h^4)。由全局截断误差为h的n阶无穷小我们知道,当步长足够多的时候,误差趋于0
例题












