用 numpy 表示向量
先在系统中下载numpy库
# 若系统默认 Python 为 3.x
pip install numpy
# 若需明确指定 Python 3
pip3 install numpy
# 若使用 conda 环境
conda install numpy
#若输出版本号则安装成功
python3 -c "import numpy; print(numpy.__version__)"加载numpy库
# 代码示例1:导入numpy库
import numpy as np将两个向量定义为 numpy 数组并打印输出:
# 代码示例2:定义并打印向量
v = np.array([3, -2, 1]) #行向量
b = np.array([[6], [-3], [2.5], [-1], [0]]) #列向量
print('v = ', v, ' and b = ', b)使用 numpy 时,通常无需严格区分行向量与列向量 —— 定义行向量的代码更简洁(输入量更少)。
但在数学表达式中,我们仍会统一使用列向量
用 numpy 实现向量转置
通过 “向量名.T” 表示向量的转置(即数学中的\(b^{T}\)),但输出结果可能与预期略有差异:
# 代码示例4:向量转置(基础用法)
print('v = ', v.T, ' and b = ', b.T)输出结果为:
v = [ 3 -2 1] and b = [[ 6. -3. 2.5 -1. 0. ]]要理解这一结果,需明确:numpy 中的 “向量” 本质是计算机内存中的 “数组”,而非严格的数学向量。若需得到符合数学定义的转置结果,可通过以下方式实现:
# 代码示例5:获取标准列向量转置
v = np.array([[3, -2, 1]]) # 定义为二维数组(行向量形式)
print(v.T) # 转置为列向量输出结果为:
[[ 3]
[-2]
[ 1]]为什么声明为二维数组就可以正常转置向量了
此外,也可通过 “shape 属性” 强制指定数组的维度(即向量的行列数)。代码中的 “#” 用于添加注释,不影响程序运行:
# 代码示例6:通过shape属性调整向量维度
# 定义一个一维数组(本质是数值列表)
a = np.array([3, -2, 1])
print(a) # 打印原始数组
print(a.shape) # 查看数组维度,输出为(3,)(表示1行3列的一维数组)
# 强制将数组维度调整为3行1列(列向量)
a.shape = (3, 1)
print(a) # 打印调整后的列向量
print(a.T) # 打印转置后的行向量输出结果为:
[ 3 -2 1]
(3,)
[[ 3]
[-2]
[ 1]]
[[ 3 -2 1]]以下是另一种定义并转置向量的方法:
# 代码示例7:直接定义行向量并转置为列向量
# 定义1行3列的二维数组(行向量)
b = np.array([[3, -2, 1]])
print(b)
print('The shape of b is ', b.shape) # 查看行向量维度,输出为(1, 3)
# 转置为3行1列的列向量
b = np.array([[3, -2, 1]]).T
print(b)输出结果为:
[[ 3 -2 1]]
The shape of b is (1, 3)
[[ 3]
[-2]
[ 1]]在实际学习中,我们无需过度纠结这些细节 —— 后续将使用的 Python 库会自动处理向量维度的 “记录与匹配” 工作。
用 numpy 实现向量的运算
向量的加法和减法:维度相同的向量可进行加法或减法运算
向量与标量的乘法:向量与标量(单个实数)相乘时,只需将向量的每个分量分别与该标量相乘
# 代码示例8:向量减法与加法
a = np.array([3, -2, 1])
p = np.array([5, 2, -10])
g = a - p # 向量减法
print(g)
a = g + p # 向量加法(验证结果)
print(a)
# 代码示例9:向量与标量的乘法
y = np.array([-3, 16, 1, 1089, 15])
z = -3 * y # 向量与标量(-3)相乘
print(z)输出结果:
[-2 -4 11]
[ 3 -2 1]
[ 9 -48 -3 -3267 -45]向量的范数
“范数”(norm)用于描述 “某个对象的大小”。根据对象类型的不同,“大小” 可能是直观可见的属性,也可能是抽象的度量。向量最直观的 “大小” 度量方式是其 “长度”,我们将先介绍向量的长度(即 2 – 范数),再扩展到更通用的范数定义。
向量的 2 – 范数(\(\ell_{2}\)范数,欧几里得范数或勾股范数)
对于 n 维实数空间中的向量\(v \in \mathbb{R}^{n}\)(其 n 个分量为\(v_{1}, v_{2}, \dots, v_{n}\)),其 “勾股长度”(或 “欧几里得长度”)用2 – 范数表示,计算公式为:
\(\| v \| _{2} = \sqrt{v_{1}^{2} + v_{2}^{2} + \cdots + v_{n}^{2}}\)
从几何角度理解,2 – 范数相当于空间中两点 A 和 B 之间 “直线距离”(即 “两点之间,线段最短” 的距离)
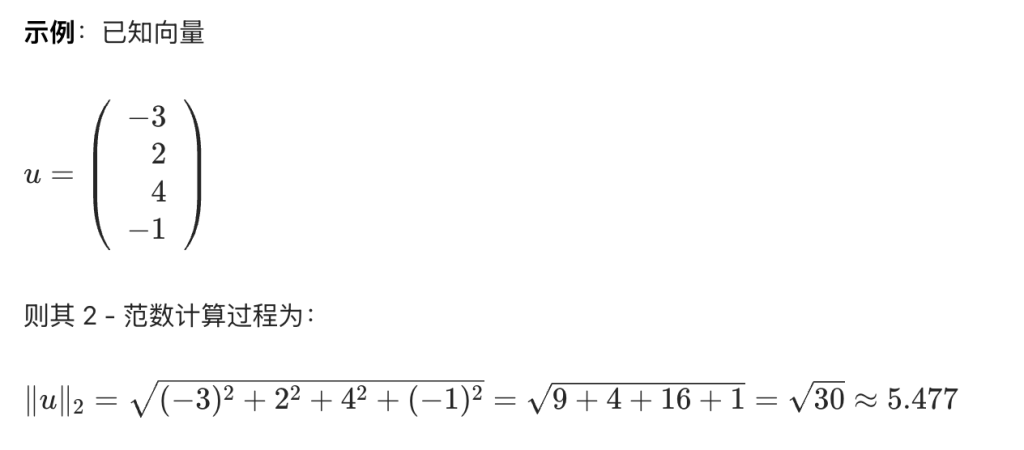
在 numpy 中,可通过 “线性代数子模块”(numpy.linalg)的 “norm 函数” 计算向量范数
# 代码示例10:计算向量的2-范数
u = np.array([-3, 2, 4, -1])
# 方法1:默认计算2-范数
print('||u||_2 = ', np.linalg.norm(u))
# 方法2:显式指定计算2-范数
print('||u||_2 = ', np.linalg.norm(u, 2))
输出结果为:
||u||_2 = 5.477225575051661
||u||_2 = 5.477225575051661向量的 p – 范数(\(\ell_{p}\)范数,闵可夫斯基范数)
在 2 – 范数的基础上,若将 “平方和开平方” 推广为 “p 次方和开 p 次方”,可得到更通用的p – 范数(其中\(p \geq 1\))。其定义为:
\(\| v \| _{p} = \begin{cases} \sqrt[p]{|v_{1}|^{p} + |v_{2}|^{p} + \cdots + |v_{n}|^{p}}, & 1 \leq p < \infty; \\ \max\{ |v_{k}| : k = 1, 2, \dots, n\}, & p = \infty. \end{cases}\)
p – 范数在后续机器学习应用中非常实用,有时也被称为\(\ell_{p}\)范数。
需注意,上述定义中要求\(p \geq 1\)。但在实际应用中,有时会将 p 的取值范围扩展到\(p < 1\),从而得到 “\(\ell_{p}\)范数”(如\(\ell_{1/2}\)范数,记为\(\|v\|_{1/2}\))。但严格来说,当\(p < 1\)时,这些 “范数” 并不满足数学上 “范数” 的严格定义(参考《MML》第 3 章,https://mml-book.github.io),尽管它们在某些场景下仍有实用价值,可称为 “伪范数”(phoney norms)。
一个典型的例子是 **\(\ell_{0}\)范数 **:它表示向量中非零元素的个数。虽然\(\ell_{0}\)范数不满足数学范数的定义,但在 “稀疏性分析”(关注向量中零元素比例)中非常重要。
在所有 p – 范数中,除了前文介绍的欧几里得 2 – 范数,1 – 范数和 ∞- 范数也是实际应用中常用的范数
向量的 1 – 范数(\(\ell_{1}\)范数,曼哈顿范数或出租车范数
1 – 范数常被称为 “曼哈顿距离”,其名称源于二维空间中的几何意义:从点 A 到点 B 的路径只能沿坐标轴方向移动(可呈 “L 形” 或 “阶梯形”)。更多信息可参考维基百科 “出租车几何” 词条:
这种距离类似于在曼哈顿街道网格中行走的方式 —— 无论是步行还是乘坐出租车,都只能沿街道(坐标轴方向)往返,无法直接 “穿街越巷”
向量的∞- 范数(\(\ell_{\infty}\)范数,最大值范数或切比雪夫范数)
∞- 范数并不直接表示两点之间的距离,而是向量所有分量中 “绝对值最大的那个分量的绝对值”。

综合例题:
示例 2:已知向量
\(w = (-19, 18, 2, 0, 0, -8, 34, 0, -57)^{T}\)
则:
- 2 – 范数:\(\| w \| _{2} = \sqrt{(-19)^{2} + 18^{2} + 2^{2} + 0^{2} + 0^{2} + (-8)^{2} + 34^{2} + 0^{2} + (-57)^{2}} = \sqrt{361 + 324 + 4 + 0 + 0 + 64 + 1156 + 0 + 3249} = \sqrt{5158} \approx 71.819\)
- 1 – 范数:\(\| w \| _{1} = 19 + 18 + 2 + 0 + 0 + 8 + 34 + 0 + 57 = 138\)
- ∞- 范数:\(\| w \| _{\infty} = 57\)
- 0 – 范数:\(\| w \| _{0} = 6\)(非零元素个数为 6)
在 numpy 中,可通过指定 norm 函数的第二个参数计算不同类型的范数:
# 代码示例11:计算向量的1-范数、2-范数、∞-范数和0-范数
w = np.array([-19, 18, 2, 0, 0, -8, 34, 0, -57])
print('||w||_2 = ', np.linalg.norm(w, 2)) # 2-范数
print('||w||_1 = ', np.linalg.norm(w, 1)) # 1-范数
print('||w||_inf = ', np.linalg.norm(w, np.inf)) # ∞-范数(用np.inf表示无穷大)
print('||w||_0 = ', np.linalg.norm(w, 0)) # 0-范数
输出结果为:
||w||_2 = 71.8192174839019
||w||_1 = 138.0
||w||_inf = 57.0
||w||_0 = 6.0数据向量化:将数据点表示为向量
# 代码示例12:导入seaborn并查看内置数据集
import seaborn as sns
# 查看所有内置数据集的名称(执行时需按SHIFT+RETURN)
sns.get_dataset_names()
# 代码示例13:加载并查看taxis数据集的前几行
dft = sns.load_dataset('taxis') # dft:data frame taxi(出租车数据集)
dft.head() # 显示数据集的前5行“head ()” 和 “tail ()” 是 pandas 中常用的函数,用于简化数据集的显示(仅展示前几行或后几行)。若直接使用 “print (dft)” 打印整个数据集,输出会非常杂乱,可读性差。
# 代码示例14:打印整个taxis数据集(不推荐,输出过长)
print(dft)
# 代码示例15:用seaborn绘制taxis数据集的散点图(距离vs费用)
sns.scatterplot(data=dft, x="distance", y="fare")
# 代码示例16:绘制散点图(上车区域vs小费)
sns.scatterplot(data=dft, x="pickup_borough", y="tip")数据集的每一行对应一个 “观测值”(如一次出租车行程),包含该观测值的所有特征取值 —— 这正是一个 “数据点”。我们可以通过以下步骤,将一个数据点转换为向量:
首先,查看 taxis 数据集的所有特征名称:
# 代码示例19:查看taxis数据集的特征列名
dft.columns
# 输出结果(特征列表)为:
Index(['pickup', 'dropoff', 'passengers', 'distance', 'fare', 'tip', 'tolls',
'total', 'color', 'payment', 'pickup_zone', 'dropoff_zone',
'pickup_borough', 'dropoff_borough'],
dtype='object')
# 代码示例20:查看taxis数据集的前6行
dft.head(6)为了将数据点转换为向量,我们需要对特征进行筛选和处理:
在 pandas 中,可通过 “iat” 或 “loc+iat” 方法提取数据框中指定位置的元素:
- dft.iat [row_idx, col_idx]:直接通过 “行索引(row_idx)” 和 “列索引(col_idx)” 提取元素(索引从 0 开始)。例如,dft.iat [5,7] 表示提取 “第 6 行第 8 列” 的元素(总费用)。
- dft.loc [row_idx]:提取 “行索引为 row_idx 的整行数据”;dft.loc [row_idx].iat [col_idx]:提取该行中 “列索引为 col_idx 的元素”。
# 代码示例21:提取指定位置的元素并打印
print('dft.iat[5,7] = ', dft.iat[5,7]) # 第6行第8列(总费用)
print('dft.loc[5].iat[7] = ', dft.loc[5].iat[7], '\n') # 同上
print('dft.loc[5] = ')
print(dft.loc[5]) # 打印第6行的所有特征值
输出结果:
dft.iat[5,7] = 12.96
dft.loc[5].iat[7] = 12.96
dft.loc[5] =
pickup 2019-03-11 10:37:23
dropoff 2019-03-11 10:47:31
passengers 1
distance 0.49
fare 7.5
tip 2.16
tolls 0.0
total 12.96
color yellow
payment credit card
pickup_zone Times Sq/Theatre District
dropoff_zone Midtown East
pickup_borough Manhattan
dropoff_borough Manhattan
Name: 5, dtype: object接下来,我们将 “第 3 行(索引为 2)” 的 6 个数值型特征提取出来,组成一个向量:
# 代码示例22:查看taxis数据集的前3行
dft.head(3)
# 代码示例23:方法1:逐个提取数值特征,构建向量
import numpy as np
# 提取第3行(索引2)的6个数值特征:passengers(2)、distance(3)、fare(4)、tip(5)、tolls(6)、total(7)
r3 = np.array([dft.iat[2,2], dft.iat[2,3], dft.iat[2,4], dft.iat[2,5], dft.iat[2,6], dft.iat[2,7]])
print(r3)
输出结果为:
[ 1. 1.37 7.5 2.36 0. 14.16]








