定理内容

从一个总体中，重复很多次地进行这样的操作：
1. 每次随机抽出 n 个样本（比如 100 个）
2. 对每次抽到的样本，求出它们的平均值 \( \bar{X}_1, \bar{X}_2, \bar{X}_3, \dots \)
这样就能得到很多平均值，其构成了一个“样本平均值的分布”
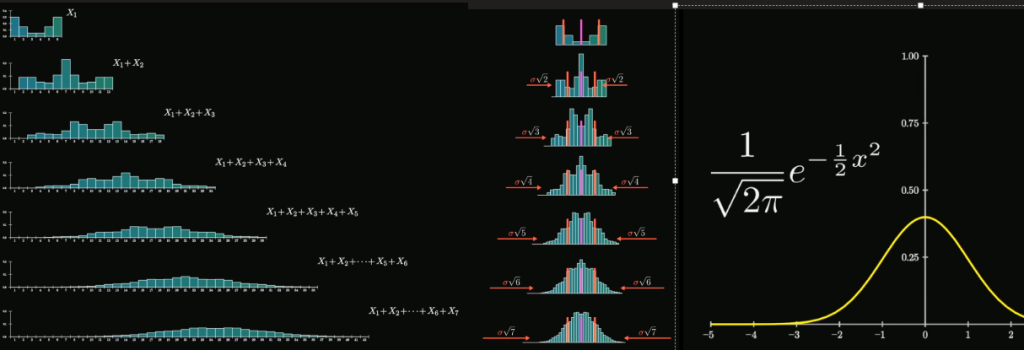
“随着随机变量的和的数量不断增加，样本和分布就会变得像正态分布(样本和的分布不断向均值方向移动，并且随着标准差的增大变宽)，无论原始数据是什么样的分布“

有时也会说为平均值的分布，因为平均值=S/n，相当于对”和”做了一次线性变换(除以常数n)。由于线性变换不改变分布的”正态性”，所以均值的分布也趋近于正态分布

在信息论中，熵（Entropy）表示一个系统的“混乱程度”或“不确定性”。
均匀分布的“混乱程度”是最大的，因为我们完全无法预测它会出现哪个值（每个都一样可能）。所以在给定取值范围时，均匀分布的熵是最大的。
但在两个限制下（能量守恒 + 方差固定），熵最大的概率分布就是正态分布。对于连续型随机变量，熵的定义为： $H(X)=-\int f(x)\ln f(x)dx$ 其中$f(x)$是概率密度函数。 当我们对分布施加均值固定（$E[X] = \mu$）和方差固定（$Var(X)=\sigma^2$）的约束时，通过数学推导（利用变分法或拉格朗日乘数法）可以证明： 只有正态分布的概率密度函数能使上述熵的表达式取得最大值。换句话说，如果我们只知道一个变量的平均值和方差，最“不确定”的分布就是正态分布

• 能量守恒(期望值约束)：限定了变量的均值（比如平均是0）
• 二次色散(方差约束)：限定了变量的方差，即波动范围不能随便乱来

例子：

“扔满足某概率分布的骰子很多次，每一次扔出N个骰子，N个骰子的和的分布满足正态分布”

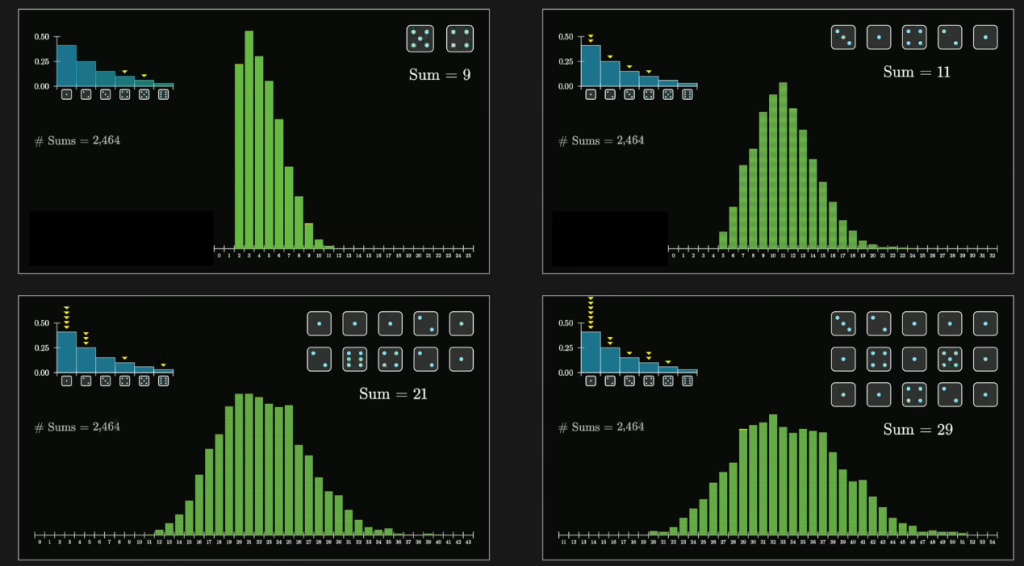
如果我们抛掷2/5/10/24个骰子并记录他们点数和的分布，随着我们抛出次数的增多，得到这个点数和的分布会越来越趋近钟形曲线。

只要满足独立同分布即可，因此对于任何点数分布的骰子都适用，该例中骰子就是非均质的

那你也许会问我们需要多少样本才能够代表

三个前提条件：

可视化理解(精心设计的分布函数)

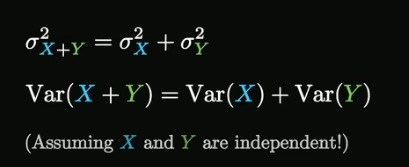
n个不同的独立随机变量的和的分布，和的分布的方差是这些分布方差的和，如果不独立则需要考虑协方差。对于和分布的平均值，无论变量是否独立，都为这些分布的平均值之和
n个同一独立随机变量的和的分布的

• 方差会是原始方差的n倍
• 标准差是分布方差根号下n倍
• 平均值为分布方差的n倍

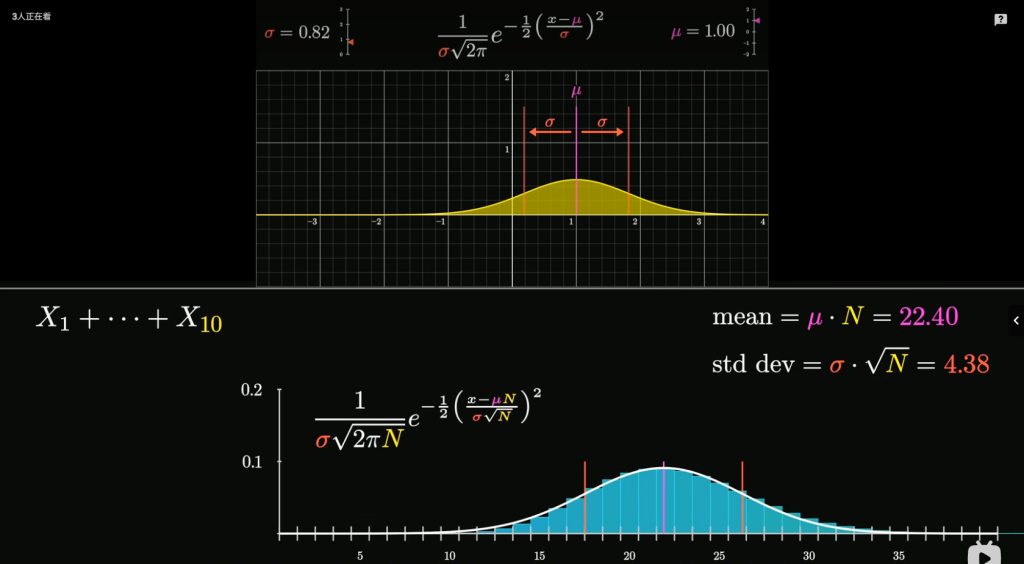
现在不再关注同一随机变量的和的分布，而是和 – N平均值 / 根号下N 标准差的分布，可知
这个分布的平均值为0，因此图像关于y轴对称, 标准差为1

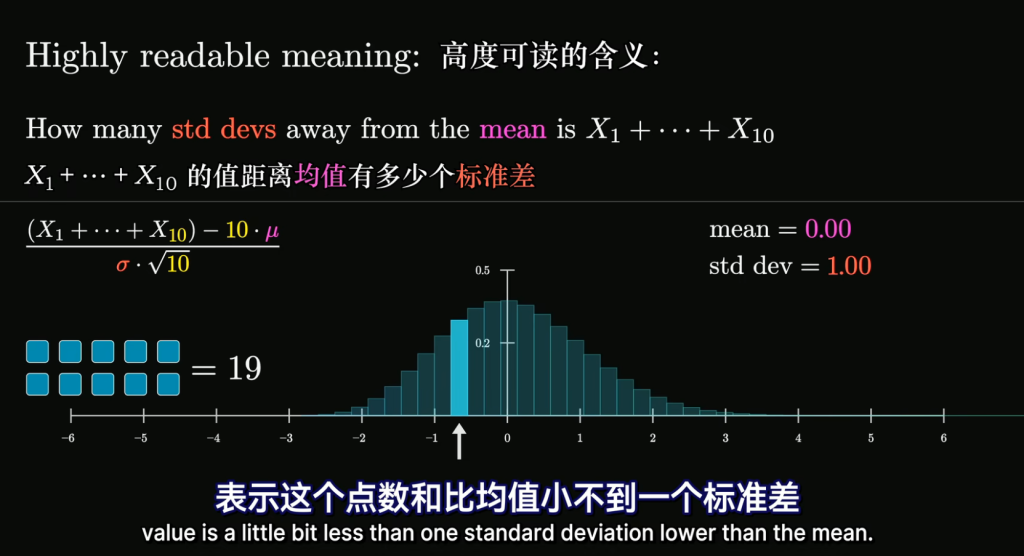
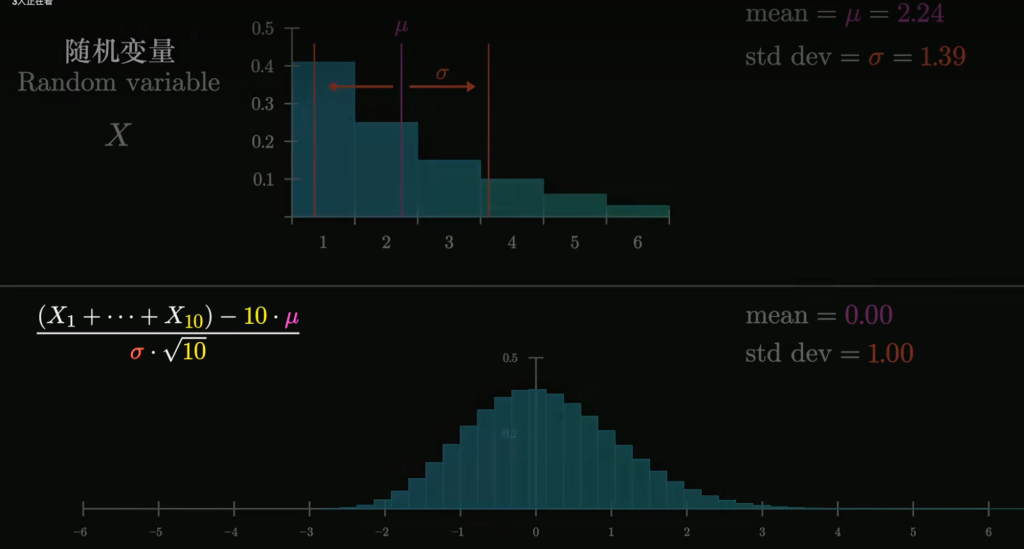
而这个修改后看起来变量和的分布从正态分布变为标准正态分布，而我们选取的变量的数量很多时，无论变量X的分布有多么极端，最终其改后和的分布也一定会是标准正态分布

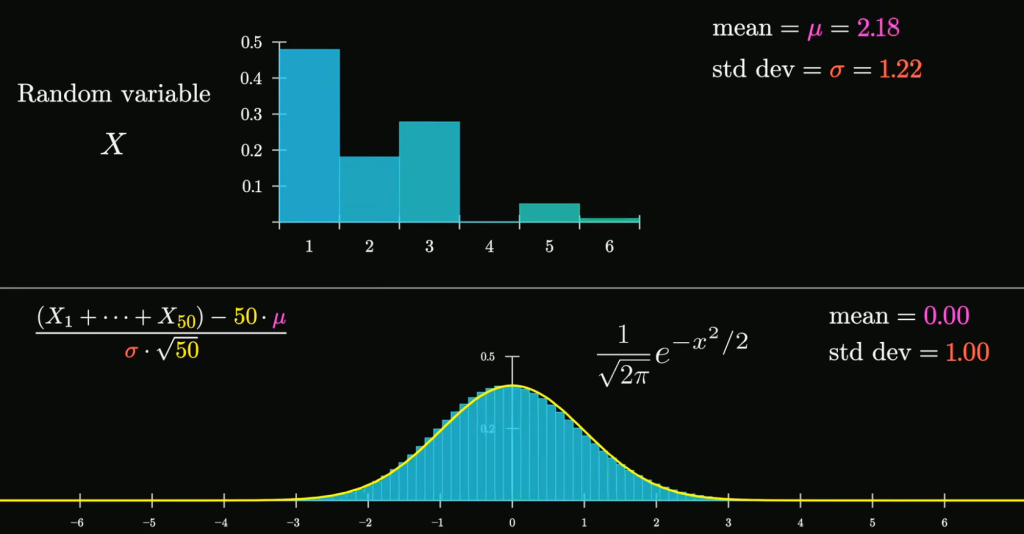
同样，无论这个随机变量的分布是什么，将多个相同的随机变量相加后，随着相加变量的数量增加，它们的分布形状逐渐接近正态分布

所有形象化理解的过程到此结束，下面我们给出数学上对中心极限定义的严格定义：

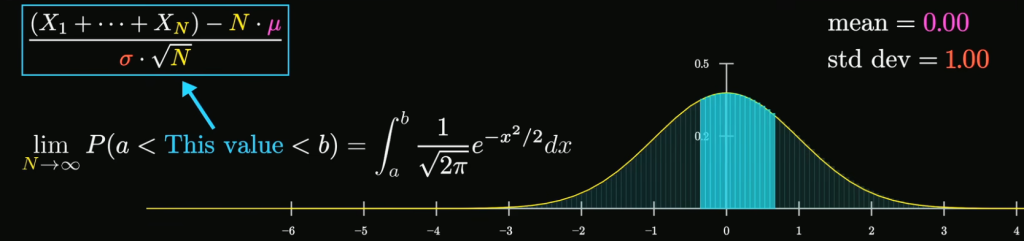
如果某个变量(构造的和)落在两个给定的实数a和b之间的概率，从他的极限角度看，当N趋于无穷大时，这个极限的值等于标准正态分布区间[a,b]的积分，即标准正态分布曲线在这两个值之间的面积

公式形象记忆

底数与指数：

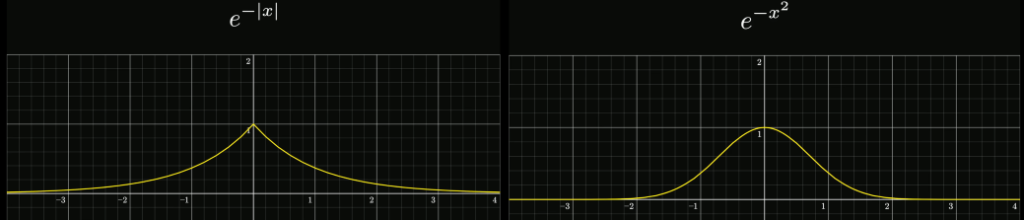
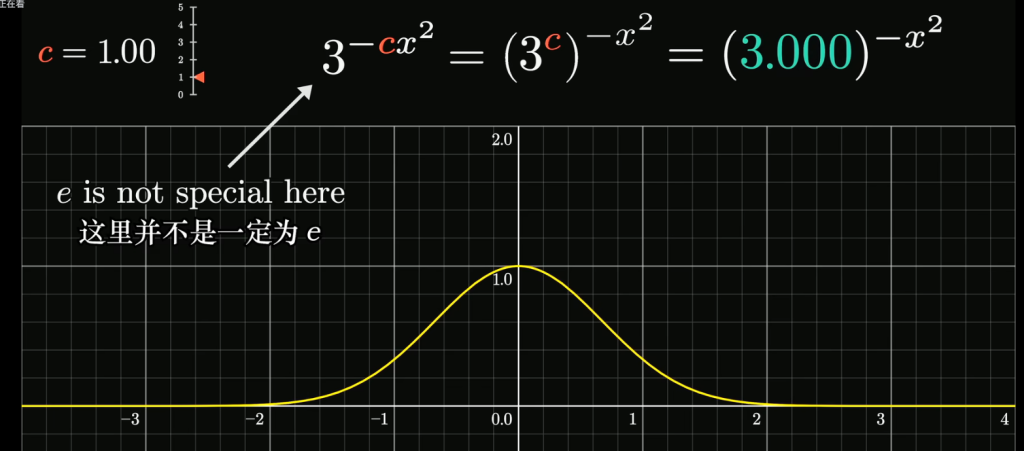
指数的变化等价于底数对应的变化，所以e作为指数的底数并不是强制的，可以设为其他数改变相应的指数即可，但要满足底数大于1，取e是方便积分

指数的1/2

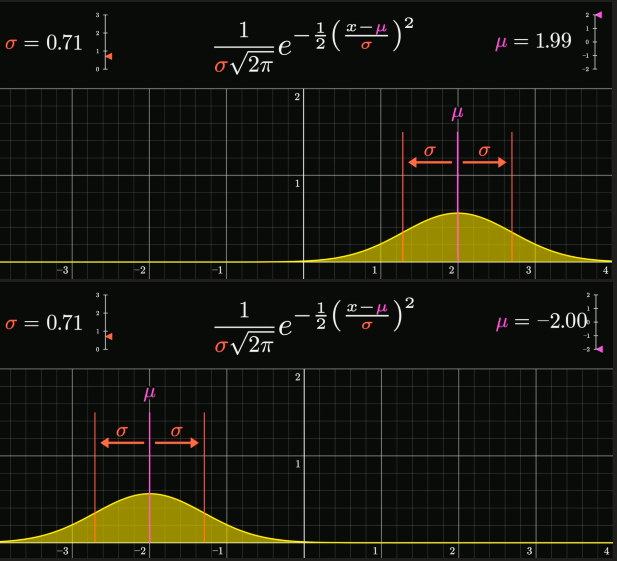
对于函数： \[ f(x) = e^{-\frac{1}{2}(\frac{x}{\sigma})^2} \] 当你对它求二阶导，会发现： – 在\(x = \pm\sigma\)时，二阶导数为\(0\) – 即图像的拐点（curvature changes）就在\(x = \pm\sigma\)处 – 所以，这个形式保证了：“一跳出1个标准差的距离，函数曲线的弯曲方向改变” ，恰好就是“钟形曲线”弯折的那个点

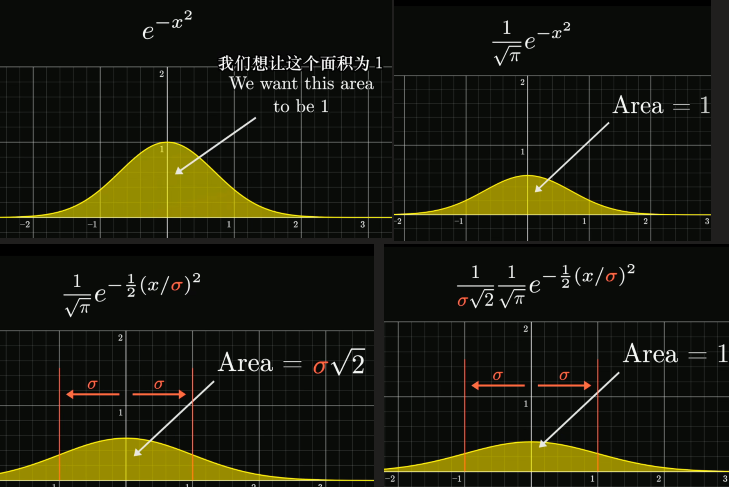
归一化系数

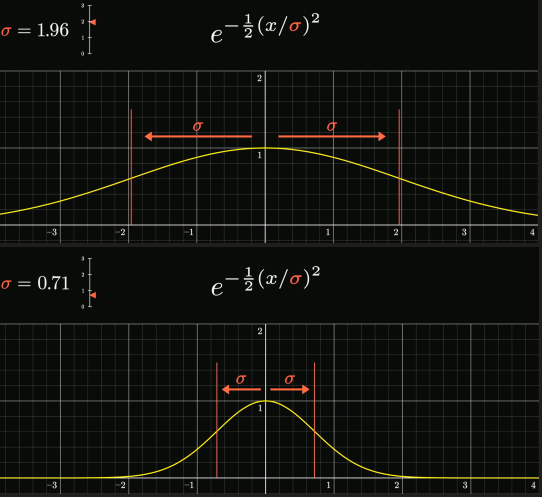
当改变σ时曲线会变窄变宽，为了让函数与X轴的面积为1(pdf图像的总面积代表总概率和)，在前面乘以归一化系数
当σ = 1时我们称之为标准正态分布(standard normal distribution)

此外X再减去一个参数 μ，调整μ可以左右滑动图像 描述了这个分布的均值