有约束条件的极值问题 – 条件极值

约束条件一定是等式

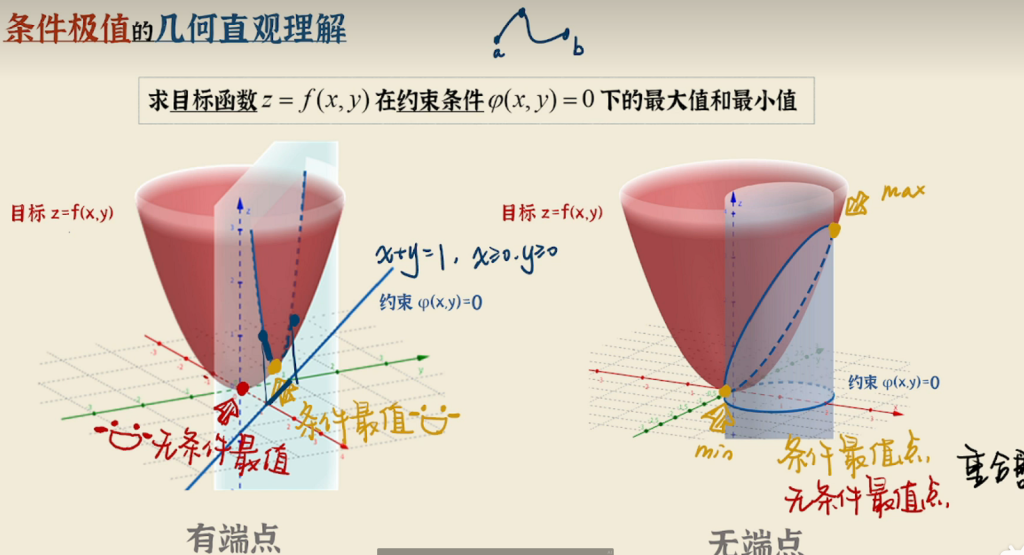
带约束极值问题是一类当想要在一个限制条件下，让某个函数 f(x,y)取得最大值或最小值（也叫极值），就要用拉格朗日数乘法

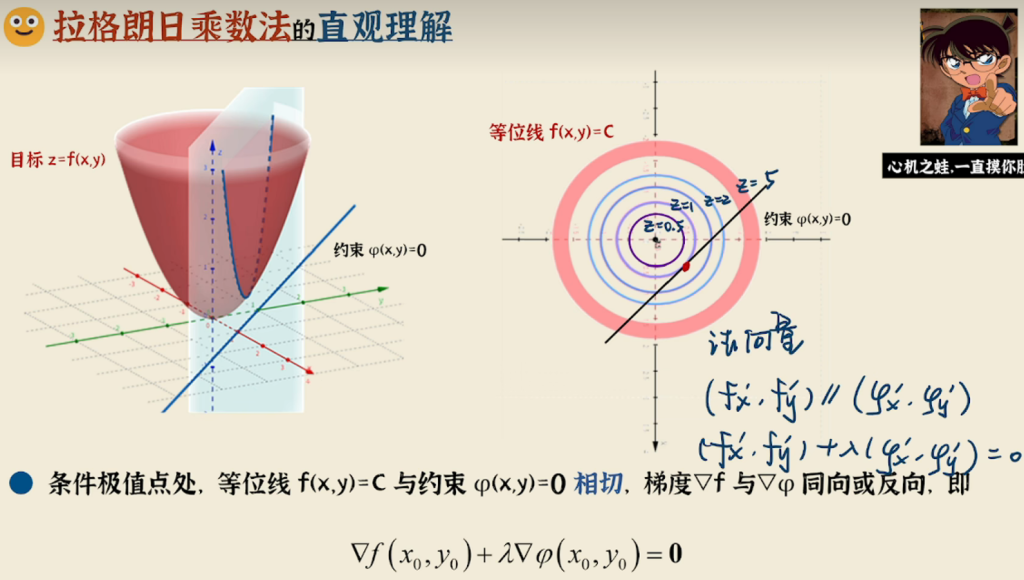
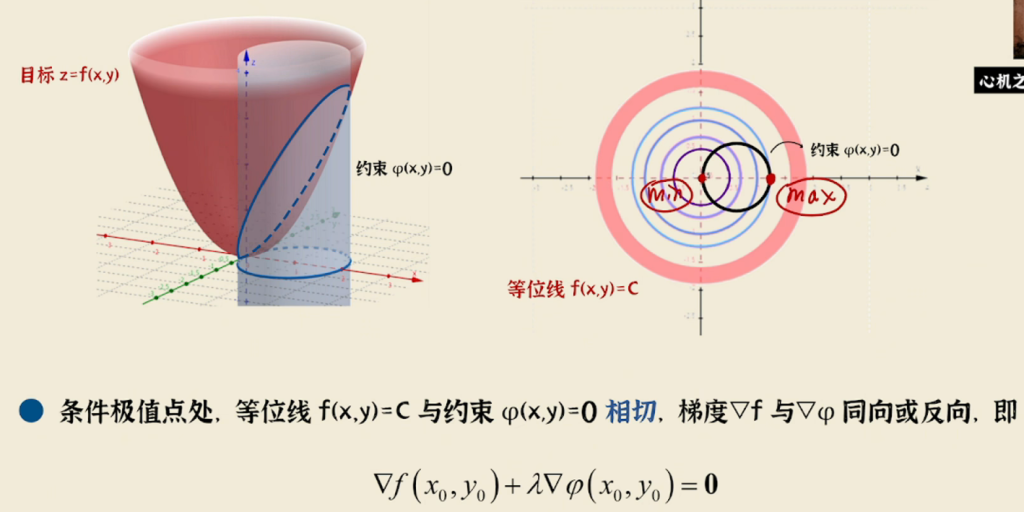
用拉格朗日法得到的驻点不一定是极值点

允许对目标函数做适当变形，本质是只要不影响驻点就可以

无论是几个限制条件解法都是由没有拉格朗日参数的前几个偏导之间，进行消参。再代入到对拉格朗日参数求导的式子里得到XYZ之间的关系

Example 1 At what point or points on the circle \(x^{2}+y^{2}=1\) does \(f(x, y)=x y\) have an absolute maximum, and what is that maximum?

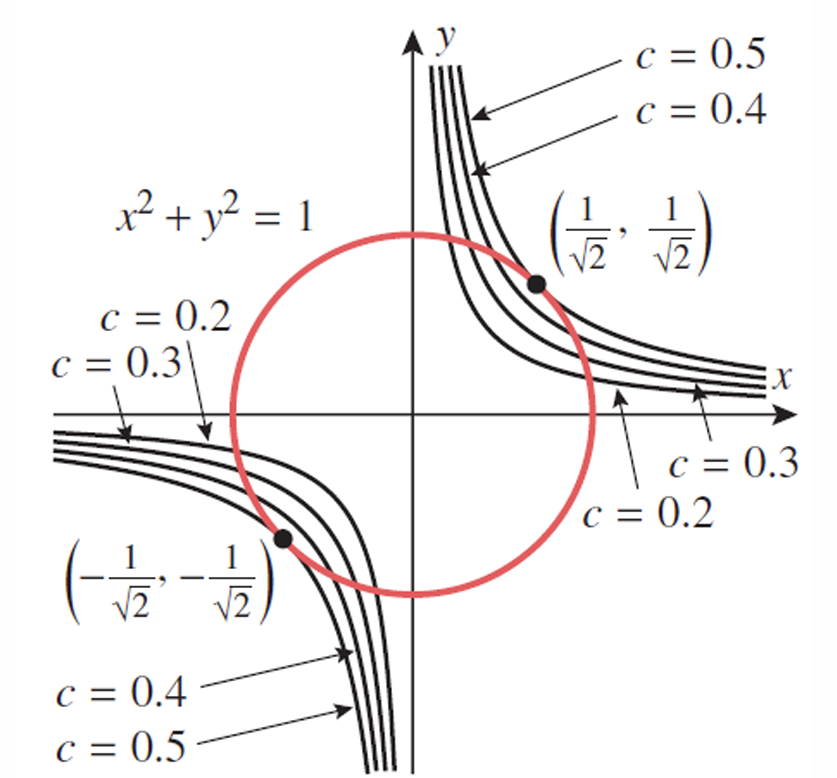
因此，函数\(f(x,y)=xy\)的绝对最大值为\(\frac{1}{2}\)，出现在两个点\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)和\((-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)处。虽然题目没有要求，但我们也可以看到f的绝对最小值为\(-\frac{1}{2}\)，出现在点\((\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)和\((-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)处。图 13.9.3 展示了一些等值线\(xy=c\)和最大值附近的约束曲线。对于最小值，可以使用c为负值的等值线\(xy=c\)来获得类似的图形。

例2：

例3：