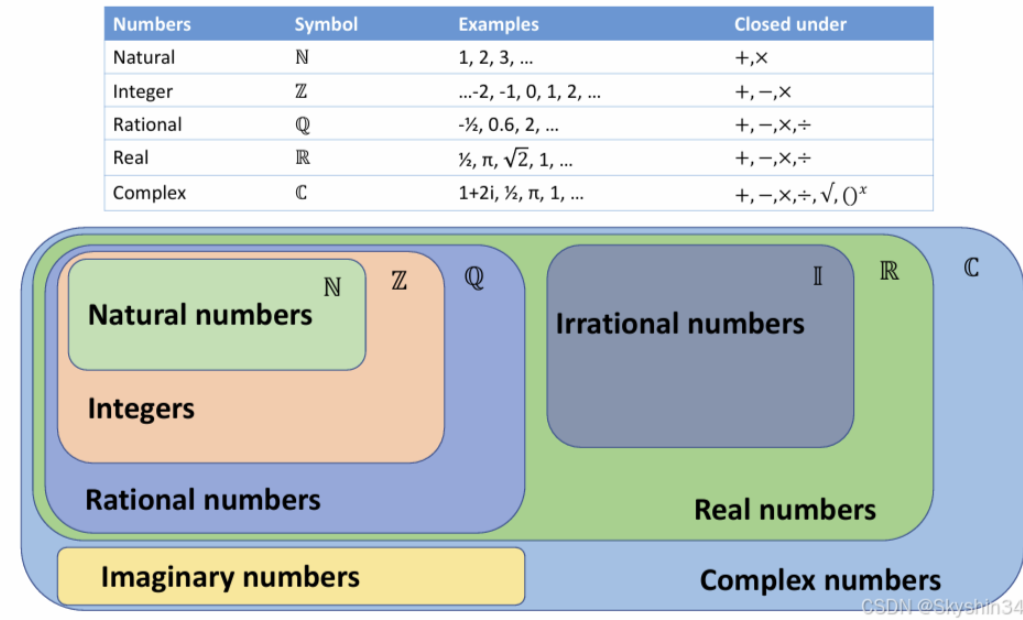
封闭性

如果对一个集合的成员进行运算 的成员总是产生该集合的成员，那么这个集合就是封闭的(Set is closed)

自然数(不包括0)在加法运算下是封闭的，但在减法运算下不是。 我们需要扩展自然数集，把 0 和负数包括进来才能使自然数集在减法运算下封闭。

整数是集合 Z = {…,-4,-3,-2,-1,0,1,2,3,4,…}。
整数在加法和减法运算下是封闭的。如果我们引入除法运算，就需要扩展我们的数系，将分数也包括在内。

有理数在加法、减法、乘法、除法中都是封闭的。 但幂和根不封闭。Real numbers are closed under addition, subtraction, multiplication and division, but not under power and roots.

在 R 中，方程 \(x^2\) = -1 没有解。因此，我们发明了一个新的数，称为虚数imaginary numbers i。

 实数加上虚数，就是最广泛的一类数： 复数。

Norm/absolutevalue 模长

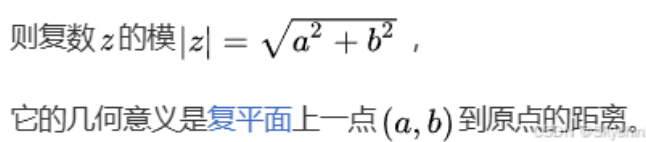
Complex conjugation 共轭复数

辐角 Argument of a complex number & 辐角主值 principle value of the argument

注意其范围和表示。一定要画图，因为tanx的周期是Π，计算的辐角值+Π也能得到相同的tanb/a，所以要看图决定是否加Π（周期）

3种表达方式

表示复数的方法有：

• 定义中的实数+虚数
• 复平面(又称Argand diagram阿甘图)中通过向量的坐标表示
• 复平面中结合极坐标用三角函数表示

笛卡尔和极坐标表示的转化

从polr到Cartesian将三角函数的值算出即可

从Cartesian到polar

如果用tan的方式计算从笛卡尔到极坐标的角度转换，先画图判断笛卡尔表示下复数在第几象限，因为tan的周期是Π，对于角度不同的角，结果是一样的，要根据实际角度，加减Π调整结果

如果X/Y =0，画图就可知道角度，不用再计算了

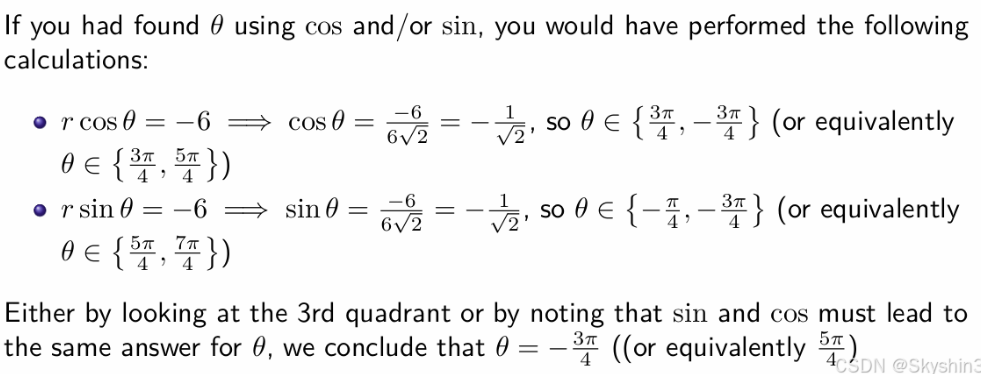
运算

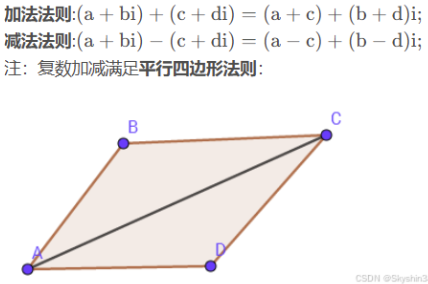
加减法

 除法

笛卡尔表示：把除法换算成乘法做，在分子分母同时乘上分母的共轭。互为共轭的两个复数相乘是个实常数。这样做主要是在进行除法运算时，使分母变成一个实数，方便计算。

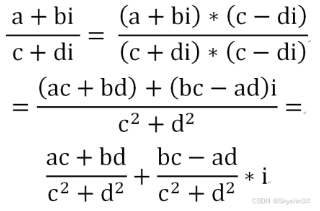
极坐标表示

乘法

De Moivre 公式（棣莫弗定理）

复数根

eg1：计算含幂复数的根(root):De moivre

• 注意r大于0
• 复数转化为极坐标表示时注意tanx通过画图判断是否要加0
• 如果用Demovir通常是有幂，多少幂就有多少个根或者解，所以要在转化的那一步没进行任何操作时，给角度加2kΠ

 eg2 求解复数方程：De moivre

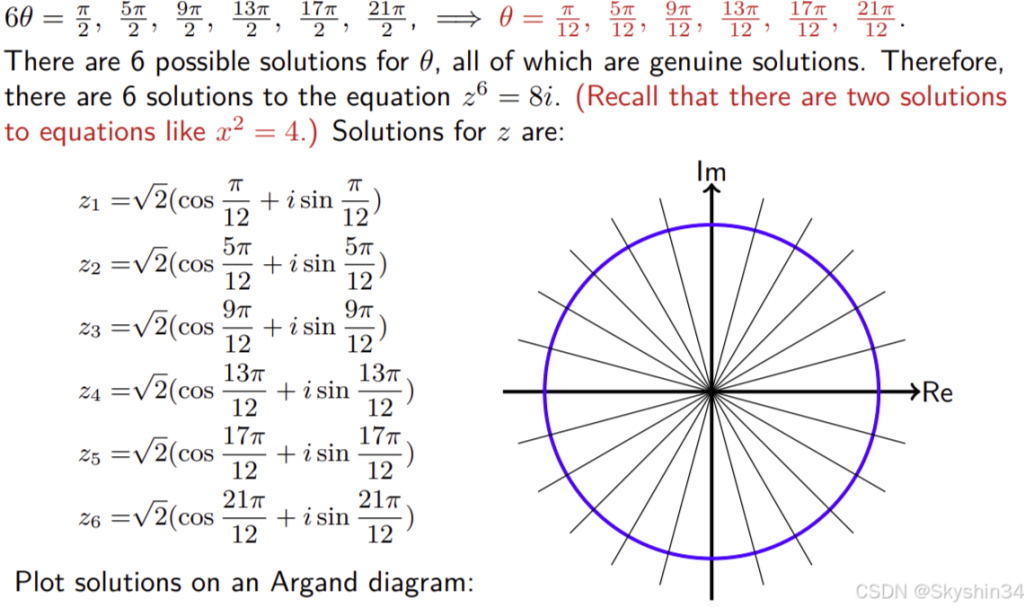
eg4.通解公式quadratic formula + 设欧拉解/ 凑平方complete the square求复数多于一项的复数方程的根

eg5.根据复数根的共轭性将一个根拓展到两个根，从而找到该方程的其他根Roots of Polynomials