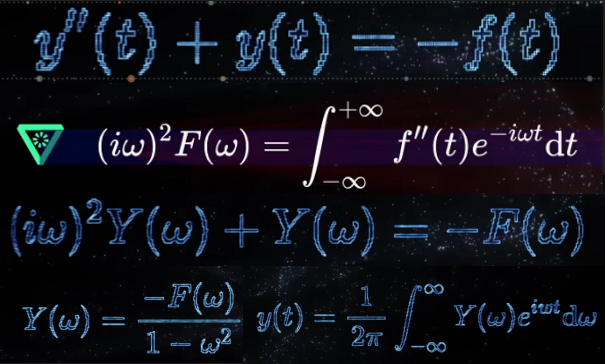卷积的“卷”，指翻转，从 X变成 -X的过程
“卷”还有滑动的含义-k -> n-k 是平移

卷积的“积”，指的是积分（连续）/加权求和（离散）。

因此卷积的运算过程是翻转->平移->求和

所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加得到一个新的序列(a∗b)n​：n表示卷积结果序列中元素的位置索引。比如(a∗b)0​指的是卷积结果序列中第 0 个位置的元素，(a∗b)1​指第 1 个位置的元素，以此类推。卷积是一种组合数组或函数（而不是数字）的方法

线性卷积

参与运算的是两个有限长度的非周期序列。对长度为 N 的序列 x (n)，与长度为 M 的序列 h (n) 进行卷积。其卷积结果的序列 y (n)长度为L = M+N-1

连续时间线性卷积：对于连续时间信号 \(x(t)\)（输入信号）和 \(h(t)\)（系统冲激响应）：$$y(t) = (x * h)(t) = \int_{-\infty}^{\infty} x(\tau) \cdot h(t – \tau) \, d\tau$$

对于离散序列 \(x[n]\)（长度 N ）和 \(h[n]\)（长度 M ），线性卷积公式为：$$y[n] = (x * h)[n] = \sum_{k = -\infty}^{\infty} x[k] \cdot h[n – k]$$

• 上下限的差为卷积的长度即可，此外还要修改滑动序列的自变量，具体见下例

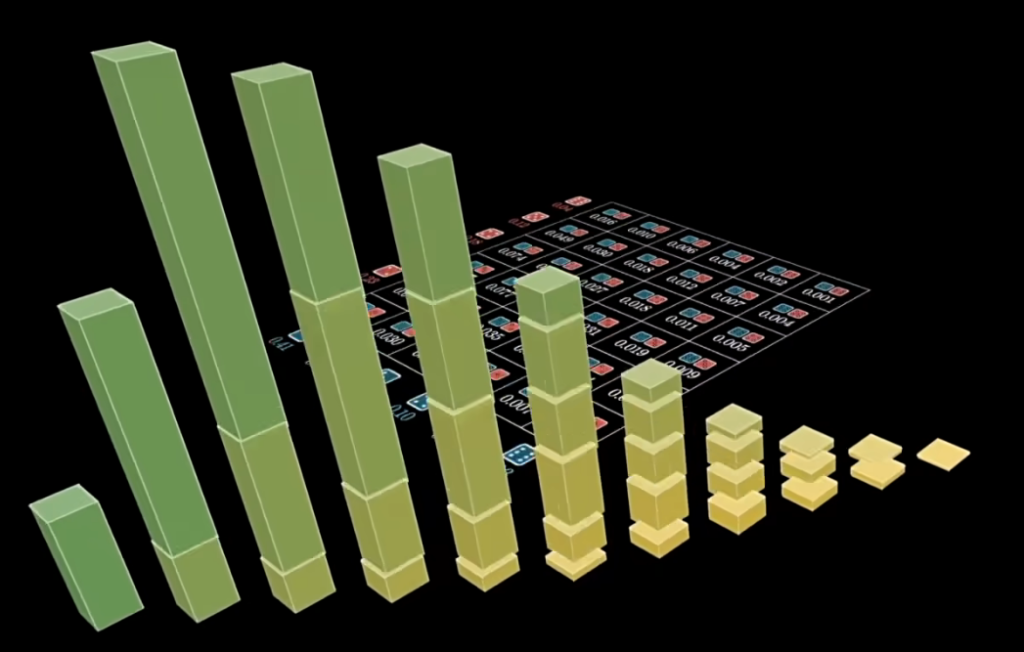
离散随机变量的卷积 – 抛筛子案例

前提条件：两个随机变量相互独立

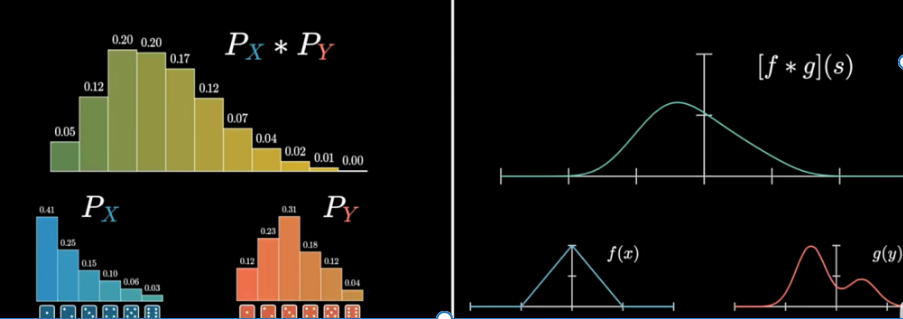
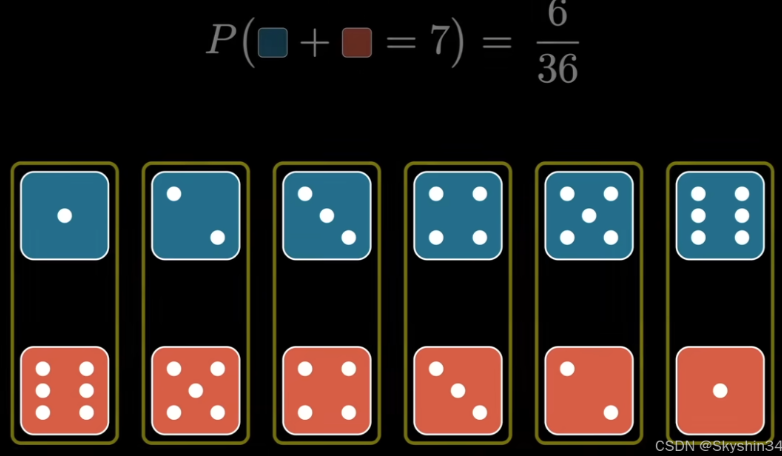
设定两个不同非均质骰子，计算投掷两个骰子可能的点数和，和对应的发生概率，我们可以列出所有点数组合以及发生的概率：

同一对角线上的点数组合的点数和相同，将同一对角线的点数组合的概率相加即可得到点数和的概率

看起来求点数和概率的过程就是沿着对角线求概率可视化的高度的和
虽然看起来有点画蛇添足，但类比连续随机变量时，可以直观的建立“卷积是在求对角切片”的直觉

思考另一种方式展示这个问题：把其中一个分布水平翻转，这样所有点数和相同的组合就会纵向对齐，通过平移翻转的分布，可以得到不同的点数和。此时求点数和的概率，可通过求对齐的点数组合的概率相乘再全部相加

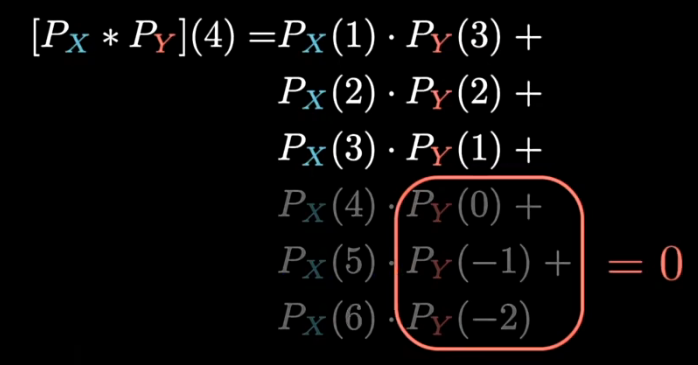
离散概率分布函数为了保证总和为1，x=1~6以外取值都是0

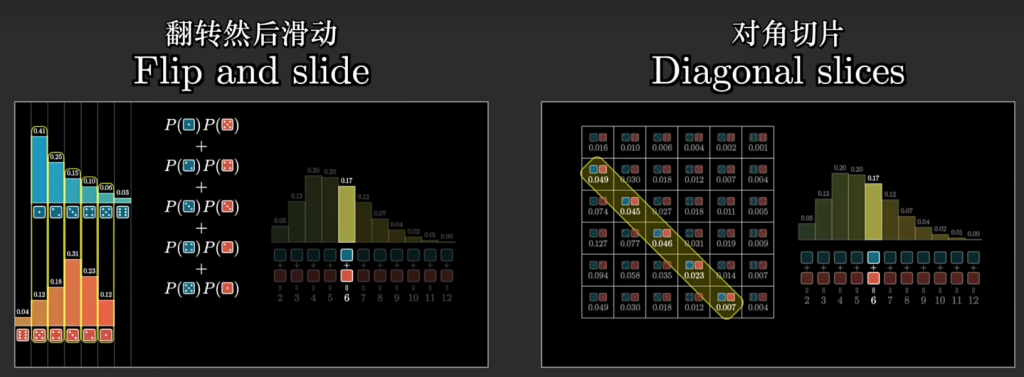
两种不同的可视化方式都在描述同一个基本操作：输入两个不同的独立分布，输出一个描述和的概率分布
两个离散独立随机变量X和Y，他们的和X+Y的概率分布可以这样计算：

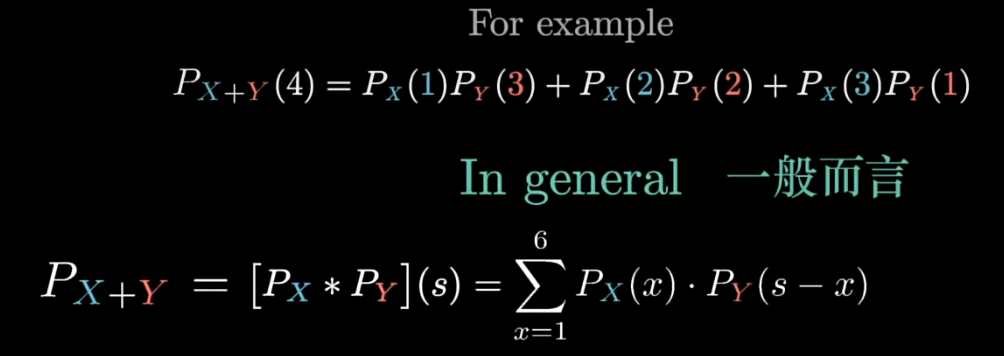
连续随机变量的卷积

同样进行翻转和平移，第三步从原来的对PMF的乘积进行求和，变成对PDF的乘积进行积分

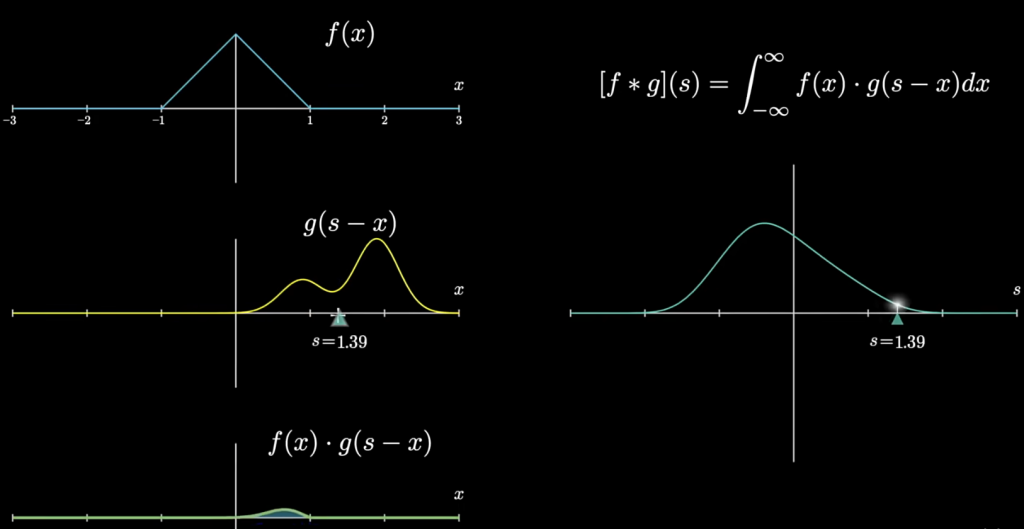
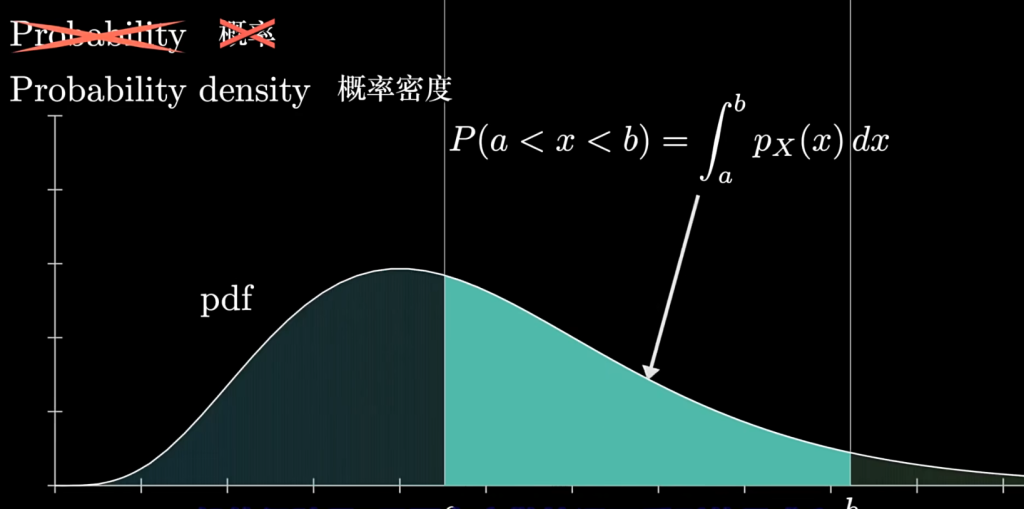
对于离散变量的概率通过概率分布函数的值即高度计算，但计算连续变量的概率需要通过计算概率密度函数的定积分，高度本身没有意义

卷积的直观几何解释：离散变量相加时，我们用表格+对角线来加概率；连续变量相加的本质也是一样，只不过从“加格子的高度”变成了“求面积”，从“求和”变成了“积分”。

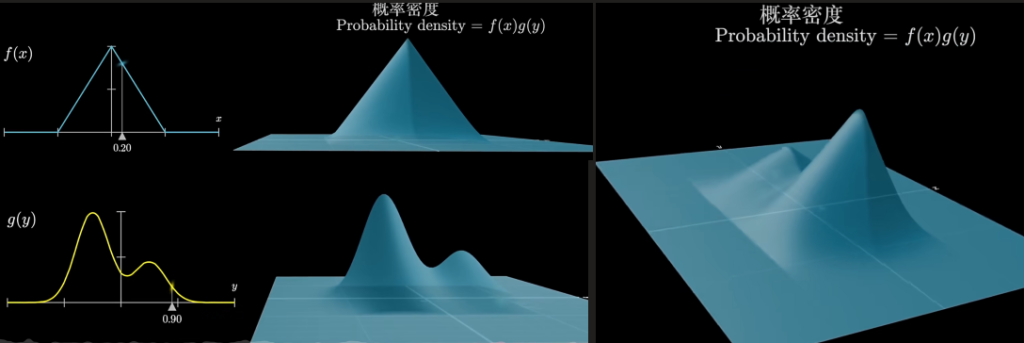
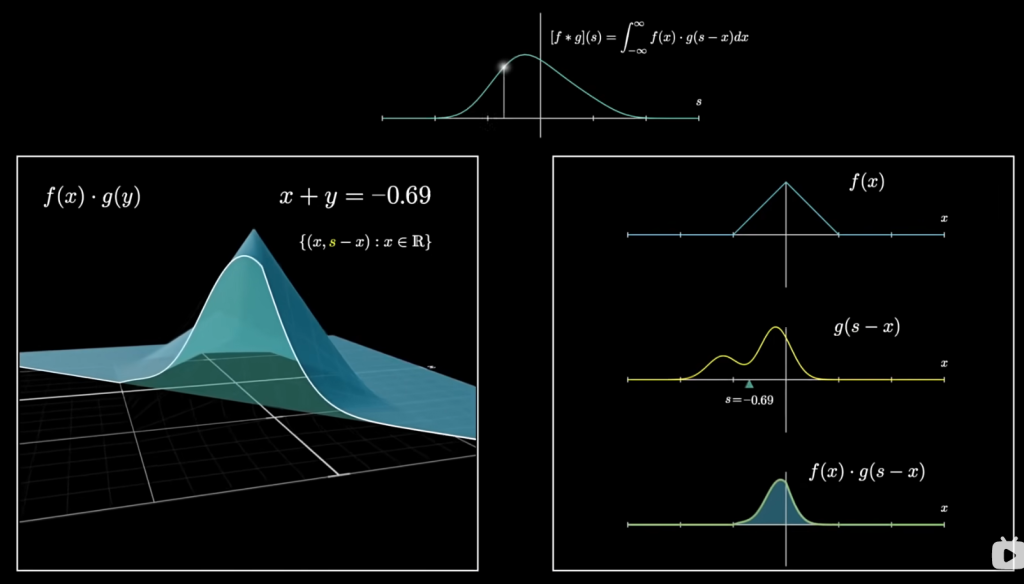
两个卷积中输入量之和为固定值时概率密度函数的乘积与概率密度函数的对角线的图形是相同的

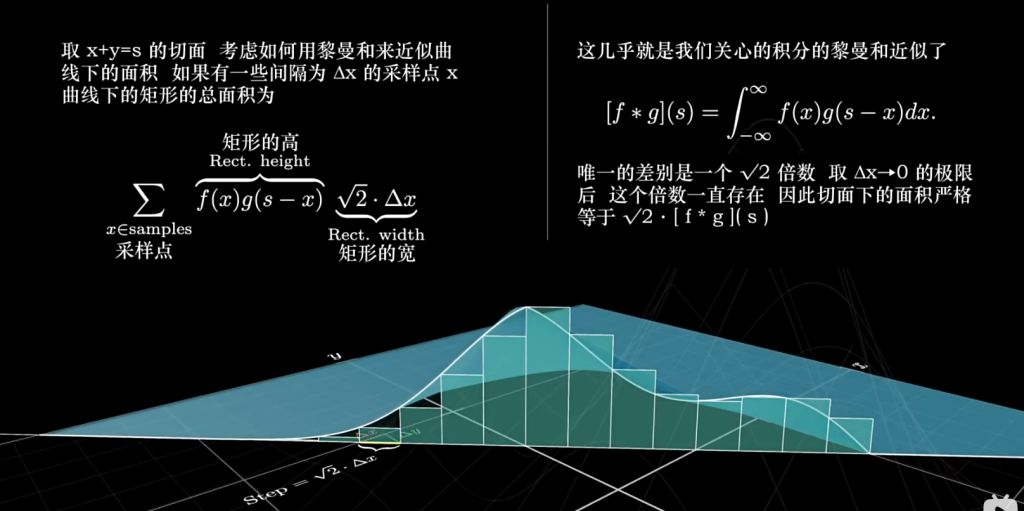
实际得到卷积结果时，截面需要除根2

卷积与中心极限定理的联系

卷积的意义：对于两个独立随机变量 X 和 Y，它们的和 \(Z = X + Y\) 的概率分布，是 X 和 Y 分布的卷积。 推广到 n 个独立同分布的随机变量，它们的和 \(S_n = X_1 + X_2 + \dots + X_n\) 的分布，就是这 n 个变量分布的 “n 重卷积”（反复叠加卷积的结果）

中心极限定理的卷积视角
中心极限定理说的是：当 n 足够大时，无论单个变量 \(X_i\) 的分布是什么（只要满足一定条件，比如方差有限），它们的和 \(S_n\) 的分布（即 n 重卷积的结果）会越来越接近正态分布。
简单说：独立变量和的分布=分布的卷积，大量卷积叠加→趋近正态分布

验证独立变量
两个独立的均匀分布随机变量求和 假设：
随机变量 \( X \) 的取值为1、2，概率均为0.5（分布记为 \( P_X(x) \) ）
随机变量 \( Y \) 的取值为1、2，概率均为0.5（分布记为 \( P_Y(y) \) ）
\( X \) 与 \( Y \) 独立，求它们的和 \( Z = X + Y \) 的分布。
列出各自的分布 – \( P_X(1) = 0.5 \)，\( P_X(2) = 0.5 \)（其他值概率为0）； – \( P_Y(1) = 0.5 \)，\( P_Y(2) = 0.5 \)（其他值概率为0）。
计算 \( Z = X + Y \) 的可能取值及概率 \( Z \) 的可能值为2（1+1）、3（1+2或2+1）、4（2+2）： – \( P(Z = 2) = P(X = 1 \) 且 \( Y = 1) = P_X(1) \cdot P_Y(1) = 0.5 \times 0.5 = 0.25 \)； – \( P(Z = 3) = P(X = 1, Y = 2) + P(X = 2, Y = 1) = 0.5 \times 0.5 + 0.5 \times 0.5 = 0.5 \)； – \( P(Z = 4) = P(X = 2, Y = 2) = 0.5 \times 0.5 = 0.25 \)。
对比“卷积”的计算 离散情况下，两个分布的卷积公式为： \[ P_Z(z) = \sum_{x} P_X(x) \cdot P_Y(z – x) \] 代入计算： – 当 \( z = 2 \)：\( P_X(1) \cdot P_Y(1) + P_X(2) \cdot P_Y(0) (P_Y(0) = 0) \) → 结果0.25； – 当 \( z = 3 \)：\( P_X(1) \cdot P_Y(2) + P_X(2) \cdot P_Y(1) \) → \( 0.5×0.5 + 0.5×0.5 = 0.5 \)； – 当 \( z = 4 \)：\( P_X(1) \cdot P_Y(3)(0) + P_X(2) \cdot P_Y(2) \) → 0.25。 结果完全一致：\( Z \) 的分布就是 \( X \) 和 \( Y \) 分布的卷积。

循环(圆周、圆)卷积 cyclic / circular convolution

参与运算的是两个有限长度的非周期序列，所得结果有限序列的长度仍为N:

设两个有限长序列 \(x[n]\)（长度 \(N_x\)）和 \(h[n]\)（长度 \(N_h\)），补零至长度 N 后，圆周卷积定义为：$$y_{\text{circ}}[n] = \sum_{k=0}^{N-1} x[k] \cdot h\left[(n – k) \mod N\right], \quad n = 0, 1, \dots, N-1$$

例题：

周期卷积 Periodic Convolution

周期卷积的输出是一个长度为周期 P 的有限序列，但它是一个周期序列在一个周期内的值，本质上代表一个无限周期信号的一个周期片段。

设两个有限长度序列 \(x[n]\)（长度 \(N_x\) ）和 \(h[n]\)（长度 \(N_h\) ），将它们按周期 P 进行周期延拓，得到无限周期序列 \(\tilde{x}[n]\) 和 \(\tilde{h}[n]\)，则它们的周期卷积定义为：

将有限长序列 \(x[n]\) 和 \(h[n]\) 以周期 N 延拓为无限长周期序列 \(\tilde{x}[n]\) 和 \(\tilde{h}[n]\)，则它们的 周期卷积 为：$$y_p(n) = \sum_{k=0}^{P – 1} x(k) \cdot h((n – k) \bmod P)$$

• 由于周期性，上式在一个周期内（\(k = 0\) 到 \(N-1\)）的求和结果与圆周卷积完全一致，即：\(y_{\text{circ}}[n] = \tilde{y}[n] \cdot R_N[n]\) 其中 \(R_N[n]\) 是长度为 N 的矩形窗函数（仅在 \(n = 0, 1, \dots, N-1\) 时为 1，其余为 0）。

结论：圆周卷积是周期卷积在主值区间（一个周期内）的结果，二者本质相同，“圆周” 和 “循环” 均描述其周期性循环的特性。

其实就计算结果来讲周期卷积和循环卷积没有什么区别，这也是为什么很多文章不做区分且经常混淆的原因

• 线性卷积：一次性铺平滑动相乘（不折叠）
• 圆周卷积：边界会“绕一圈”回来累加
• 周期卷积：把信号视为无限重复的周期版本做圆周卷积

怎样将两个不同长度所进行的线性卷积转化为循环卷积

循环卷积要求两个序列的长度相等，因此在两个序列后添加0使其变为与输出序列等长的周期序列。一切循环卷积都可以通过傅里叶变换计算，线性卷积需要经过上述转化后使用傅里叶变换计算(暂时没搞懂)

用傅里叶变换计算卷积的原因：快速傅里叶变换，降低复杂度

线性卷积矩阵表示：

卷积计算过程中相乘又相加的计算属性可以让我们用矩阵表示。

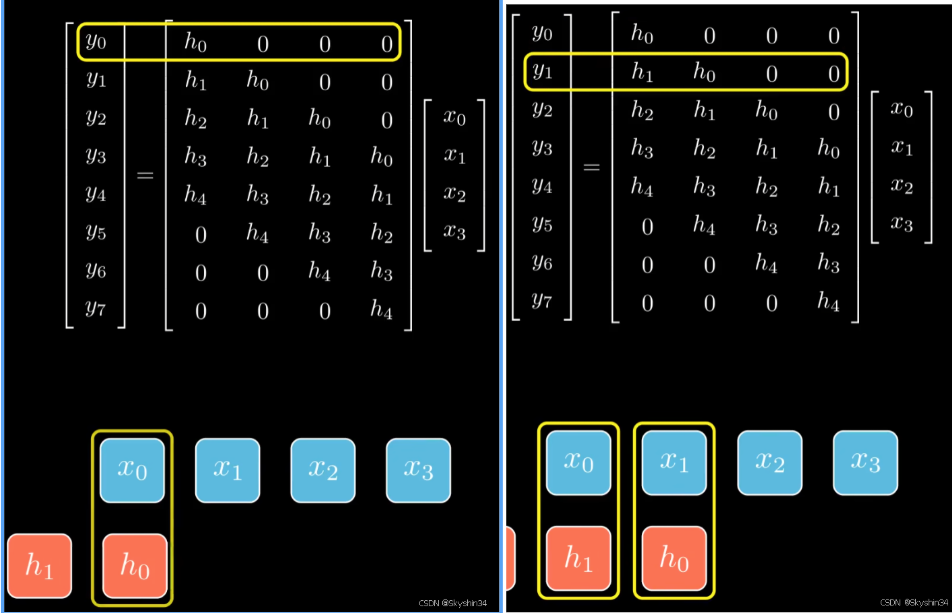
反转序列的右移用矩阵的行来体现，每行代表此时与X对齐的元素，未对齐的元素用0表示

性质

数组之间的加法和乘法一样，对数组的卷积也具有以下三个基本性质

交换律：f * g = g * f

结合律：(f * g) * h = f * (g * h) 多重卷积的计算顺序可以随意改变。

分配律：f * (g + h) = (f * g) + (f * h)

平移性：\(f(t – t_0) * g(t) = (f * g)(t – t_0)\)

卷积定理

FT & DFT 傅里叶变换 – Skyshin34的博客参见傅里叶变换性质 – 调频性质部分

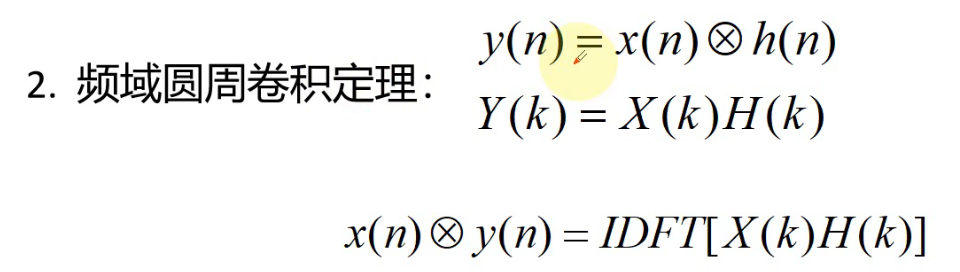
香农采样定理

是连续信号（通常称作“模拟信号”）与离散信号（通常称作“数字信号”）之间的桥梁，为模拟信号转换为数字信号提供了一个数学准则。它确定了信号带宽的上限，或能捕获连续信号的所有信息的离散采样信号所允许的采样频率的下限。

定理表述：

如果一个信号的带宽是有限的，即信号中不包含任何高于某一最大频率 \( f_{\text{max}} \) 的频率分量，那么我们可以用一个大于或等于该信号最高频率的两倍的采样率 \( f_s \geq 2f_{\text{max}} \) 对该信号进行采样，以便在不丢失信息的情况下重建该信号。

采样率 \(( f_s )\)：每秒钟从信号中采集样本的数量，单位为赫兹 (Hz)。
带宽 \(( f_{\text{max}} )\)：包含谐波的最高频率与最低频率之差，即该信号所拥有的频率范围

应用

滑动均值滤波，模糊

每次迭代相当于将数据中的每个元素都乘以1/5，然后将它们加起来 – 求这个小窗口数据的平均值，总的来说，这个过程给了你一个原数据的平滑版本（滑动均值滤波）

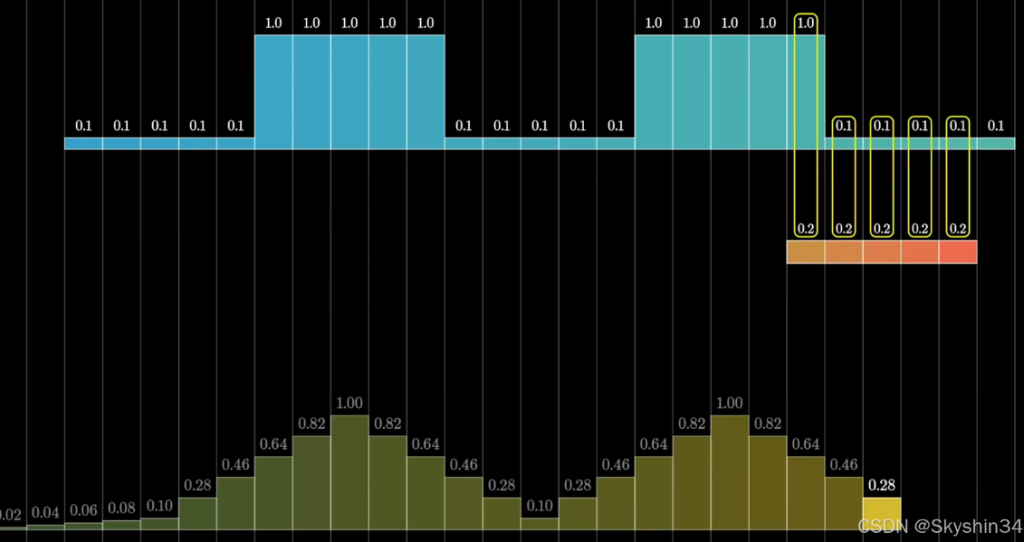
如果你在二维上进行类似的操作，就能得到一个把图片变模糊的方法卧槽这不是抗锯齿的算法的模糊化。用一个3×3的网格沿着原图像移动

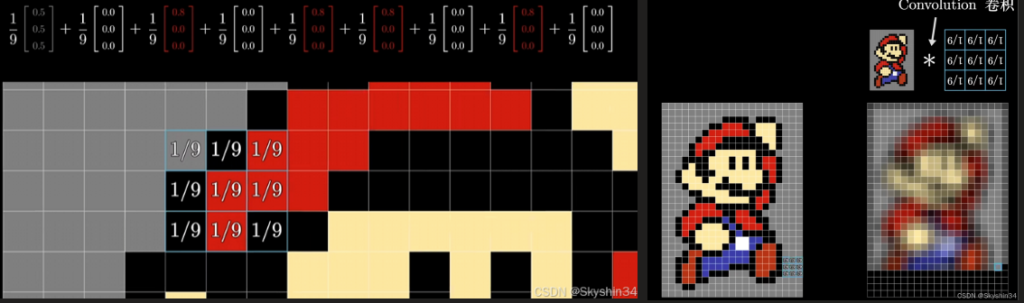
我们把颜色当作三维向量。将每个向量都乘以1/9然后求和就得到每个颜色通道的平均值，就得到每个颜色通道的平均值。对每个像素都如此计算，相当于每个像素都混杂了一部分到相邻的像素，这就得到了一个比原图更模糊的版本，用术语来说：右图就是原图和旋转180°小网络的卷积（本例中是否旋转无区别）