人工智能的发展过程

人工智能

一些人工智能项目力求将关于世界的知识用形式化的语言进行硬编码 (hard-code)
计算机可以使用逻辑推理规则来自动地理解这些形式化语言中的申明，这就是众所周知的人工智
能的知识库 (knowledge base) 方法；这些项目没有获得重大的成功

机器学习

简单的机器学习算法的性能在很大程度上依赖于给定数据的表示 （representation）

在整个计算机科学乃至日常生活中，对表示的依赖都是一个普遍现象，表示的选择会对机器学习算法
的性能产生巨大的影响

• 在计算机科学中，如果数据集合被精巧地结构化并被智能地索引，那么诸如搜索之类的操作的处理速度就可以成指数级地加快
• 人们可以很容易地在阿拉伯数字的表示下进行算术运算，但在罗马数字的表示下运算会比较耗时

现状：许多人工智能任务的解决方式——先提取一个合适的特征集，然后将这些特征提供给简单的机器学习算法

问题：对于许多任务来说，很难知道应该提取哪些特征

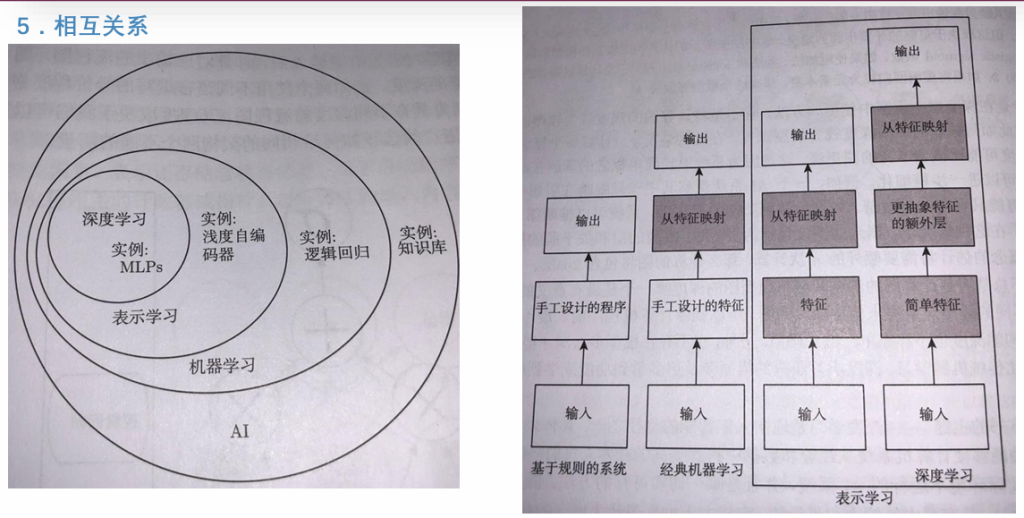
表示学习

表示学习：使用机器学习来发掘表示本身，而不仅仅把表示映射到输出。这种方法我们称之为表示学习。传统机器学习中，我们通常手动设计数据的表示（特征），然后让模型学习如何将这些表示映射到输出。而表示学习的方法是让模型直接从数据中自动学习有用的表示，而不仅仅是学习从固定表示到输出的映射。这种自动学习表示的方法称为表示学习

表示学习算法学习到的表示往往比手动设计的表示表现得更好，并且它们只需最少的人工干预，就能
让AI系统迅速适应新的任务

• 现状：当设计特征或设计用于学习特征的算法时，目标通常是分离出能解释观察数据的差异因素(factors of variation)
  • 当分析语音记录时，差异因素包括说话者的年龄、性别、他们的口音和他们正在说的词语
  • 当分析汽车的图像时，差异因素包括汽车的位置、它的颜色、太阳的角度和亮度

• 问题1：很多差异因素影响着能够观察到的每一个数据—数据受多重差异因素影响（多变性）
  • 在一张包含红色汽车的图片中，其单个像素在夜间可能会非常接近黑色
  • 汽车轮廓的形状取决于视角
• 问题2：从原始数据中提取高层次、抽象的特征是非常困难的
  • 许多诸如说话口音这样的变差因素，只能通过对数据进行复杂的、接近人类水平的理解来辨识

深度学习

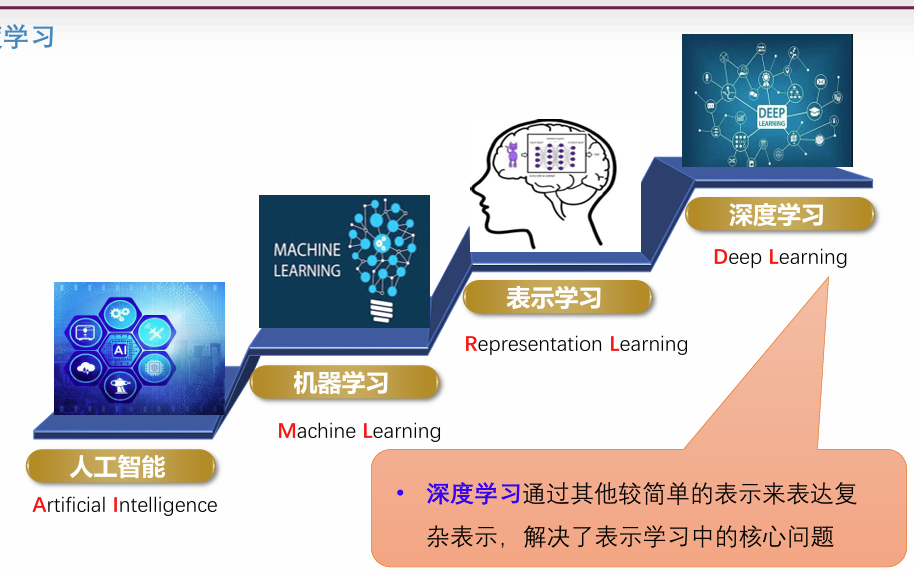
深度学习让计算机通过较简单概念构建复杂的概念，典型例子是前馈深度网络或多层感知机
多层感知机仅仅是一个将一组输入值映射到输出值的数学函数，由许多较简单的函数复合而成。可以认为不同数学函数的每一次应用都为输入提供了新的表示

神经网络

人工神经网络（Artificial Neural Network, ANN），由大量处理单元互联组成的非线性、自适应信息处理系统

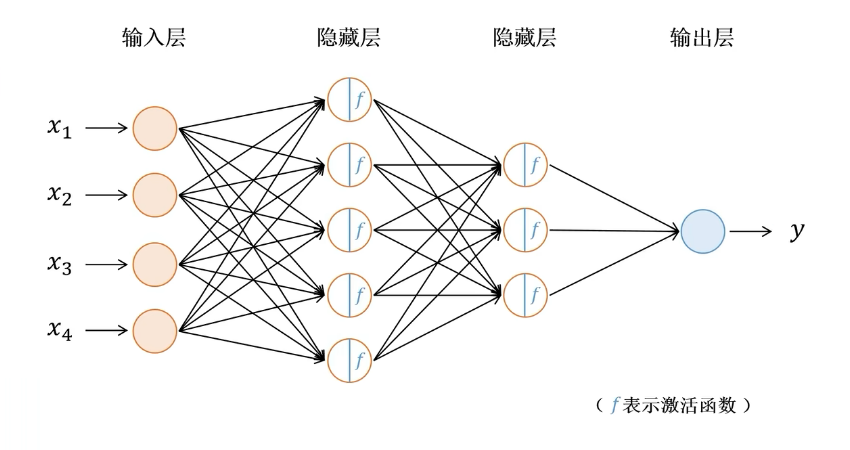
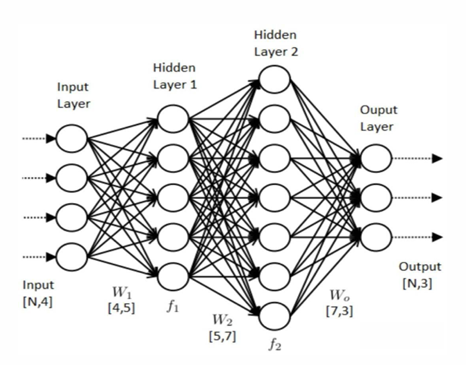
通常一个神经网络由一个 input layer（输入层），多个 hidden layer（隐藏层）和一个 output layer（输出层）构成。
图中圆圈可以视为一个神经元（感知器）。
设计神经网络的重要工作是设计 hidden layer（隐藏层），及神经元之间的权重。
添加少量隐层获得浅层神经网络；隐层很多时就是深层神经网络。

神经元 – 激活函数

在神经网络中使用激活函数的目的：引入非线性激活函数打破线性叠加的限制，解决梯度消失问题

为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：

• 连续并可导（允许少数点上不可导）的非线性函数，可以直接利用数值优化的方法来学习网络参数
• 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率
• 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效
  率和稳定性

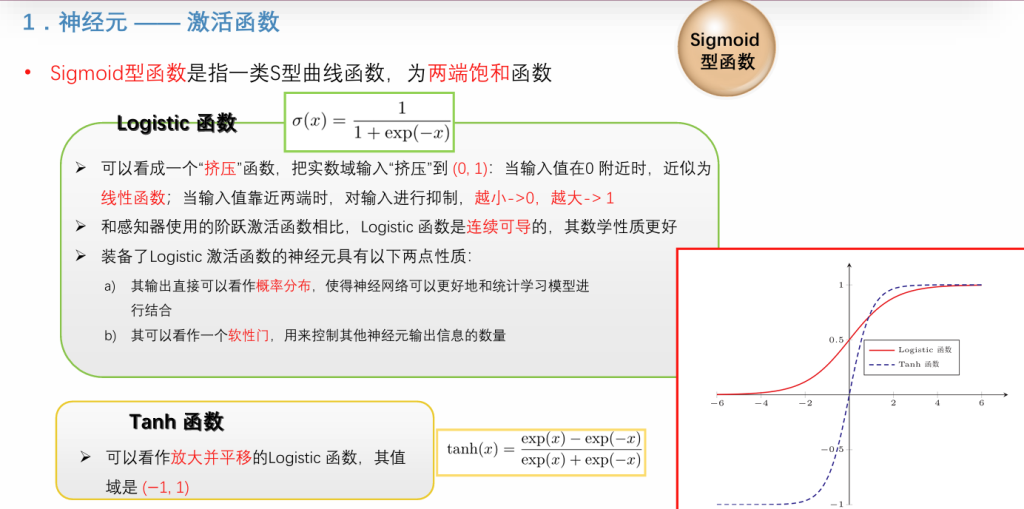
Sigmoid和Tanh

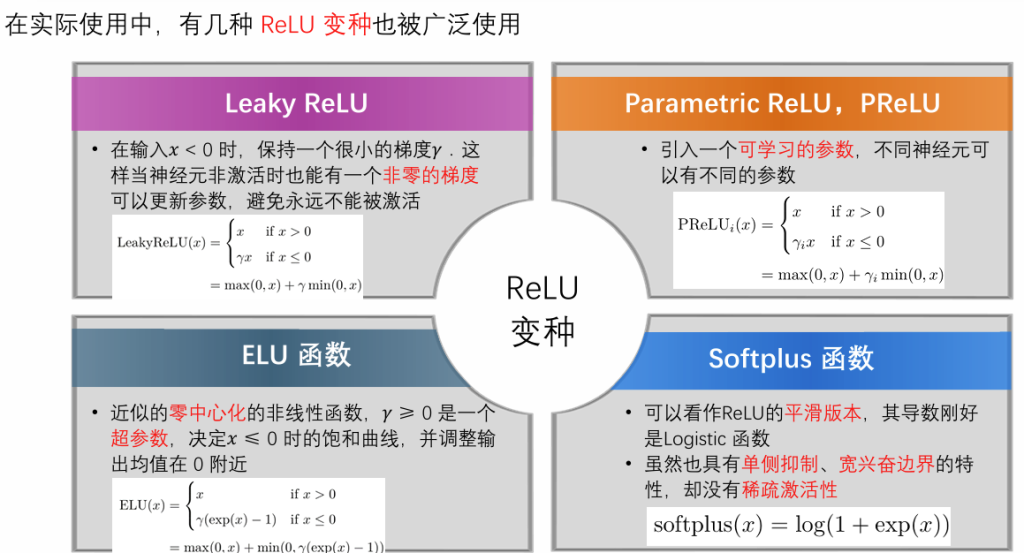
ReLU

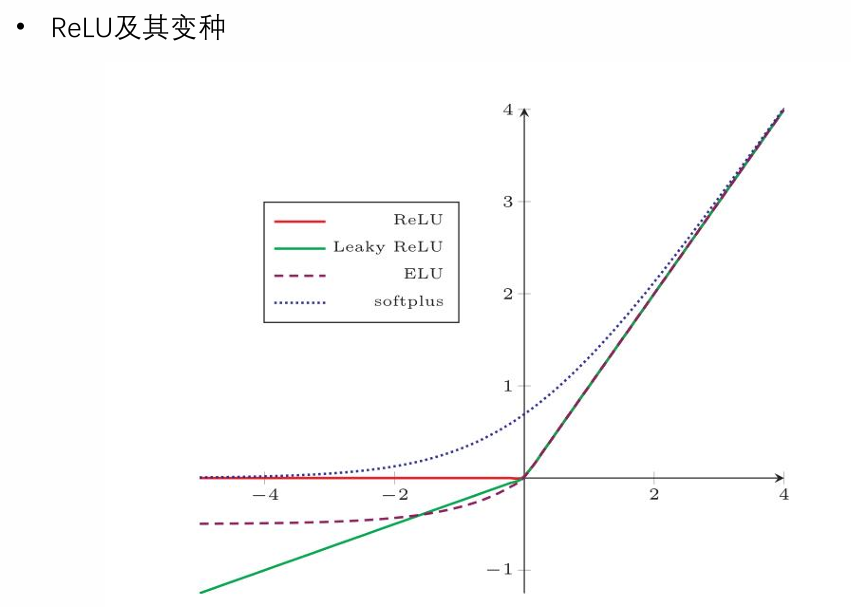
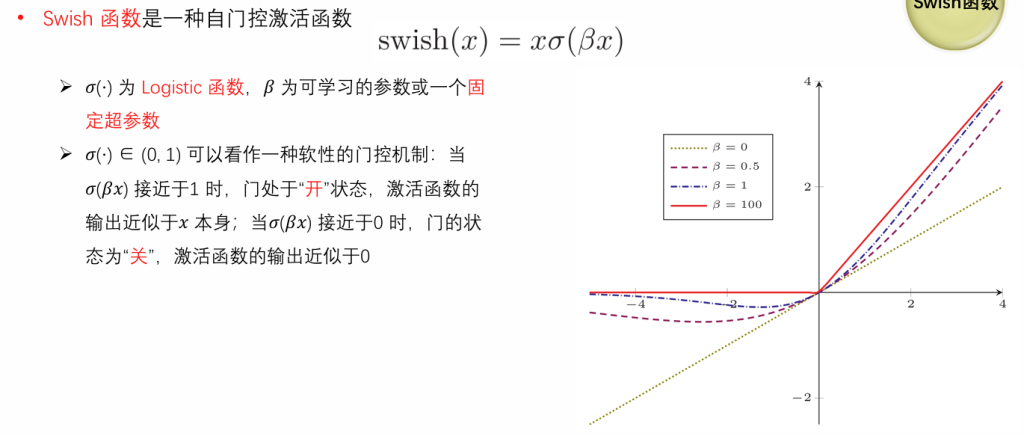
网络结构

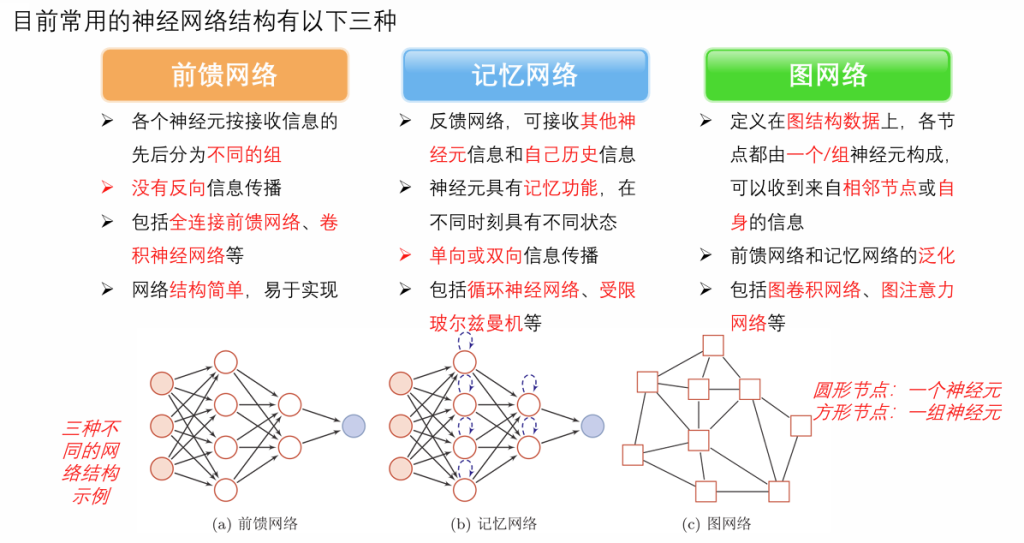
前馈神经网络

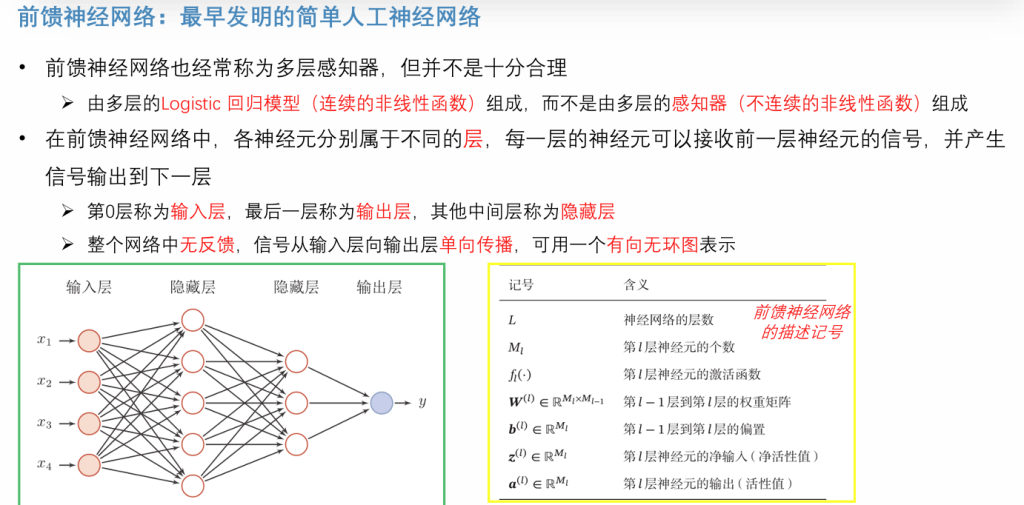
\(\boldsymbol{W}^{(l)} \in \mathbb{R}^{M_l \times M_{l – 1}}\)：即第\(l – 1\)层到第l层的权重矩阵 。其维度由前一层神经元个数\(M_{l – 1}\)和当前层神经元个数\(M_l\)决定，矩阵中的元素表示前一层神经元与当前层神经元连接的权重 。

\(\boldsymbol{z}^{(l)} \in \mathbb{R}^{M_l}\)：代表第l层神经元的净输入（净活性值） 。是由上一层输出经权重矩阵加权并加上偏置得到的，即\(\boldsymbol{z}^{(l)}=\boldsymbol{W}^{(l)}\boldsymbol{a}^{(l – 1)}+\boldsymbol{b}^{(l)}\) 。第 l层的净输入，也就是还没激活的值。

\(\boldsymbol{a}^{(l)} \in \mathbb{R}^{M_l}\)：表示第l层神经元的输出（活性值） 。是将净输入\(\boldsymbol{z}^{(l)}\)经过激活函数\(f_l(·)\)变换后得到的，即\(\boldsymbol{a}^{(l)} = f_l(\boldsymbol{z}^{(l)})\) 。第 l层的输出值（也叫“激活值”）。就是神经元最终“放出来”的信号，供下一层使用。

神经网络的一层可以简单看作“接受输入 → 加权处理 → 加偏置 → 激活输出”的过程：

每层神经网络 = 仿射变换 + 非线性变换

1. 仿射变换（Affine Transformation）是啥？
   • 就是线性变换 + 偏置项，形式为：\(\boldsymbol{z}^{(l)} = \boldsymbol{W}^{(l)}\boldsymbol{a}^{(l – 1)} + \boldsymbol{b}^{(l)}\)
   • 类比成 “线性打分” 或 “线性组合”
   • 本质是把输入数据进行一个线性压缩、旋转、平移等处理
2. 非线性变换是啥？
   • 就是激活函数的作用，如 ReLU、Sigmoid、Tanh 等：\(\boldsymbol{a}^{(l)} = \sigma(\boldsymbol{z}^{(l)})\)
   • 给网络引入 “非线性能力”，让它能学习更复杂的函数关系
   • 否则多个线性变换叠加仍然只是一个线性变换

通用近似定理：前馈神经网络具有很强的拟合能力，常见的连续非线性函数都可以用前馈神经网络来近似

神经网络作为特征转换器 + 分类器组合

我们可以把神经网络的整个过程拆成两部分：

(1) 特征提取部分（神经网络主体）：输入原始数据\(\mathbf{x}\)，经过多层网络处理，提取出一个高阶特征表示：\(\boldsymbol{\varphi}(\mathbf{x})\)（提取的特征）

(2) 分类器部分（最后一层）：用一个分类器\(g(\cdot ; \boldsymbol{\theta})\)对提取到的特征进行分类：\(\hat{y}=g(\boldsymbol{\varphi}(\mathbf{x}), \boldsymbol{\theta})\)

情况一：二分类问题（\(y \in \{0, 1\}\)）使用 Logistic 回归作为最后一层。
最后一层神经元的输出就是：\(p(y = 1|\mathbf{x})=\sigma(\boldsymbol{z}^{(L)}) = \boldsymbol{a}^{(L)}\) ，这里激活函数为 Logistic 函数（Sigmoid）。
情况二：多分类问题（\(y \in \{1, 2, \ldots, C\}\)）使用 Softmax 回归。
神经网络最后一层（第L层）设置为C个神经元。
使用 Softmax 函数做激活：\(\hat{\boldsymbol{y}}=\text{softmax}(\boldsymbol{z}^{(L)})\) ，输出为每个类别的条件概率\(p(y = c|\mathbf{x})\) 。

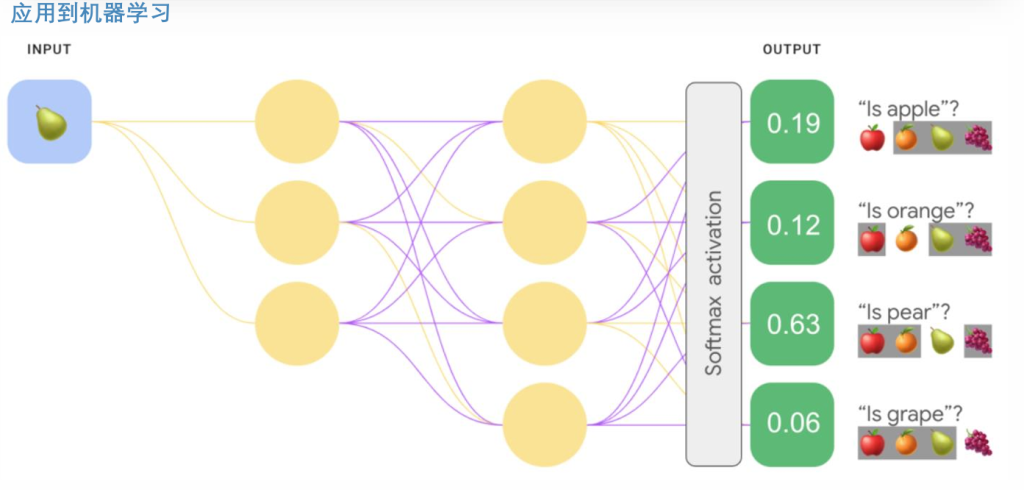
多分类例子：通过神经网络得到一个Z值，Z值输入到softmax函数中，然后会得到一个向量，该向量为该样本属于各个类的概率，因此选概率最大的0.63作为其类别
(理解过程，不用记公式)

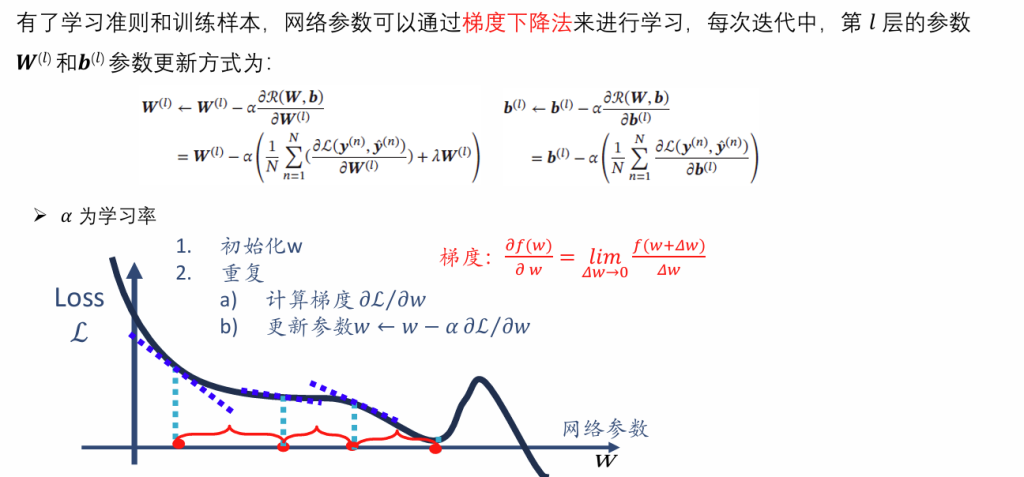
我们想求： \(\frac{\partial y}{\partial x}\),但问题是：y并不是直接由 x得来的，它是通过很多层间接传递过来的。所以我们需要“逐层地”把每一层对输入的影响都乘起来，也就是链式法则

反向传播算法

在神经网络中，当我们完成前向传播、得到了输出结果 \(\hat{y}\) 之后，为了使模型预测越来越准确，就需要不断地调整参数 \(\mathbf{W}\)、\(\mathbf{b}\)。这就需要用损失函数（Loss Function）来衡量预测结果与真实值的差距，再计算损失函数对参数的梯度进行优化更新。下面用一个例子理解过程

这是一个神经网络为了简化计算：减少隐藏层数量，删去多余的神经元和输入，暂时忽略激活函数从以下最简单的网络结构开始

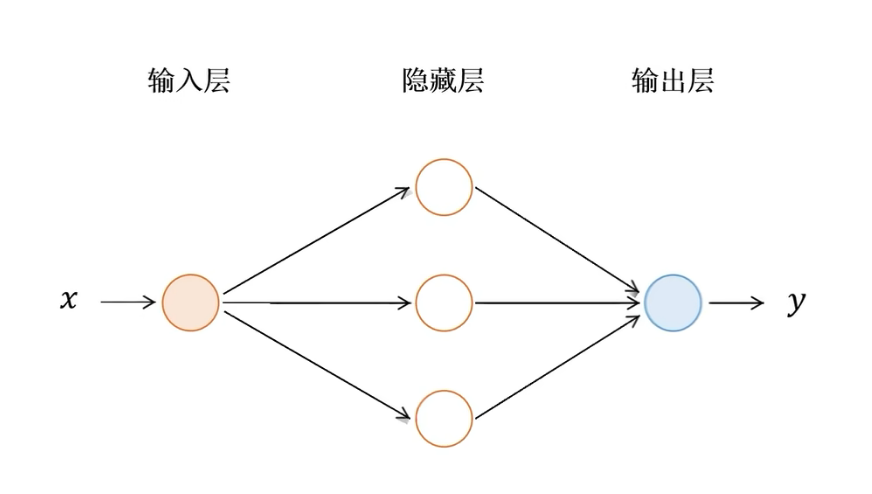
对这个神经网络标注出网络中包含的参数w，b。最终输出y和输入x之间的函数关系表达式，其中的这些参数就是我们要优化的对象

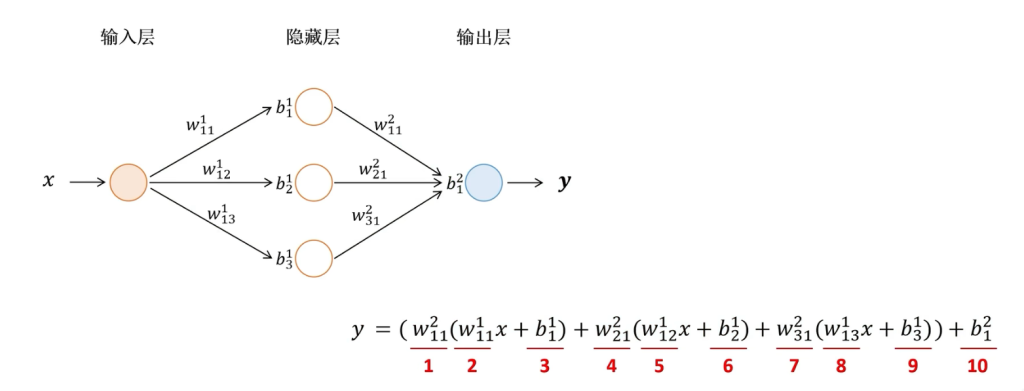
也可将各部分的计算过程分拆到每个神经元上

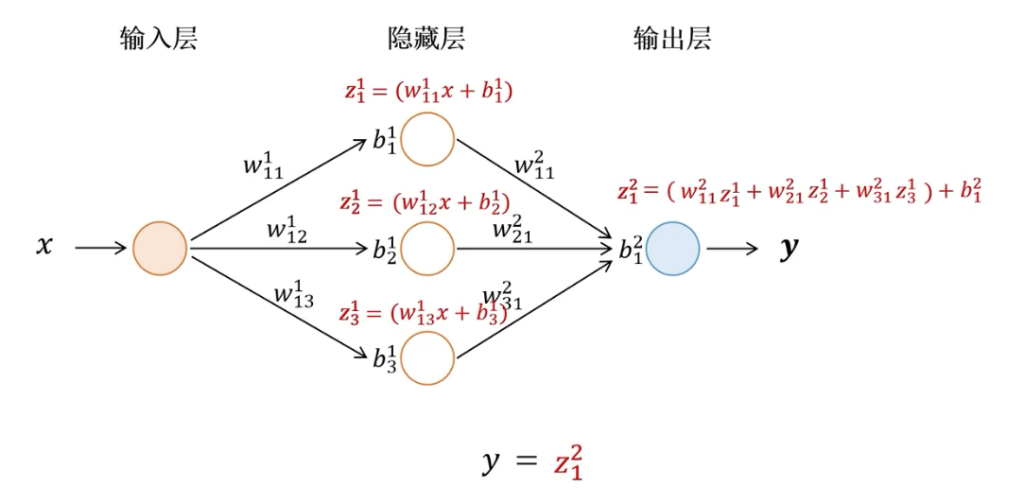
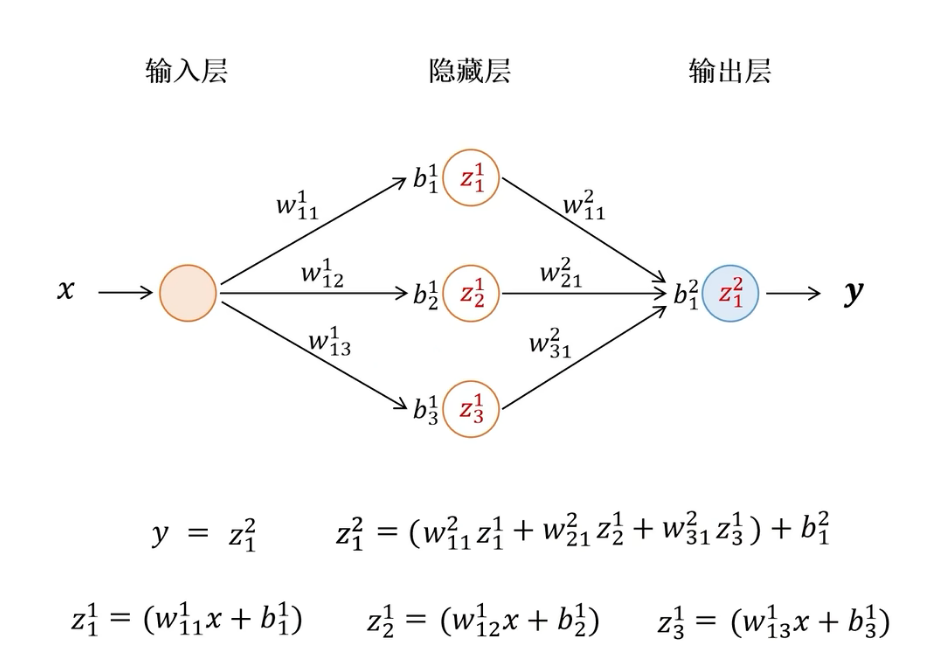
我们的目标是找到一组参数w，b使神经网络可以是输出数字2。损失函数采用输出值与期望值差的平方

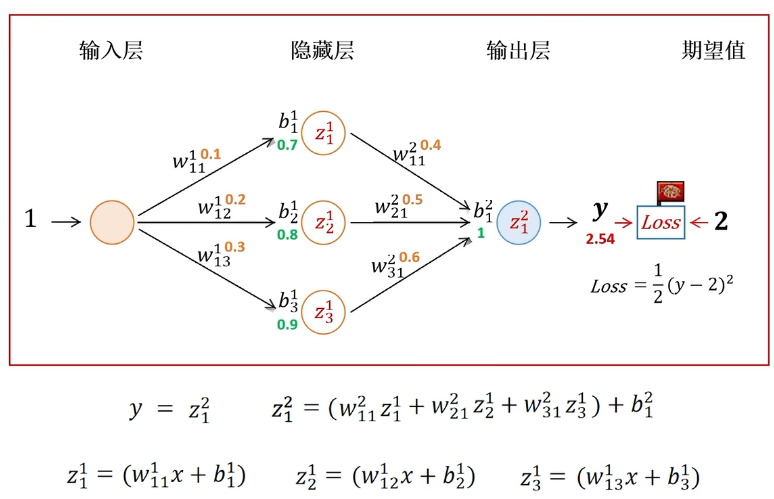
初始化一组参数w和b，求当前参数下y的输出值为2.54。下面进行反向传播，从损失函数出发，计算Loss对w11的梯度，从右向左寻找w11所在的位置，可以看到依次经过输出值y，神经元Z21，神经元Z11，因此根据链式法则从外到内的求偏导

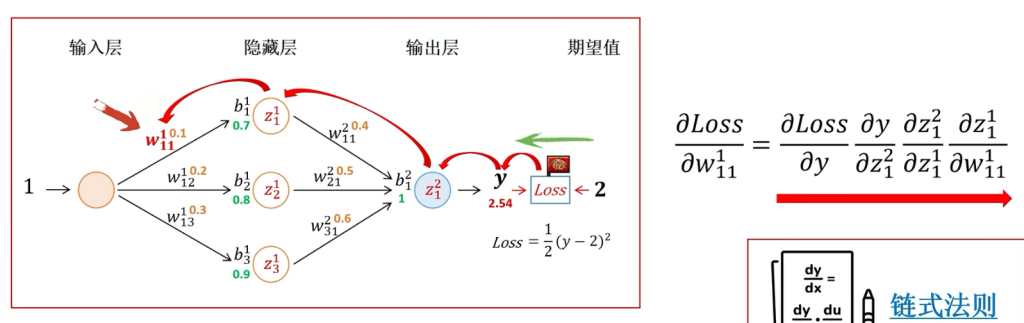
求得每一个节点的偏导数

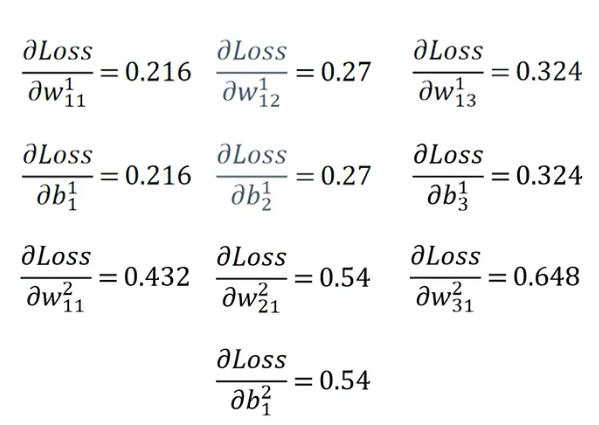
得到偏导数利用梯度下降，设学习率为0.1，更新每一个节点的权重，这样一次反向传播就完成了

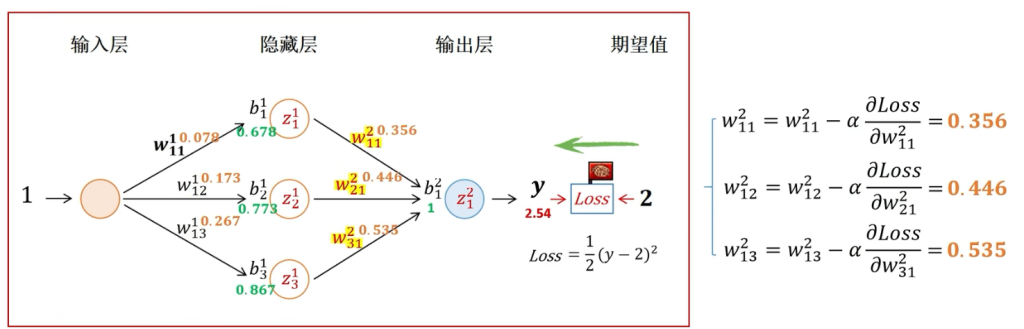
在进行前向传播(从左到右)预测误差

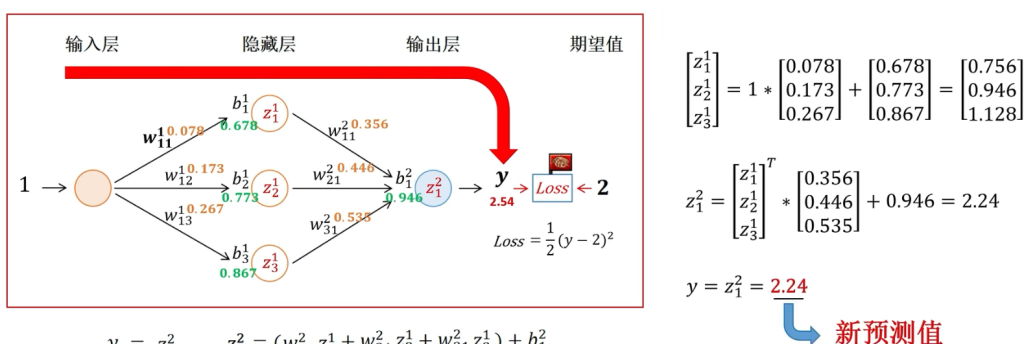
然后再以损失函数为起点，通过梯度下降更新参数，如此重复多次可以发现预测误差正在逐渐缩小

当预测误差小于规定值比如0.01时就可以停止参数更新了

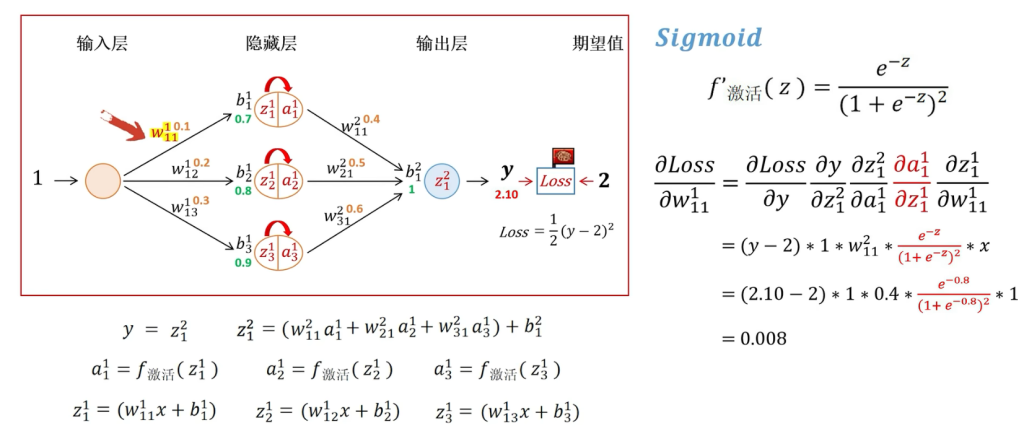
现在加入激活函数，对于可导的激活函数，直接在链式求导的过程中插入一层激活相关的偏导求解即可

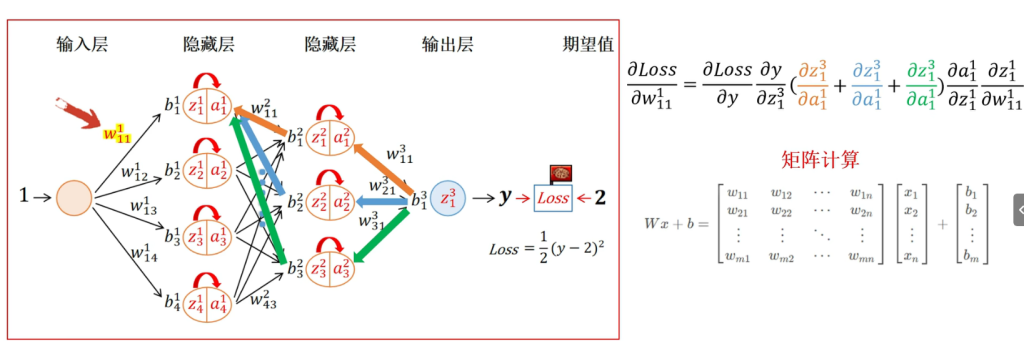
增大网络宽度，只是多乘一个偏导项。增加网络层数，对应增加链式求导的链路长度，同时由于当前神经元的数值收到上一层多个神经元输出的共同作用，通常也会用矩阵表示

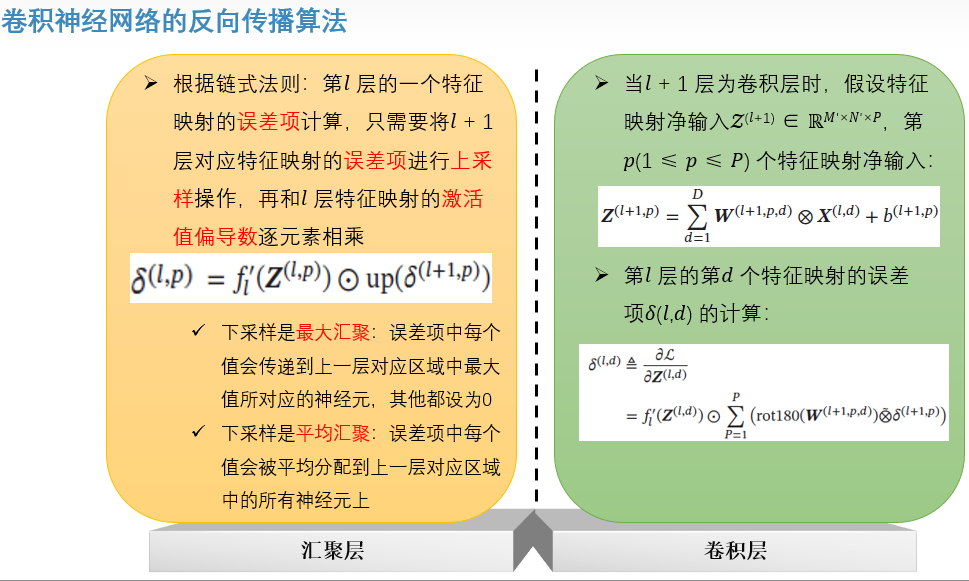
反向传播：第 𝑙 层的误差项可以通过第 𝑙 +1 层的误差项计算得到

核心数学原理：链式法则

自动梯度计算

(前两个非重点)

方法	本质	优点	缺点
数值微分	利用极限定义近似导数	直观易实现	有截断误差，不精确，计算复杂度 O(N2)O(N^2)
符号微分	解析推导表达式	精确，可用于数学变换	速度慢，不易用于循环/程序分支结构
自动微分	结合程序结构+链式法则	精确 + 高效	程序复杂时调试较难

自动梯度计算（Automatic Differentiation，简称 AD） 是一种能对程序中计算图进行链式求导的技术，核心是链式法则（Chain Rule）的程序化实现。

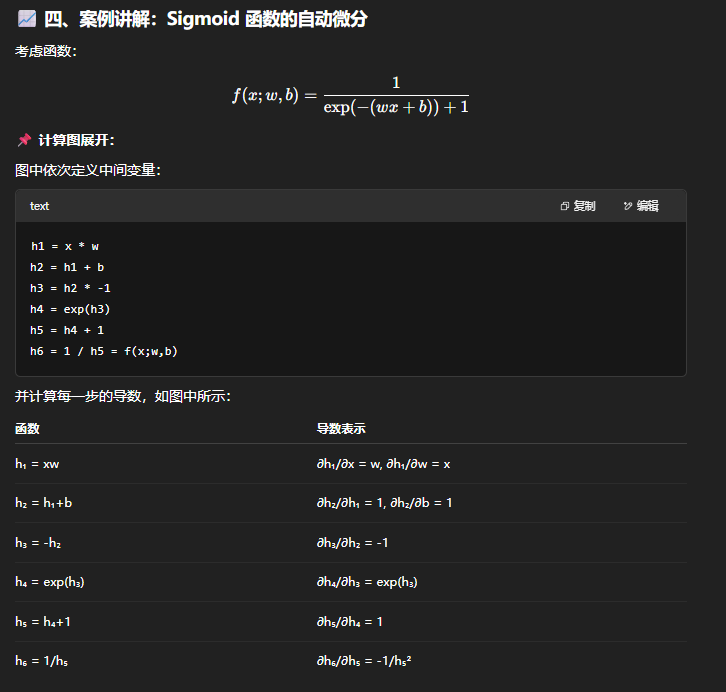
自动微分可正向传播（Forward Mode）:按计算图中计算方向的相同方向来递归地计算梯度。或反向传播：相反方向来递归地计算梯度（Reverse Mode，适合输出少输入多的情况）

对于一般的函数形式𝑓 ∶ ℝ𝑁 → ℝ𝑀，前向模式需要对每一个输入变量都进行一遍遍历，共需
要𝑁 遍，反向模式需要对每一个输出都进行一个遍历，共需要𝑀 遍。当𝑁 > 𝑀 时，反向模式
更高效

在前馈神经网络中，损失函数为：\(f: \mathbb{R}^N \to \mathbb{R}\)
即输出为一个标量（loss），输入是参数向量（维度通常很大 ）。因此：采用反向模式更高效 —— 只需一轮反向传播就能得到所有参数的梯度！

优化问题

神经网络的参数学习比线性模型要更加困难，主要原因有两点：

• 非凸优化问题：存在局部最优而非全局最优解，影响迭代
• 梯度消失问题：由于Sigmoid 型函数的饱和性，饱和区导数接近于0，当网络层数很深时，梯度会不停衰减，甚至消失，使得整个网络很难训练。下层参数比较难调。解决方式：使用导数比较大的激活函数，比如 ReLU等

卷积神经网络 Convolutional Neural Network CNN

卷积

一维卷积

[(y_t = \sum_{k = 1}^{K} w_k x_{t – k + 1}\]

可以设计不同的滤波器来提取信号序列的不同特征

• 令滤波器w=[1/K,⋯,1/K]，相当于信号序列简单移动平均（窗口大小为K）
  • 举例：如果原信号是[1, 2, 100]。你卷积得到的就是(1+2+100)/3≈34，中间的异常值 100 被拉下来了两边的小值也被拉高了
• 令滤波器w=[1,−2,1]，可以近似实现对信号序列的二阶微分
  • \(x = [2, 10, 2] \Rightarrow 2 + 2 – 2×10 = -16\)（强烈下凹），\(x = [10, 2, 10] \Rightarrow 10 + 10 – 2×2 = 16\)（强烈上凸）

二维卷积

在图像处理中，图像是以二维矩阵的形式输入到神经网络中，因此我们需要二维卷积

信号序列\(\boldsymbol{X}\)和滤波器\(\boldsymbol{W}\)的卷积：\(\boldsymbol{Y}=\boldsymbol{W}*\boldsymbol{X}\) ，\(y_{ij}=\sum_{u = 1}^{U}\sum_{v = 1}^{V}w_{uv}x_{i – u + 1,j – v + 1}\)

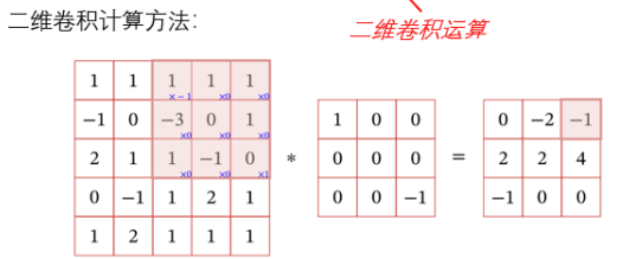
在图像处理中，卷积经常作为特征提取的有效方法，一幅图像在经过卷积操作后得到的特征的响应强度图像称为特征映射，能告诉我们“哪里有这种结构”

在图像处理中常用的均值滤波就是一种二维卷积，将当前位置的像素值设为滤波器窗口中所有像素的平均值，即 \(w_{uv}=\frac{1}{UV}\) 。

表示：

• 卷积核中每个位置的权重都是一样的
• 总共\(U×V\)个格子（比如\(3×3 = 9\)）
• 每个格子的权重是\(\frac{1}{9}\)

✅所以这个卷积核长这样（以\(3×3\)为例）： \(\text{Kernel}=\begin{bmatrix}\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\\\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\\\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\end{bmatrix}\)

✅具体含义是： 对图像中每一个像素点，执行如下操作：

1. 把它和它周围一圈像素（比如共 9 个）抽出来
2. 把这 9 个数求平均（每个乘\(\frac{1}{9}\) ）
3. 得到的新值，作为这个像素在输出图中的值

互相关

不翻转卷积。通常在在机器学习和图像处理领域，以互相关操作来代替卷积，减少一些不必要的操作或开销

步长和零填充

在卷积的标准定义基础上，还可以引入卷积核的滑动步长和零填充来增加卷积的多样性，可以更灵活地进行特征抽取

• 步长Stride：卷积核在滑动时的时间间隔
• 零填充Padding：在输入向量两端进行补零

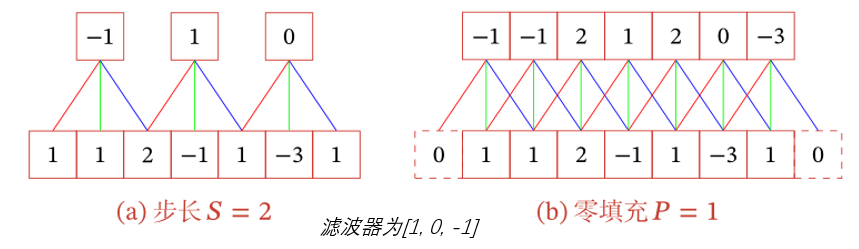
注意不是通过修改卷积核使某些项为0实现步长的，而是最初始的途径：改变滑动时的格数

零填充后的神经元数量

卷积的输出即卷积层的神经元

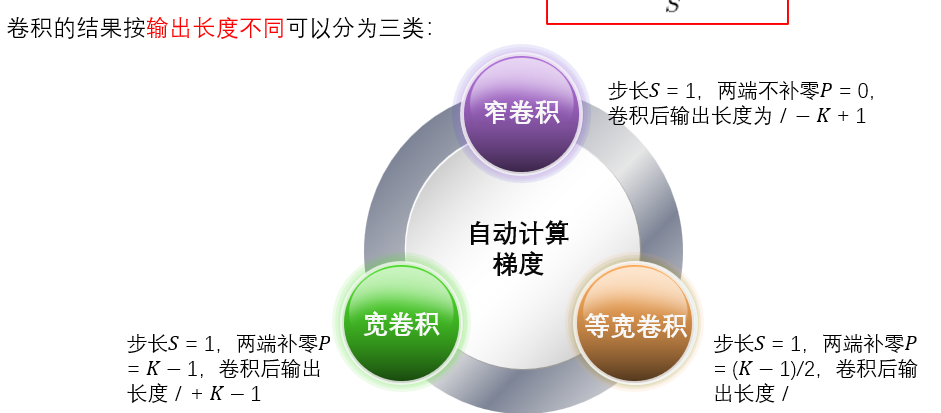
1. 窄卷积（Valid Convolution）

✅设置：

• 输入：1,2,3,4,5，长度\(I = 5\)
• 卷积核：1, 0, -1，长度\(K = 3\)
• 步长\(S = 1\)，不补零\(P = 0\)

✅输出长度： \(O=I – K + 1=5 – 3 + 1 = 3\)

✅实际卷积过程： 滑动窗口覆盖：

• \([1,2,3]\to1×1 + 0×2+(-1)×3=-2\)
• \([2,3,4]\to2×1 + 0×3+(-1)×4=-2\)
• \([3,4,5]\to3×1 + 0×4+(-1)×5=-2\)

✅输出： \([-2,-2,-2]\)

2. 等宽卷积（Same Convolution）

✅设置：

• 同样的输入：1,2,3,4,5
• 卷积核：1, 0, -1
• 步长\(S = 1\)
• 补零\(P=\frac{K – 1}{2}=1\)

✅补零后输入： [0,1,2,3,4,5,0]

✅输出长度： \(O = I = 5\)

✅实际卷积过程： 滑动核 5 次，得到：

• [0,1,2] → -1
• [1,2,3] → -2
• [2,3,4] → -2
• [3,4,5] → -2
• [4,5,0] → -1

✅输出： [-1,-2,-2,-2,-1]

3. 宽卷积（Full Convolution）

✅设置：

• 输入：1,2,3,4,5
• 卷积核：1, 0, -1
• 步长\(S = 1\)
• 补零\(P = K – 1 = 2\)

✅补零后输入： [0,0,1,2,3,4,5,0,0]

✅输出长度： \(O = I + K – 1 = 5 + 3 – 1 = 7\)

✅实际卷积过程： 滑动 7 次，得到：

• [0,0,1] → 1
• [0,1,2] → 1
• [1,2,3] → -2
• [2,3,4] → -2
• [3,4,5] → -2
• [4,5,0] → -1
• [5,0,0] → 5

✅输出： [1,1,-2,-2,-2,-1,5]

证明

输入图像X：比如一张图片，大小是\(M×N\)
卷积核W：比如一个\(3×3\)的特征提取模板，大小\(U×V\)
输出特征图\(Y = W \otimes X\)：是卷积结果，大小为\((M – U + 1)×(N – V + 1)\)

其他卷积形式

转置卷积

将低维特征映射到高维特征的卷积操作，也称为反卷积

无论是全连接网络还是卷积网络，前向传播和反向传播之间都存在结构上的“转置关系”，这在反向传播算法中尤为关键。

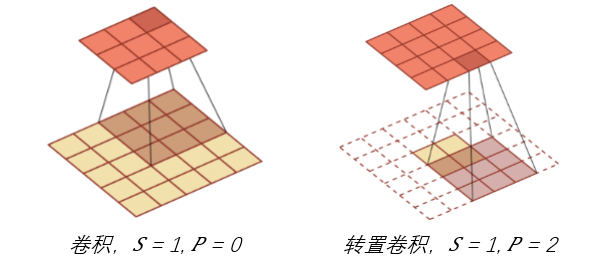
微步卷积

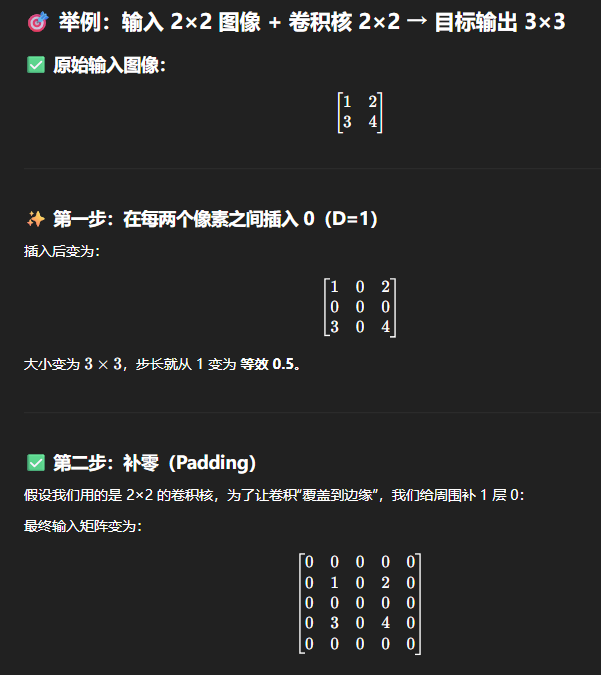
正常卷积中常用的步长 S 是 1、2、3 等整数，表示卷积核滑动时每次跨几格。但有时我们希望上采更细致，例如比原图分辨率更高怎么办？

步长为 S<1 的卷积在数学上不好直接实现，因此使用“插 0 的方式”间接模拟出“更小步长”的效果。

举例来说，如果你希望步长从 1 降为 0.5，那么你需要在原数据中每两个元素之间插入一个 0。

空洞卷积

一种不增加参数数量， 同时增加输出单元感受野的一种方法，也称为膨胀卷积

感受野：指的是一个输出单元“能看到”的输入区域的大小。感受野越大，意味着神经网络越能捕捉“远距离”的信息

如何扩大感受野

方法	效果	缺点
① 增大卷积核大小	感受野变大	参数也变多
② 增加卷积层数	类似大卷积核效果	网络更深，信息更复杂
③ 使用池化汇聚操作	感受野变大	信息会丢失（不精准）

空洞卷积是一种更聪明的做法：“插空洞”来变相增大卷积核尺寸，但不增加参数！

膨胀率 D：在卷积核的元素之间插入空洞的间隔大小

K 个元素 ⇒ 有 K−1个间隔，相邻元素之间的距离是K = (K-1)D+1（也可写为𝐾′ = 𝐾 + (𝐾 − 1) × (𝐷 − 1)）

卷积层

性质

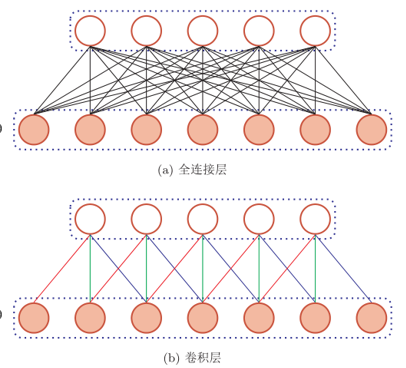
• 局部连接：在卷积层中的每一个神经元都只和下一层中某个局部窗口内的神经元相连，构成一个局部连接网络
  • 卷积层和下一层之间的连接数大大减少，由原来的\(M_l×M_{l – 1}\)个连接变为\(M_l×K\)个连接，K为卷积核大小
• 权重共享：作为参数的卷积核\(w(l)\)对于第l层的所有的神经元都是相同的
  • 所有的同颜色连接上的权重是相同的
  • 可理解为一个卷积核只捕捉输入数据中一种特定的局部特征，如果要提取多种特征就需要使用多个不同的卷积核

由于局部连接和权重共享，卷积层的参数只有一个K维的权重\(w(l)\)和 1 维的偏置\(b(l)\)，共\(K + 1\)个参数（参数个数和神经元的数量无关）

作用

作用：提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器

• 为了更充分地利用图像局部信息，通常将神经元组织为三维结构的神经层，其大小为高度M× 宽度N× 深度D，由D个M×N大小的特征映射构成
• 特征映射（Feature Map）：一幅图像（或其他特征映射）在经过卷积提取到的特征，每个特征映射可以作为一类抽取的图像特征
  • 为了提高卷积网络的表示能力，可以在每一层使用多个不同的特征映射，以更好地表示图像的特征
  • 在输入层，特征映射就是图像本身。如果是灰度图像，就有一个特征映射，输入层的深度\(D = 1\)；如果是彩色图像，有 RGB 三个颜色通道的特征映射，输入层的深度\(D = 3\)

通用结构(非重点，目前不是很明白）

输入特征映射组：\(\mathcal{X} \in \mathbb{R}^{M \times N \times D}\)为三维张量，其中每个切片矩阵\(\boldsymbol{X}^d \in \mathbb{R}^{M \times N}\)为一个输入特征映射，\(1 \leq d \leq D\)；
输出特征映射组：\(\mathcal{Y} \in \mathbb{R}^{M^\prime \times N^\prime \times P}\)为三维张量，其中每个切片矩阵\(\boldsymbol{Y}^p \in \mathbb{R}^{M^\prime \times N^\prime}\)为一个输出特征映射，\(1 \leq p \leq P\)；
卷积核：\(\mathcal{W} \in \mathbb{R}^{U \times V \times P \times D}\)为四维张量，其中每个切片矩阵\(\boldsymbol{W}^{p, d} \in \mathbb{R}^{U \times V}\)为一个二维卷积核，\(1 \leq p \leq P\)，\(1 \leq d \leq D\)。

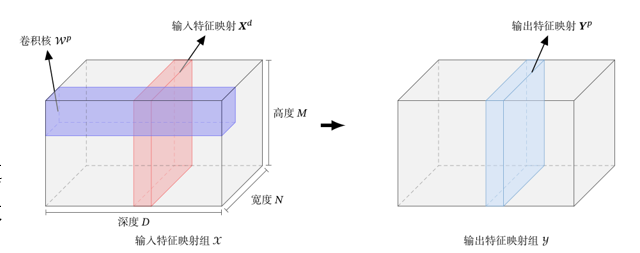
三者的关系：输入特征，经过卷积核就是一组和输入特征通道数对齐的小窗口，不断在 H×WH×WH×W 平面上滑动，通过“权重×输入”再求和的方式，把输入特征映射成新的特征图。

输入：比如一张 256×256 的 RGB 图像（\(D = 3\)）。
卷积操作：用 64 组不同的 3×3×3 的卷积核去扫描图像，每组生成一个特征图。
输出：得到 64 张 254×254 的特征图（假设无填充，步长 = 1），每张代表某种特征（如边缘、纹理、颜色分布等 ）

计算过程(重点)

为了计算输出特征映射𝒀𝑝，用卷积核𝑾^𝑝,1, 𝑾^𝑝,2, ⋯ , 𝑾^𝑝,𝐷 分别对输入特征映射𝑿¹, 𝑿², ⋯ , 𝑿^𝐷 进行卷积，然后将卷积结果相加，并加上一个标量偏置𝑏得到卷积层的净输入𝒁^𝑝， 再经过非线性激活函数后得到输出特征映射𝒀^𝑝

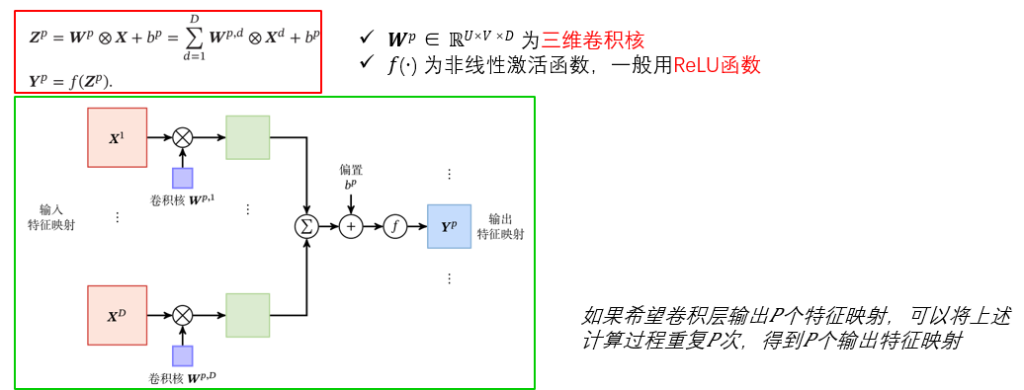
看不懂？没关系，请看下面的例子，原视频链接，讲的真的很好09.卷积层的介绍_哔哩哔哩_bilibili

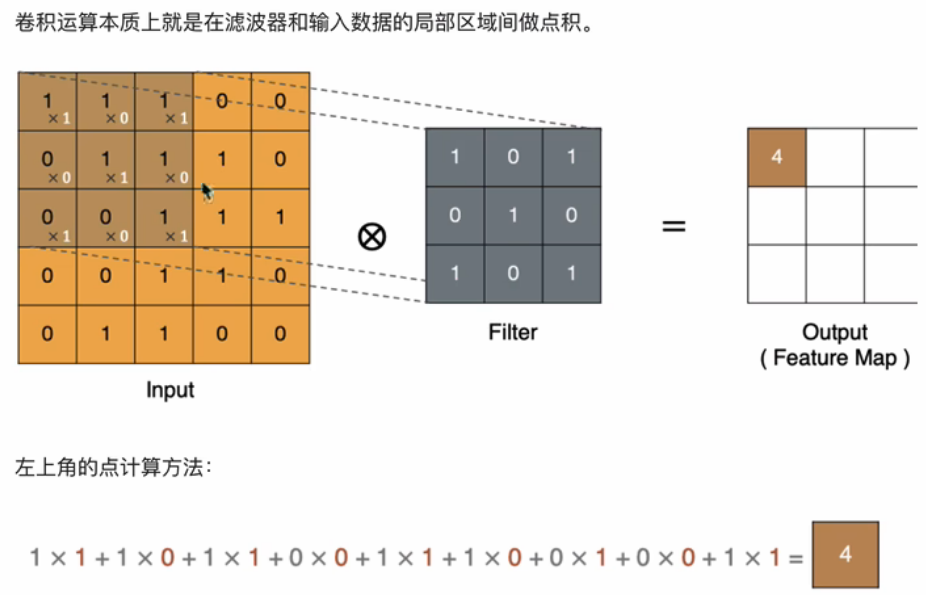
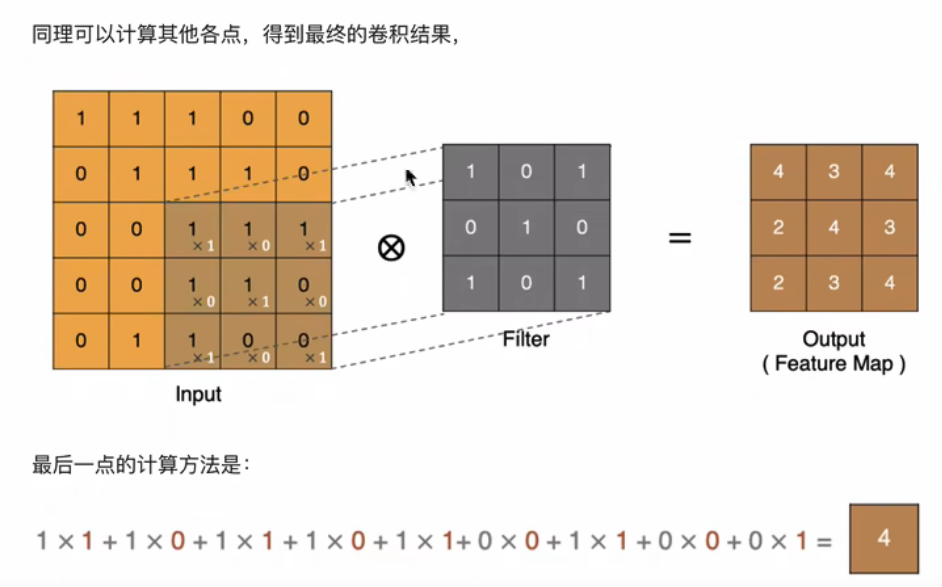
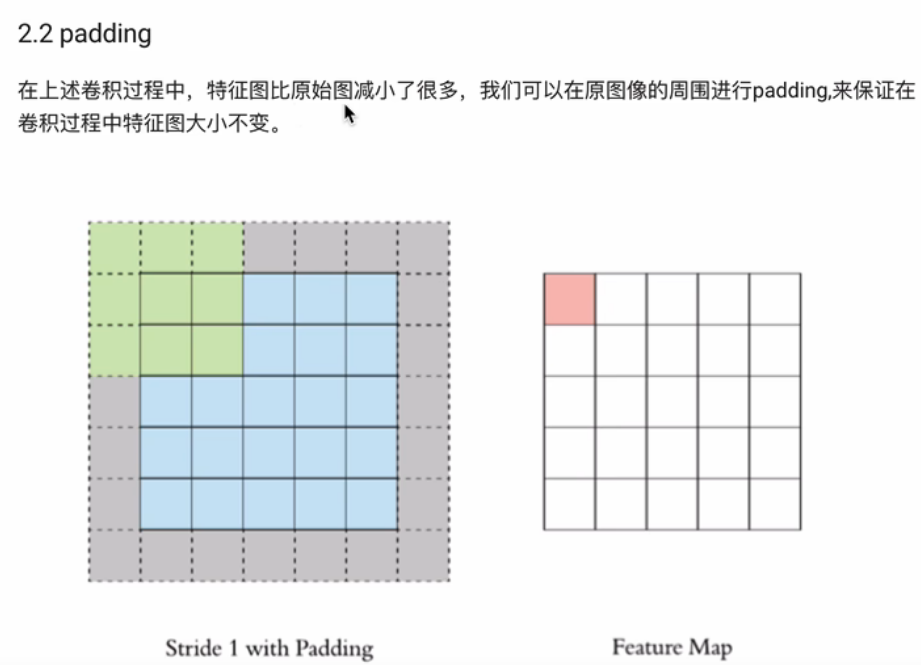
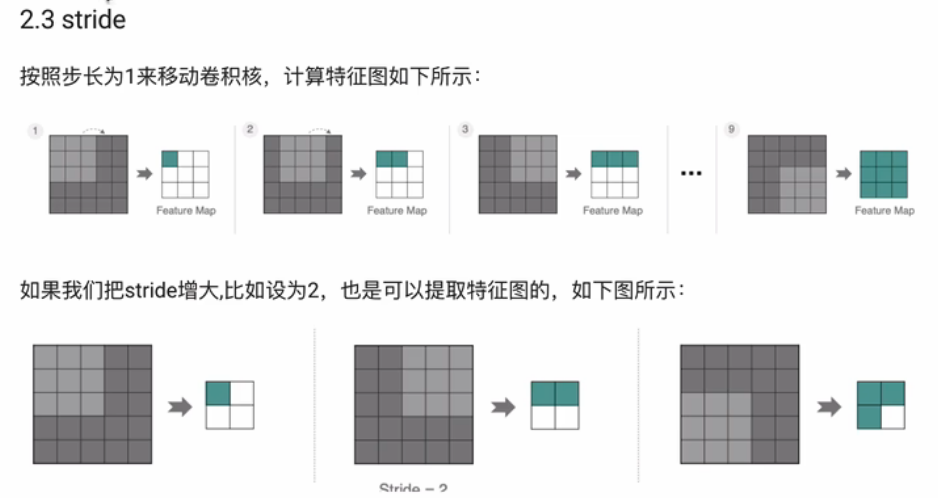
当原来5×5的通道不再是单通道，而是3通道时，此时也需要将卷积核变为3通道，卷积核的3个通道分别与对应的输入通道进行上述的卷积操作。然后再将每个卷积得到的结果求和才能得到特征图，详情见下

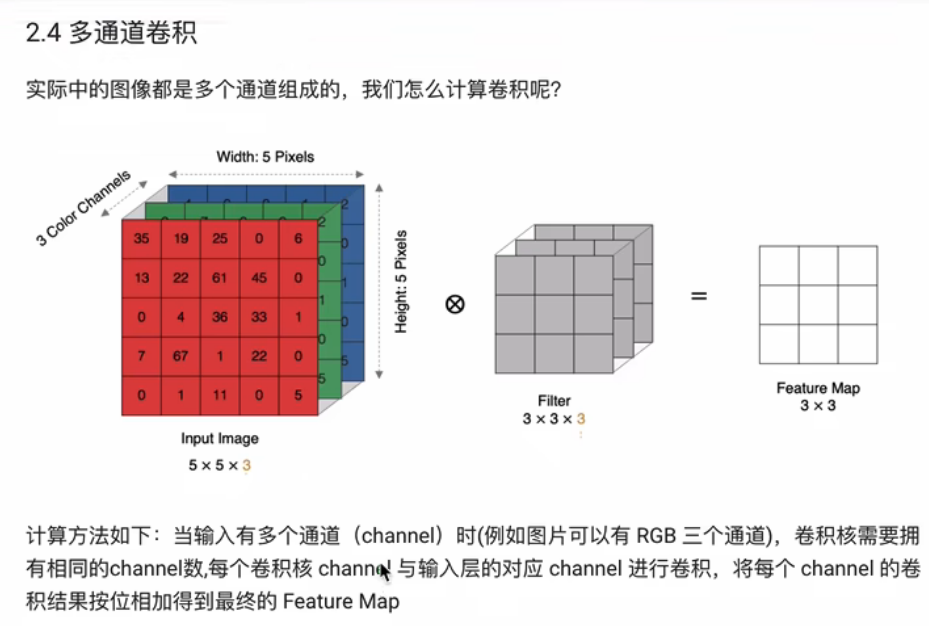
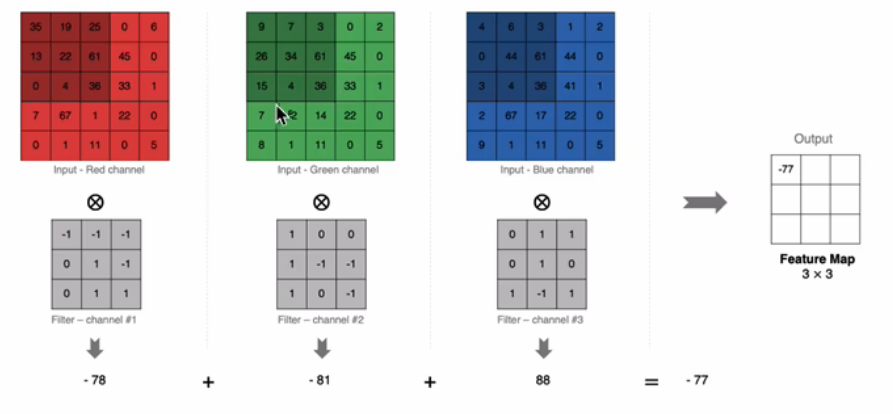
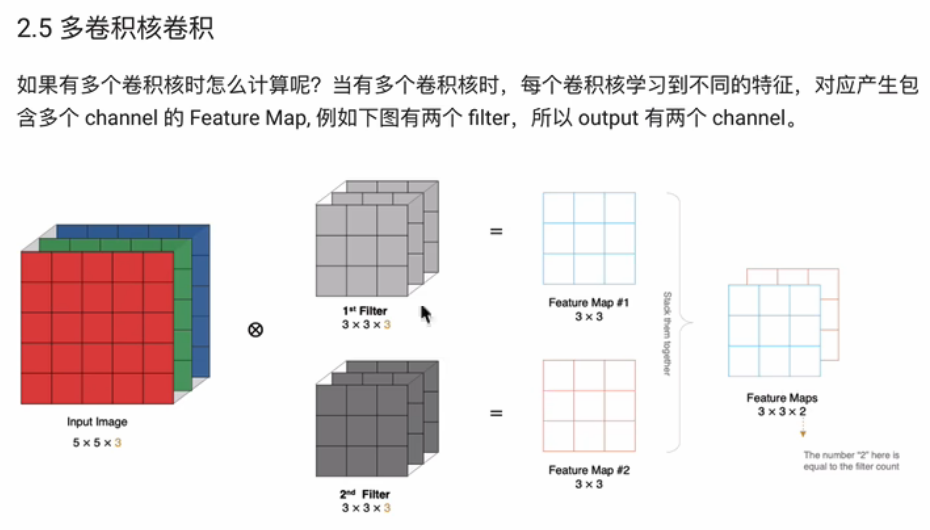
D1是输入特征图的通道数，K卷积核元素的个数，F卷积核的大小指n×n的，零填充大小是指再特征图周围填充的个数

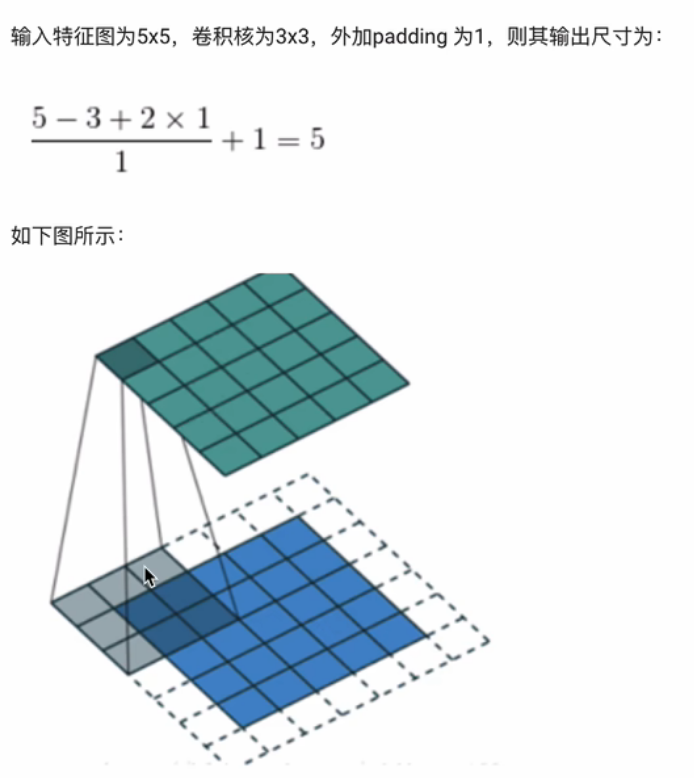
注：输入特征图-蓝，通道数为1。卷积核-灰，通道数为1。输出特征图-绿，通道数为1

汇聚层（Pooling，池化）

也叫子采样层，其作用是进行特征选择，降低特征数量，从而减少参数数量

• 卷积层虽然可显著减少网络中连接的数量，但特征映射组中的神经元个数并没有显著减少，如果后面接一个分类器，其输入维数依然很高，很容易出现过拟合。
• 可以在卷积层之后加上一个汇聚层，从而降低特征维数，避免过拟合
  • 汇聚：指对每个区域进行下采样得到一个值，作为这个区域的概括。常用的汇聚函数有两种：最大汇聚和平均汇聚

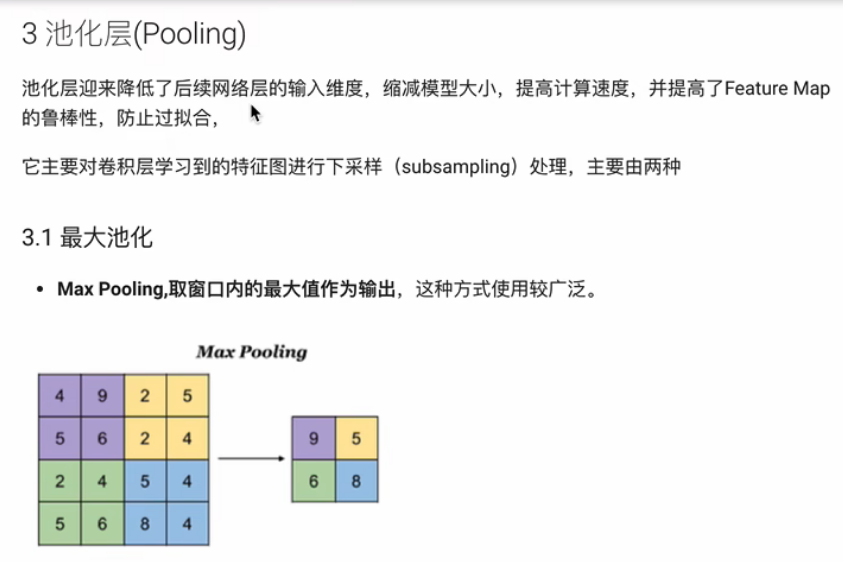
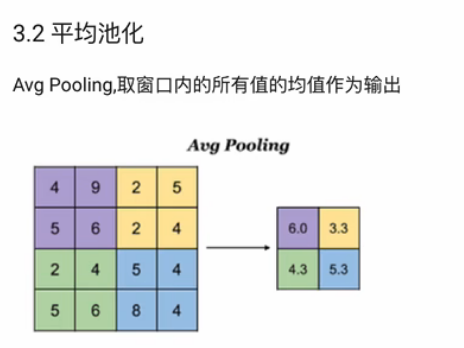
全连接层

CNN 事实上是通过卷积自动的学习到了数据的特征，再将这些特征转为一维空间的特征向量，使用传统的神经网络进行分类

全连接层就是传统的神经网络，全连接这个词表明前面层的所有神经元都与下一层的所有神经元连接，这就是传统神经网络的连接方式。

卷积网络的整体结构

卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成

• 卷积网络整体结构
  • 一个卷积块为连续M个卷积层和b个汇聚层（M通常设置为 2~5，b为 0 或 1）
  • 一个卷积网络中可以堆叠N个连续的卷积块，然后在后面接着K个全连接层（N的取值区间比较大，比如 1~100 或者更大；K一般为 0~2）

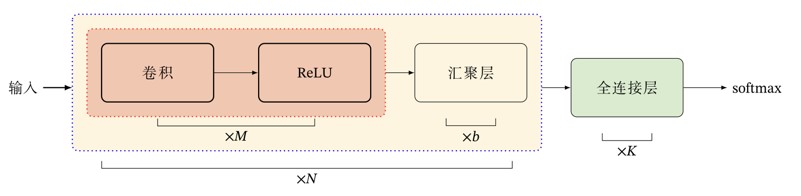
• 卷积网络的整体结构趋向于： a) 使用更小的卷积核（比如\(1 \times 1\)和\(3 \times 3\)）及更深的结构（比如层数大于 50） b) 目前比较流行的卷积网络中，汇聚层的比例正在逐渐降低，趋向于全卷积

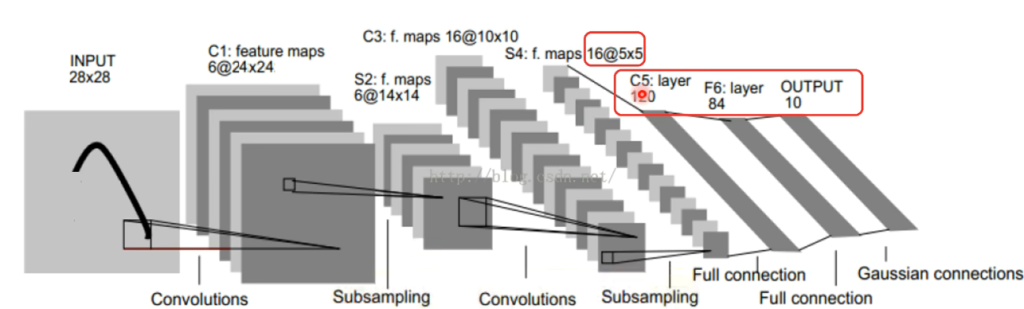
C1：用6个卷积核对二维图像卷积，得到了6个不同的二维特征图像

S2：做池化使特征图像分辨率变小

C3，用更多的卷积核获取更多的16个特征图像

S4：再次进行池化，生成16个五×五的小图像

C5：如果要进行全连接，需要将这些特征图像按照顺序拉伸到一维空间并进行合并，16@5×5 就有 16x5x5 = 400 个像素点。组成一个一维的特征向量，有 400 个特征，对应 400 个神经元最后变成一维图像，中间有2个隐含层分别有120和·84个神经元，最后输出10个神经元代表10个输出结果，即0-9的概率，谁的概率最高就认为是哪个图像

参数学习

在卷积网络中，参数为卷积核中权重以及偏置

和全连接前馈网络类似，卷积网络也可通过误差反向传播算法来进行参数学习

在全连接前馈神经网络中，梯度主要通过每一层的误差项𝛿 进行反向传播，并进一步计算每层参数的梯度

在卷积神经网络中，主要有两种不同功能的神经层：卷积层和汇聚层，而参数为卷积核以及偏置，因此只需要计算卷积层中参数的梯度

在卷积网络中，每层参数的梯度依赖其所在层的误差项 𝛿(𝑙,𝑝)